ESDEP WG 10
COMPOSITE CONSTRUCTION
To describe the basic behaviour of composite beams including a geometric description of a typical beam, its construction, and the stress strain relationships that develop under load.
Lecture 7.8.2: Restrained Beams
Lecture 10.1: Composite Construction - General
Lecture 10.3: Single Span Beams
Lectures 10.4: Continuous Beams
Lectures 10.5: Design for Serviceability
Lectures 10.6: Shear Connection
Composite beams are described in terms of the steel section, concrete slab and connectors used in a typical building floor. The material behaviour of each of the components is briefly reviewed and reference is made to the slender nature of the steel section and the anisotropic nature of the concrete slab. The structural behaviour of a typical composite beam is described, in three stages, by reference to the strain and stress in each component part. Firstly at low loads when full interaction and a linear elastic response occurs; secondly as slip takes place with increasing load, and finally as the materials reach failure stresses. Propped and unpropped construction gives rise to different beam behaviour which is described. Partial interaction is also explained in qualitative terms. The lecture concludes with a summary of the constraints that the engineer must take into account when designing composite beams.
This lecture outlines, in general terms, the behaviour of the most common form of composite element - the composite beam. In doing this it will be possible to explain many of the problems associated with the analysis and design of other elements such as columns and slabs. The lecture therefore forms a basis on which to build an understanding of composite behaviour.
A general description of a composite beam is followed by a more detailed discussion the component parts and their individual structural behaviour. The structural action is described by reference to the strain, and resulting stress, history of a typical composite beam as it deforms, under increasing load, to failure.
The way in which composite beams are constructed may alter their resistance to applied loads. Consequently it is essential to design composite beams for both the construction and in-service condition. It is also possible to design a beam for "partial connection" so that each condition is equally critical. A definition of partial connection, and brief reasons for the two-stage design requirement, is described. Simple single spans are a common form of beam and their behaviour is explained. The behaviour of continuous spans is also introduced.
Finally, a summary of the design criteria for composite beams is given. These criteria are covered in more detail in subsequent lectures.
Since a composite beam is formed from three components, see Figure 1, it is necessary to review the behaviour of each before describing the overall behaviour of the combination.

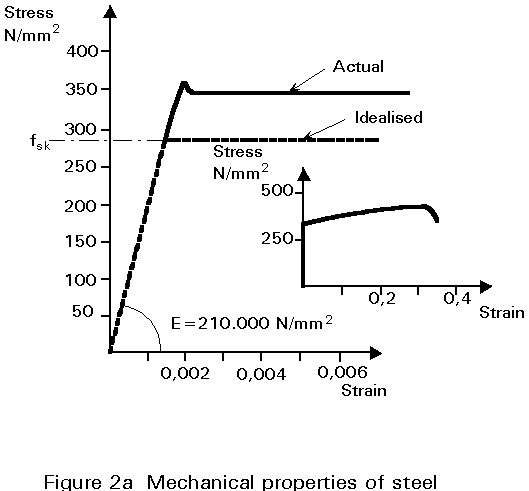
Under both tension and compression, steel behaves in a linearly elastic fashion until first yield of the material occurs. Thereafter it deforms in a perfectly plastic manner until strain hardening occurs. This behaviour is shown diagrammatically in Figure 2a together with the idealisation of steel behaviour which is assumed for design. In general, most of the steel section is in tension for simple sagging bending and local buckling of slender sections is not a problem. However, for continuous beams, significant parts of the steel section are subject to compression and local buckling has to be considered. This topic will be covered in Lecture 10.4.1 and 10.4.2.
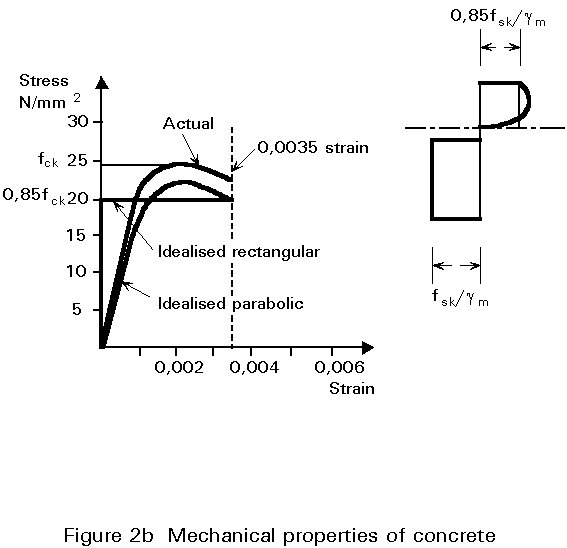
The behaviour of concrete is more complex. Two situations have to be considered. Concrete in compression follows a non-linear stress/strain curve. This behaviour is shown in Figure 2b together with the two idealisations used in design. The parabolic stress block is often used in reinforced concrete design but the rectangular block is normally assumed in composite beam design. The non-linear material behaviour gives rise to an inelastic response in the structure. Concrete in tension cracks at very low loads and it is normally assumed, in design, that concrete has no tensile strength.
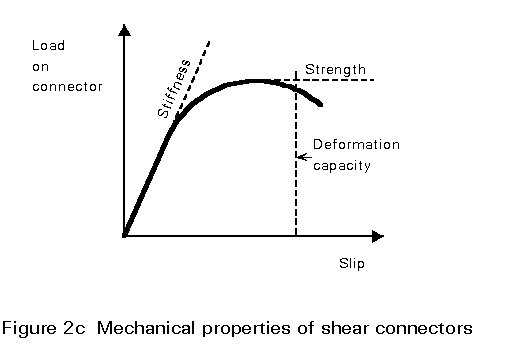
The connection behaviour, see Figure 2c, will be covered in detail in Lecture 10.6.1. It is sufficient, here, to say that it is also non-linear. This behaviour adds to the complexity of design.
Composite beams are formed with a solid, composite or precast concrete slab spanning between, and connected to, the steel sections. Figure 1 shows a typical layout. The steel parts are often confusingly referred to as the "beams". In this lecture they are called "steel sections" to avoid confusion .
The slab usually spans between parallel steel sections and its design is normally dictated by this transverse action. Consequently the span, depth and concrete grade are determined separately and are known prior to the beam design.
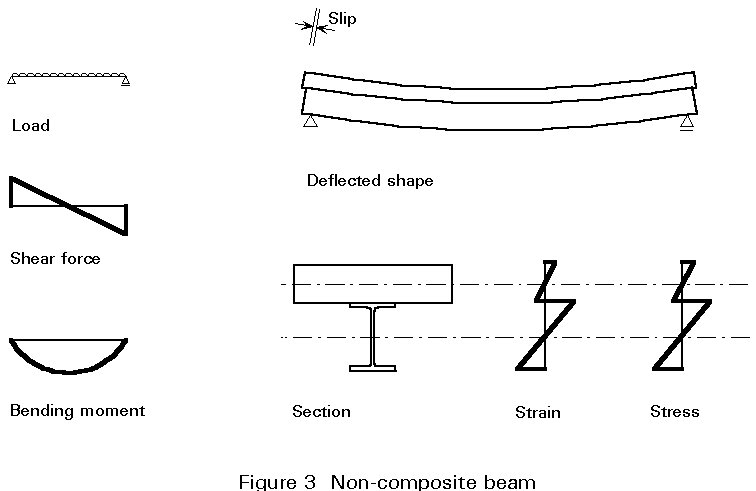
For non-composite construction, the steel sections alone are designed to carry the load acting on the floor plus the self weight of the slab, as shown in Figure 3. The steel section is symmetric about its mid depth and has a neutral axis at this point. The section strains around this neutral axis and both the outer fibre tensile and compressive stresses are identical. The stresses (s) in tension (t) and in compression (c) in the steel section may be evaluated using simple bending theory.
st and sc = Mservice load / Wsteel section
The concrete slab is not connected to the steel section and therefore behaves independently. As it is generally very weak in longitudinal bending it deforms to the curvature of the steel section and has its own neutral axis. The bottom surface of the concrete slab is free to slide over the top flange of the steel section and considerable slip occurs between the two. The bending resistance of the slab is often so small that it is ignored.
Alternatively, if the concrete slab is connected to the steel section, both act together in carrying the service load as shown in Figure 4. Slip between the slab and steel section is now prevented and the connection resists a longitudinal shear force similar in distribution to the vertical shear force shown.
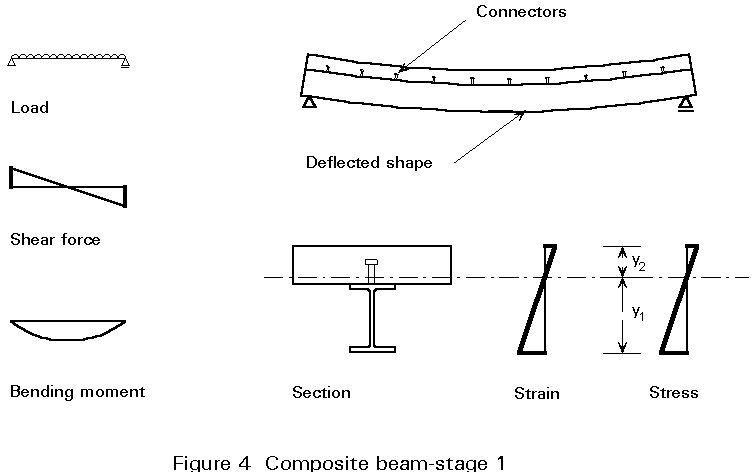
The composite section is non-symmetric and shown a single neutral axis often close to the top flange of the steel section. The tensile and compressive stresses at the outer fibres are therefore dependent upon the overall moment of inertia (I) of the composite section and their distance from the single neutral axis.
Assuming that the loading causes elastic deformation the stresses generated in the section may be determined using simple bending theory. The stresses for the service load condition may be obtained (Figure 4) from:
st = Mservice load * y1 / Icomposite section
sc = Mservice load * y2 / Icomposite section
where
y1 is the distance of the extreme steel fibre from the neutral axis
y2 is the distance of the extreme concrete fibre from the neutral axis
The I value of the composite section is normally several times that of the steel section. It can therefore be seen that, for a similar load, the extreme fibre stresses generated in the composite section will be much smaller than those generated in the non-composite beam.
This difference also has an effect on the stiffness of the beams which will be discussed in more detail in Lectures 10.5.1 and 10.5.2.
The stresses developed in the slab as it spans transversely to the length of the beam are assumed not to affect the longitudinal behaviour. They are generally ignored when designing the composite beam. However the span of the beam often dictates how much of the slab may be assumed to help in the longitudinal bending action. This assumption will be covered in more detail in Lecture 10.3. Here half the transverse span, each side of the steel section, is assumed to be effective in carrying the longitudinal compression.
The connection between the slab and steel section may be made in many ways. In general it is formed using a series of discrete mechanical keys. The most common form of connector is the headed stud which is shown in Figure 1. Lecture 10.6.1 and 10.6.2 cover the detailed behaviour of this connector and also describe several other types.
It can be seen that composite beams form part of a complex flooring system and it is difficult to separate the transverse and longitudinal actions of the slab. Figure 1 identifies the typical beam section which is discussed in the remainder of this lecture.
The way in which a composite beam behaves under the action of low load, medium load and the final failure load is best described in stages. The load, the bending moment and shear force diagrams, deformation, strains and stresses within the section are all shown in diagrammatic form for the three stages and related to the load deflection response in Figures 4-6.
Stage 1 - Figure 4
For very low loads the steel and concrete behaves in an approximately linear way. The connection between the two carries very low shear stresses and it is unlikely that appreciable longitudinal slip will occur. The beam deforms so that the strain distribution at mid span is linear, as in Figure 4, and the resulting stress is also linear.
It can be seen from the strain diagram that, in this case, the slab must be deep as the neutral axis lies within the concrete. As a result some of the concrete is in tension. It has been assumed that this concrete cracks and therefore carries no tensile stress. If the slab was thin it is possible that the neutral axis would be in the steel and then the area of steel above the axis would be in compression.
This stage corresponds to the service load situation in the sagging moment region of most practical composite beams.
Stage 2 - Figure 5
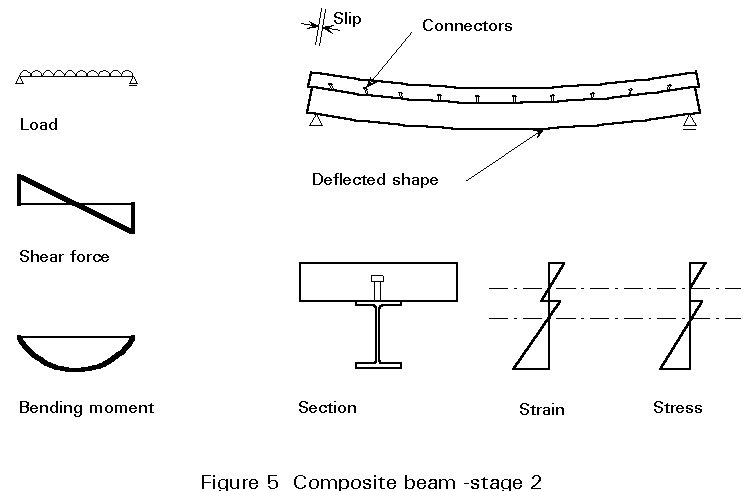
As the load increases the shear stress between the slab and steel section gives rise to deformation in the connection. This deformation is known as 'slip' and contributes to the overall deformation of the beam. Figure 5 shows the effect of slip on the strain and stress distribution. For many composite beams slip is very small and may be neglected (exceptions to this assumption will be covered later in this lecture and in Lecture 10.6.2).
This stage corresponds to the service load stage for that class of composite beams which has been designed as partially connected. This class of composite beam will be described more fully later in the lecture and in detail in Lecture 10.6.2.
Stage 3 - Figures 6 and 7
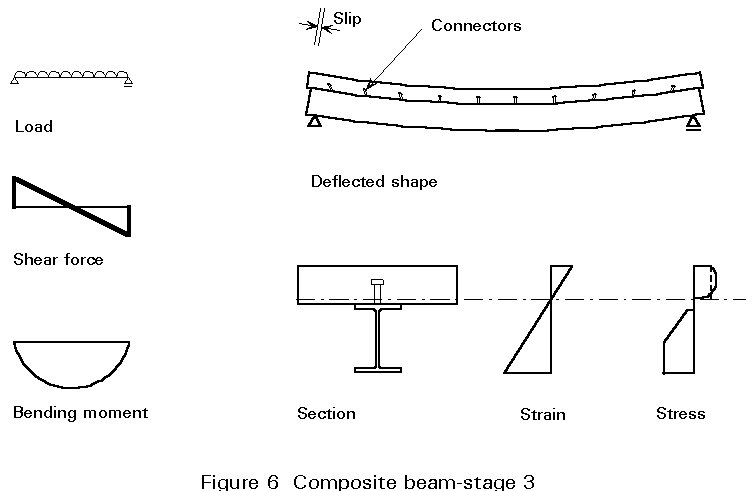
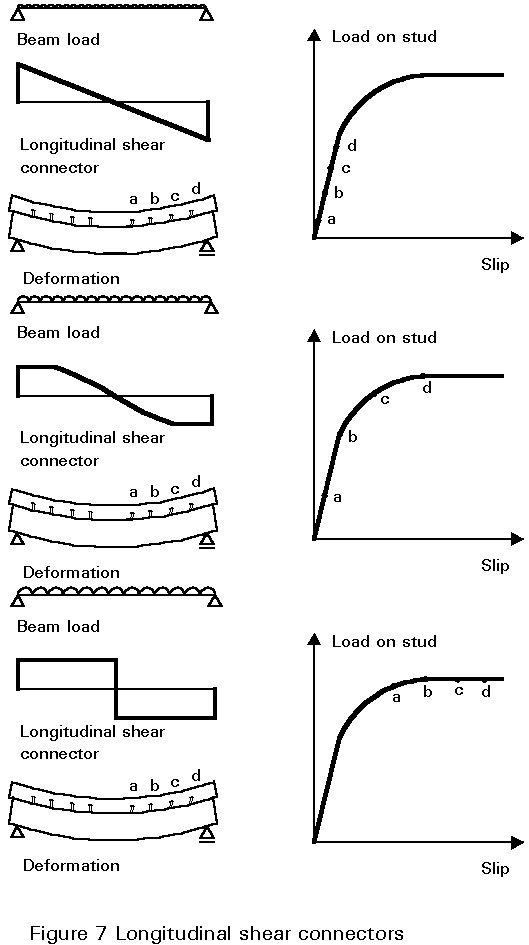
Eventually the load becomes sufficient to cause yield strains in one or more of the materials.
Stage 3a
In the case of yield occurring in the steel, plasticity develops and the stress block develops as shown in Figure 6. It is normally assumed that, for the ultimate limit state, the plastic stress block develops such that the whole steel section may eventually reach yield as shown by the dotted line in Figure 6.
Stage 3b
Concrete is not a plastic material. If strains develop such as to cause overstress it is potentially possible that explosive brittle failure of the slab would occur. This behaviour would be similar to the brittle failure expected in an over-reinforced concrete beam. The volume of concrete in most practical slabs means that it is unlikely that this situation could ever arise in practice.
With increase in stress within the concrete, induced by increasing strain, the stress block changes from the triangular shape shown in Figure 5 to the shape shown in Figure 6. For design this shape is difficult to represent in mathematical form and approximations are used. These approximations will be covered in more detail in Lecture 10.3. For composite beams the most common approximation is the rectangular stress block shown by the dashed line in Figure 6 and in more detail in Figure 2b.
Stage 3c
The remaining components of the composite beam that may fail before the steel yields or the concrete crushes are the connectors. As the load increases the shear strain, and therefore the longitudinal shear force between the concrete slab and steel section, increases in proportion. For a uniformly loaded, single span, composite beam which is assumed to deform in an elastic manner the longitudinal shear force per m length of the beam (T) between slab and steel section can be obtained from the expression:
T = V S/I
where S is the first moment of area.
Since the longitudinal shear force is directly proportional to the applied vertical shear force, the force on the end connectors is the greatest. For low loads the force acting on a connector produces elastic deformations. This the slip between the slab and the steel section will be greatest at the end of the beam. The longitudinal shear and deformation of a typical composite beam, at this stage of loading, are shown in Figure 7a.
If the load is increased the longitudinal shear force increases, and the load on the end stud may well cause plastic deformation. A typical load slip relationship for the connectors is shown in Figure 7. The ductility of the connectors means that the connectors are able to deform plastically whilst maintaining resistance to longitudinal shear force. Figure 7b shows the situation when the two end connectors are deforming plastically.
Increasing applied load will produce increasing longitudinal shear and connector deformation. In consequence, connectors nearer to the beam centreline also begin sequentially to deform plastically. Failure occurs once all of the connectors have reached their ultimate resistance as shown in Figure 7c. This sequence of shear load and connector straining is shown in an exaggerated manner in Figures 7a, b, and c.
This failure pattern is dependent upon the connectors being able to deform plastically. The end connector in Figure 5 must be able to deform to a considerable extent before the connector close to the beam centreline even reaches its ultimate capacity. This requirement for ductility will be discussed further in Lecture 10.6.1 where it will be shown to dictate beam span.
It can be seen that the failure of the composite beam is dictated by the resistance of its three main components. As the elastic interaction of these components is very complex it is normal to design these sections assuming the stress distribution shown in Figure 2b.
Composite beams designed to fail when the steel yields, the concrete just reaches a failing strain and all of the connectors deform plastically would appear to be the ideal situation. There are however several reasons why this situation rarely occurs. The reasons are investigated below.
It has been assumed so far that the loading on the beam is uniformly distributed and gives rise to a parabolic bending moment diagram. This is a common situation but it is also equally possible to find situations where concentrated loads act on beams.
In the case of uniform loading the maximum bending moment occurs at mid span. This section is then termed the critical section in bending. The stress block at the critical section is that described in Figure 6. It results in a longitudinal shear distribution to the shear connectors shown in Figure 7c. It can be seen that the longitudinal shear developed at the critical section must be resisted by the connectors between this point and the end of the beam. It can be deduced that, if the critical section is closer to the beam end, as would be the case for a single point load close to the support, the number of connectors between this point and the support needs to increase.
In practice the number of connectors between each load point on a beam subject to multiple point loads must be determined. This calculation often gives rise to variable spacing of connectors along the span length.
Point loads may also give rise to high vertical shear force. Although some of the vertical shear may be carried by the slab and beam flanges, it is common practice to ignore that and assume all the vertical shear is carried by the web of the steel section.
For continuous beams, discussed later in the lecture, there is a possibility of high shear and bending occurring together. In this case the moment resistance of the section is reduced. This aspect has been covered in detail in Lecture 7.8.2 and is also discussed in Lecture 10.4.2.
Concrete is subject to two phenomena which alter the strain and therefore the deflection of the composite beam.
During casting the wet concrete gradually hardens through the process of hydration. This chemical reaction releases heat causing moisture evaporation which in turn causes the material to shrink. As the slab is connected to the steel section through the shear connectors, the concrete shrinkage forces are transmitted into the steel section. These forces cause the composite beam to deflect. For small spans this deflection can be ignored, but for very large spans it may be significant and must be taken into account.
Under stress, concrete tends to relax, i.e., to deform plastically under load even when that load is not close to the ultimate. This phenomenon is known as creep and is of importance in composite beams. The creep deformation in the concrete gives rise to additional, time dependent, deflection which must be allowed for in the analysis of the beam at the service load stage.
The geometry of most composite beams is often predetermined by the slab size, as previously discussed, and by the capability of the steel section to carry the load of wet concrete during construction. This construction limitation gives rise to two composite beam types, the propped and the unpropped composite beam.
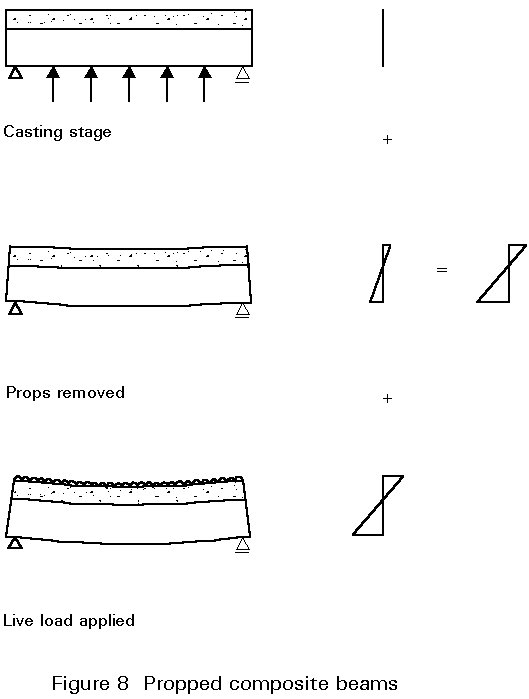
Consider first the case of the propped beam shown in Figure 8. During construction the steel section is supported on temporary props. It does not have to resist significant bending moment and is therefore unstressed and does not deflect. Once the concrete hardens the props are removed. Each of the component parts of the beam then takes load from the dead weight of the materials. However, at this stage, the beam is acting as a composite element and its stiffness and resistance are very much higher than that of the steel section alone. The deformation due to dead loads is, therefore, small. Any further live loading causes the beam to deflect. The total stresses present in the beam can be found by summing the stresses due to dead and live loads.
Consider now the unpropped beam shown in Figure 9. During construction the steel section is loaded with the dead weight of wet concrete. The steel section is stressed and deforms. The concrete and the connectors remain largely unstressed, apart from the shrinkage stresses developed within the hardened concrete. It can be seen, in Figure 9, that the wet concrete ponds, i.e. the top surface of the concrete remains level and the bottom surface deforms to the deflected shape of the steel section. The dead load due to the weight of wet concrete is a substantial proportion of the total load and the stresses developed in the section are often high.
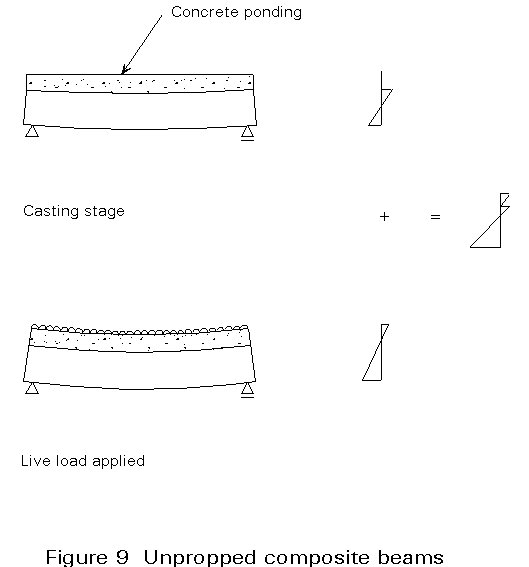
Additional live loads are carried by the composite section which has almost the same stiffness as that of the propped beam. The stresses present in the unpropped section can therefore be obtained by summing the wet concrete stresses and the composite stresses. This calculation leads to a different stress distribution in the section to that present in the propped composite beam. However the yield stresses developed in the steel and concrete are the same in both cases and both unpropped and propped composite beams carry the same ultimate load.
The steel section of an unpropped composite beam often needs to be substantial so that the weight of wet concrete can be carried. The section is, in fact, often substantially larger than would be required if the beam had been propped.
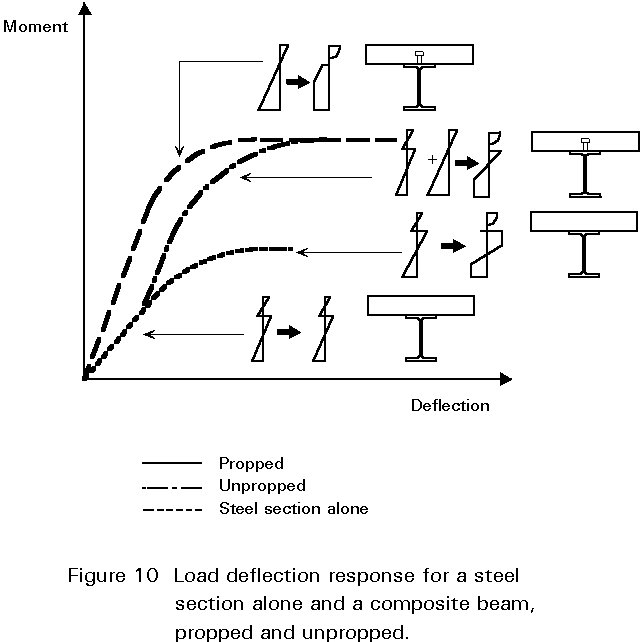
The load deflection response of a steel section alone and of a composite beam, both propped and unpropped, is shown in Figure 10. The strains present and stresses developed are shown in sequence with the section upon which they act. In the unpropped case the steel section alone takes the load of wet concrete and the strains due to this wet concrete load are added to the strains caused by the subsequently applied service loads. The resulting stresses are shown in the stress block. Whilst the overall deflection of the unpropped beam may be larger than the propped beam at the working load stage this is often not important as the deflection occurring during construction can be hidden by the finishes.
Despite the drawbacks discussed above, unpropped construction is often preferred for the following reasons:
In unpropped construction the size of the steel section is often determined by the weight of wet concrete, and the size of the slab is determined independently by its transverse span. If sufficient connectors are provided to transfer the maximum longitudinal force in the steel section or concrete slab, the resistance of the unpropped composite beam becomes very high. Indeed composite beams so formed are often capable of carrying several times the required live load. To avoid providing such excess resistance the partially connected composite member is used.
It has been assumed so far that the connection will carry all the shear force in the beam up to the time when the steel section has fully yielded. However, because the resistance of the unpropped beam is so high, it is often possible to reduce the number of connectors. This reduction results in a beam where the failure mode would be by connector failure prior to the steel having fully yielded or the concrete having reached its crushing strength.
Such beams require fewer connectors thereby reducing the overall construction cost. They are, however, less stiff since fewer connectors allow more slip to occur between the slab and steel section. Partial connection will be covered more fully in Lecture 10.6.2.
Although simply supported beam design is most common there may be situations where use of continuous beams is appropriate. These beams will be covered in detail in Lecture 10.4.1 and 10.4.2 and only a brief review will be presented here.
The mid span regions of continuous composite beams behave in the same way as the simple span composite beam. However the support regions display a considerably different behaviour. This behaviour is shown diagrammatically in Figure 11.
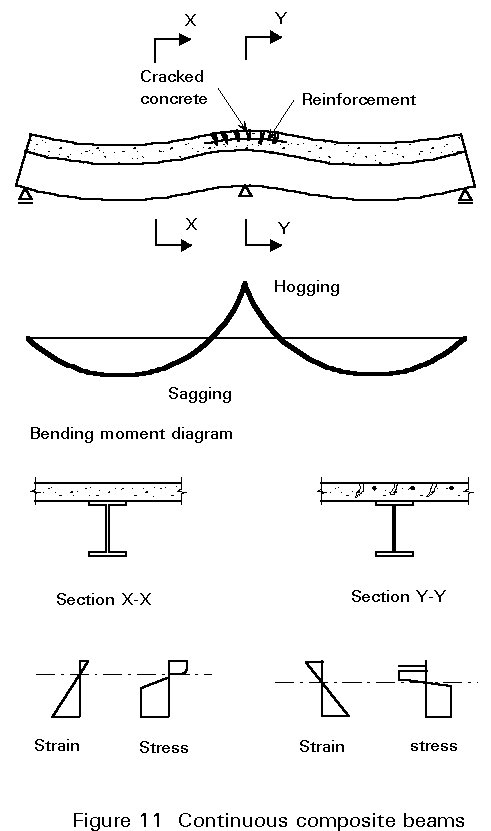
The concrete in the mid span region is generally in compression and the steel in tension. Over the support this distribution reverses as the moment is now hogging. The concrete cannot carry significant tensile strains and therefore cracks, leaving only the embedded reinforcement as effective in resisting moment.
The steel section at the support then has to carry compressive strains throughout a considerable proportion of its depth. Slender sections are prone to local buckling in this region and any intervening column section may need to be strengthened to absorb the compression across its web.
As well as local buckling it is possible that lateral-torsional buckling of the beam may occur in these regions.