
ESDEP WG 10
COMPOSITE CONSTRUCTION
To describe the behaviour of continuous composite beams; to explain the use of rigid-plastic analysis to determine internal moments and forces, and to derive plastic resistance moments.
Lecture 7.2: Cross-Section Classification
Lecture 7.3: Local Buckling
Lecture 10.2: The Behaviour of Beams
Lecture 10.3: Single Span Beams
Lecture 10.4.2: Continuous Beams II
Lectures 10.5: Design for Serviceability
Lectures 10.6: Shear Connection
The advantages of continuous beams are summarised and failure modes which result from continuity in composite beams are identified. Plastic methods may be used to determine internal moments and forces, provided that rotation capacity is sufficient and lateral-torsional buckling does not occur. The scope for plastic methods is related to classification of cross-sections in terms of limiting breadth/thickness ratios for structural steel elements in compression. Other measures needed to ensure adequate rotation capacity are also described. Simple values for effective width of the concrete flange are presented and expressions for the negative resistance moment of Class 1 and Class 2 sections are given. The application of rigid-plastic analysis to determine the distribution of bending moments is demonstrated.
Continuous beams offer the following advantages over simple construction:
These result in a smaller steel section being required to withstand specified loading.
In this lecture, members are assumed to be continuous over simple supports or to be rigidly connected to columns in braced frames. Additional cost will be incurred if special methods, such as more complicated jointing, have to be provided to achieve continuity. However, continuity of structural steel can be achieved economically by running a single length of section across two or more spans. The concrete is cast continuously over the supports and, to control shrinkage and other cracking, the concrete is reinforced. A typical cross-section of a composite beam, in the region of an internal support, is shown in Figure 1.

The disadvantages associated with continuous construction are:
After conceptual structural design has been done, which might possibly include initial sizing of members based on experience or rough calculations, the designer will wish to proceed to detailed calculations for the structure. The next stage is therefore determination of internal moments and forces in critical regions for the various loading cases and limit states. This is known as "global analysis" and procedures for this, at the ultimate limit state, are discussed here and in the following lecture.
Internal moments in continuous composite beams may be conveniently determined by elastic analysis or, subject to certain conditions, by rigid-plastic analysis. Whether plastic analysis is appropriate depends on the ductility of the reinforcement and on the susceptibility of the steel section to local buckling, as explained below. Elastic analysis is treated in the following lecture.
This is a well-established method of analysis for determining internal moments and forces in continuous steel structures. It is based on the assumption that plastic regions are concentrated at discrete points which may be represented by "plastic hinges". For the analysis to be valid, critical cross-sections must be capable of developing and sustaining their plastic resistance moment until, under increasing load, sufficient regions have fully-yielded for the plastic hinges to form a mechanism.
The mechanism arises as a result of redistribution of moment which is achieved by rotation of the already-yielded regions. To ensure that the resulting strains can be accommodated without a reduction in resistance below the plastic moment, limitations must be placed on the slenderness of the elements of the cross-sections which are in compression. For steel structures, sections which can form a plastic hinge with the rotation capacity required for plastic global analysis, are designated Class 1 cross-sections. The limitations on flange slenderness and web slenderness for such sections are given in design recommendations, such as Eurocode 3 [1], as discussed in Lectures 7.2 and 7.3. These limitations recognise that some loss of rotation capacity due to local buckling will be offset by beneficial effects such as strain-hardening and the finite length of plastic regions. However, because of the latter effect, it is necessary that cross-sections away from the theoretical locations are also in Class 1, or at least in Class 2. By definition, Class 2 cross-sections can develop the plastic resistance moment of the section although local buckling limits the rotation capacity and prevents full redistribution of moment at such sections.
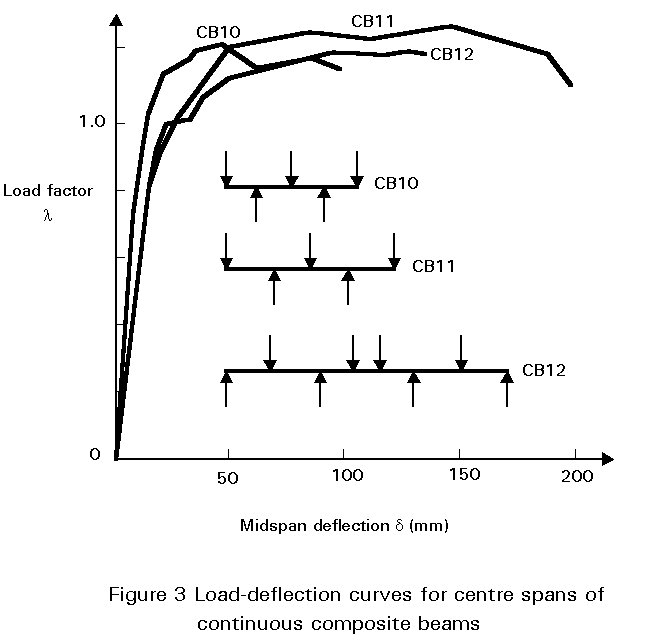
The flexural performance of continuous composite beams has been investigated by tests in which the secondary elements (shear connectors, transverse slab reinforcement) were conservatively designed in order to preclude forms of failure such as loss of interaction and longitudinal splitting of the slab. Initially, the behaviour is substantially linear (Figure 3), but as load increases reduction in flexural stiffness occurs.
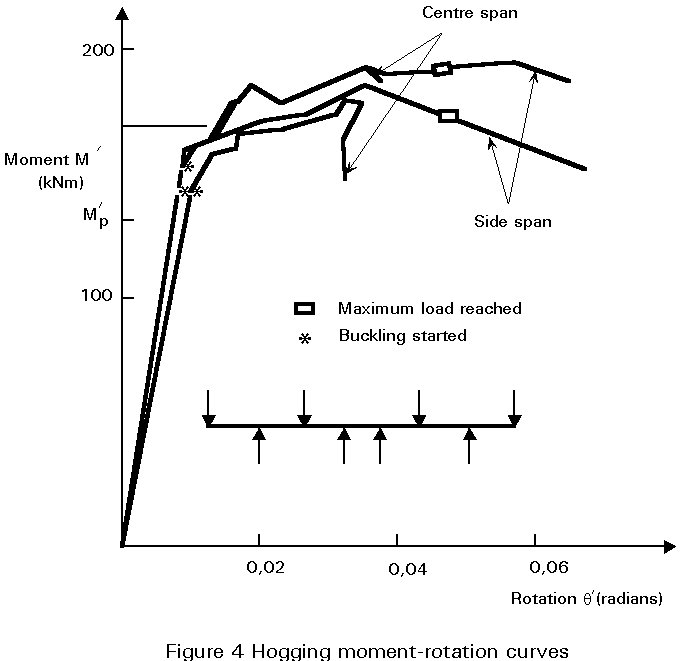
In hogging moment regions, fine cracks appear in the concrete at relatively low levels of load. As loading continues, cracking continues over an increasing length and yielding and later strain-hardening may occur in the reinforcement and in the lower (compression) part of the steel section. Redistribution of moment will occur to the mid-span regions. Provided that collapse of the beam is not triggered by crushing of the midspan concrete, by failure in shear, or by fracture of the reinforcement, the support section will develop flange buckles, eventually causing a loss of moment of resistance which initiates collapse (Figure 4).
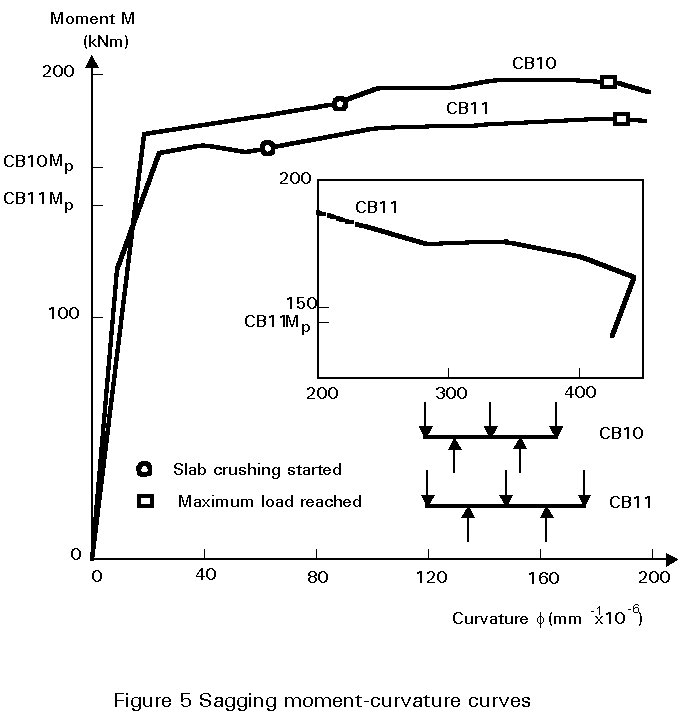
In mid-span sagging moment regions, yielding occurs in the lower part of the steel section and crushing occurs in the top of the concrete slab, causing redistribution of moment to the supports. Typical sagging moment-curvature curves are shown in Figure 5. The moment achieved can be significantly greater than the theoretical plastic resistance moment (Mpl) of the composite section, mainly on account of strain-hardening of the structural steel. It is evident from Figure 5, that deformation may continue without drop in moment for a considerable curvature. However, the rotation is small in composite beams having small slabs and/or weak concrete, large steel sections and/or high yield stress; in such beams crushing limits the rotation that will take place before reduction in moment occurs.
The nature of composite beams implies that a large amount of redistribution may be required before the collapse mechanism is complete.
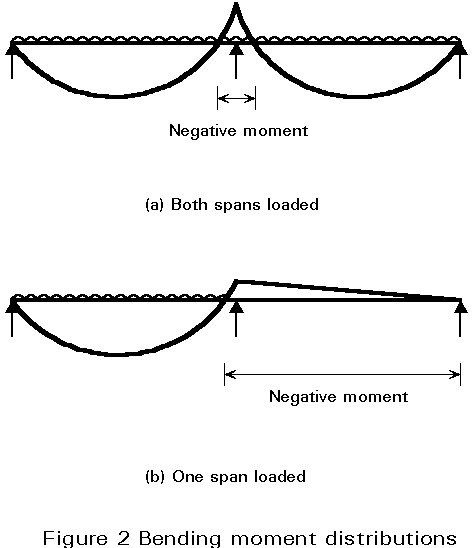
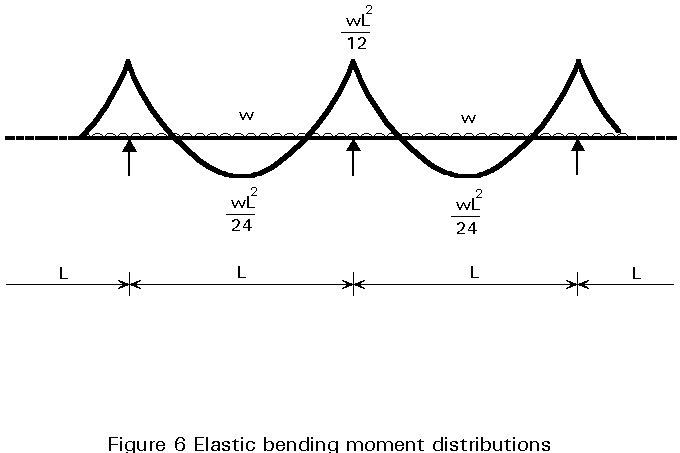
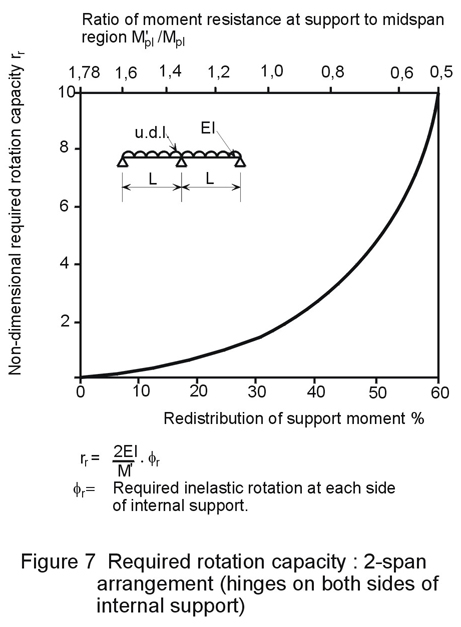
In the early stages of loading the beam behaves substantially elastically, with the bending moments at the supports and in the midspan region being unequal. For example, with a continuous beam of equal spans supporting uniform distributed loading (Figure 6), the bending moment at the supports is up to twice as large as that at midspan. However, the plastic resistance moment of midspan regions ranges from being larger than that at the support, sometimes by a factor as high as three, to being smaller (not usually the case). Consequently, a large amount of deformation can be required with redistribution being either from or to the support, the former being the usual case. Figure 7 shows as an example a two-span continuous beam subject to uniform distributed loading. The rotation required on each side of the support to complete a plastic hinge mechanism clearly increases as the resistance moment at the support (M¢pl) decreases relative to that at midspan (Mpl).
In continuous composite beams therefore, the rotation capacity required at a particular critical cross-section will depend on:
The eventual failure mode of a beam is strongly influenced by the strain-hardening and falling branch parts of the moment-rotation curves in the hogging and sagging regions, for which there is no simple method of prediction. Requirements for the satisfactory use of rigid-plastic analysis are therefore based on test results, supplemented by parametric studies undertaken by computer. The scope for the application of the method is therefore bounded by that of the parametric studies.
The requirements proposed in Eurocode 4 [2], Section 4.5.2.2, to achieve sufficient rotation capacity, permit the scope for rigid-plastic analysis to be given without reference to the strain-hardening properties of steel, which are not usually known by the designer. The requirements are:
It can be seen from the above requirements that, unlike steel structures, the definition of a Class 1 section in terms of limiting breadth/thickness ratios is not in itself sufficient to ensure always that enough rotation capacity will be available for plastic analysis in composite construction. Provided, however, that the requirements given above concerning relative lengths of spans and arrangement of loading are satisfied, the limits on breadth/thickness ratios for a Class 1 composite section can be taken as those for steel sections given in Eurocode 3 [1]. The limits for Class 1 and Class 2 sections, given in Tables 1(a) and (b) of this lecture, have been taken from Tables 4.1 and 4.2, respectively, of Eurocode 4 [2].
For Class 2 sections, web encasement may be assumed to contribute to resistance to local buckling, provided that it is reinforced and mechanically connected to the steel section.
The plastic resistance of a composite beam in sagging bending has been described in Lecture 10.2. The upper flange of the steel section may be in compression but is restrained laterally through its connection to the concrete slab.
The negative moment of resistance can be determined as described below. The lower flange of the steel section is now in compression. However, this flange is usually restrained laterally by connection to a supporting element, such as a column, which is itself prevented, at beam level, from moving out-of-plane.
It is assumed that the effect of co-existent vertical shear on the bending resistance can be neglected. When the shear force exceeds half the plastic shear resistance of the web of the steel section, allowance should be made for its effect on the resistance moment, as described in the previous lecture.
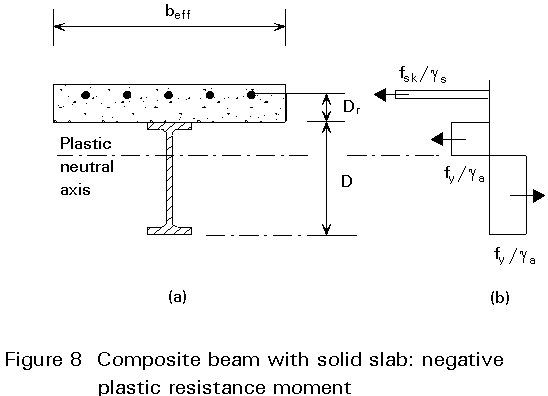
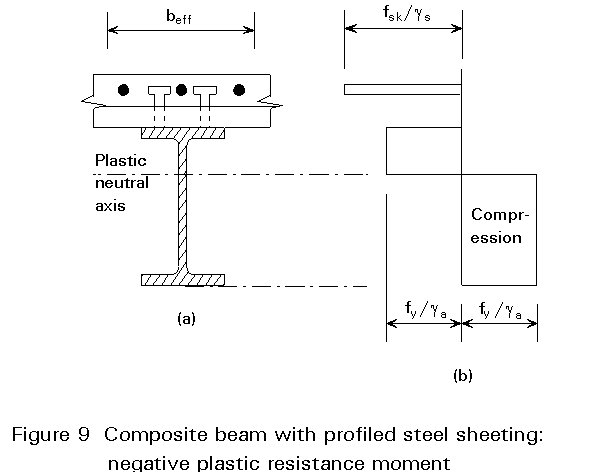
The cross-sections considered are shown in Figure 8(a) (for a solid slab) and Figure 9(a) (for a slab formed with profiled steel sheeting). As in positive moment regions, an effective width is used to make allowance for in-plane shear flexibility (shear lag) of the concrete flange.
The ratio of the effective width to the real flange width depends on many factors, including the type of loading, the support conditions, the cross-section considered and the ratio of beam spacing to span. In most design recommendations (particularly for buildings), however, very simple formulae are given for effective width, related to the span(s) of the beam and expressed in terms of a length lo between points of contraflexure; these should be taken simply as follows:
End span lo = 0,8L
Internal span lo = 0,7L
where L is the distance between supports for the span concerned, i.e. L1 or L2 in Figure 10, which has been taken from Figure 4.3 of Eurocode 4 [2]; this also gives a value appropriate for a span next to a cantilever, i.e. L3.

Research on shear lag in negative-moment regions has shown that when transverse reinforcement appropriate to the shear connector spacing is provided, the cracked slab is able to transfer shear to longitudinal reinforcement at a distance of several slab thicknesses on either side of the steel member. Over an internal support, Eurocode 4 gives:
lo = 0,25 (L1 + L2)
where L1 and L2 are the lengths of adjacent spans (Figure 10). Figure 10 also gives a value appropriate to the support region of a cantilever.
To determine the negative moment of resistance, generally all properly anchored reinforcing bars within the effective width are assumed to be stressed to their design yield strengths fsk/gs (Figure 8b). If the area of this reinforcement is Ar, then the tensile resistance of the reinforcement, Rr, within the effective width of the slab under negative moment is given by:
Rr = (fsk/gs)Ar
Due to the possibility of fracture caused by lack of ductility, nominal slab reinforcement (i.e. welded mesh or bars of less than 10mm diameter) should be neglected in calculating Rr. All bars included when calculating Rr should be of high ductility (Class H) as defined in Eurocode 2 [3].
At flexural failure, the whole of the concrete slab may be assumed to be cracked, whilst all the structural steel is at its design yield strength fy/ga in tension or compression. The plastic neutral axis may be in the top flange or in the web. For the latter case, the stresses are shown in Figure 8(b). The position of the neutral axis is determined by considering longitudinal equilibrium.
Let Rw be the axial resistance of the web over a depth d between the flanges. Then for a steel section with equal flanges, the plastic neutral axis will lie in the web if Rr<Rw, whilst if Rr>Rw, the neutral axis will lie in the steel flange. For each case an expression for the negative plastic resistance moment M¢pl, can be determined by considering the moment of each rectangular stress block about the neutral axis.
Case 1: Rr < Rw (plastic neutral axis lies in web)
M¢pl = Ma + Rr ![]()
where Ma is the plastic resistance moment of the steel section alone;
D is the overall depth of the steel section;
Dr is the distance from the top of the steel beam to the centroid of the reinforcement.
Case 2: Rr > Rw (plastic neutral axis lies in steel flange)
Assuming the thickness of the flange is small:
M¢pl = Rs ![]() + RrDr
+ RrDr
where Rs is the tensile resistance of the steel section. For a section of cross-sectional area Aa,
Rs = (fy/ga)Aa.
The cross-section shown in Figure 9 shows a slab formed with profiled steel sheeting. The sheeting component is usually neglected when determining the negative moment of resistance. For construction with profiled steel sheeting, it is common practice to provide only a light mesh reinforcement in the slab, which, as mentioned above, is neglected when calculating Rr. Thus if no further reinforcement is provided (additional to the sheeting and the mesh), the negative plastic resistance moment is given by M¢pl=Ma.
To design a suitable cross-section against flexure, it remains to determine the distribution of bending moments due to the applied load.
Let the ratio of the negative to the positive moments of resistance in a proposed section be y. Therefore:
y = M¢pl/Mpl
Consider the end span of a continuous composite beam, subject to a uniformly distributed design load of wf per unit length. The bending moment diagram at collapse is as shown in Figure 11.

It can be shown by analysis of the collapse mechanism that:
ß = ![]()
and the required value of Mpl is:
Mpl = ![]() wfß2L2
wfß2L2
For an internal span with equal support moments (Figure 12) it can similarly be shown that:
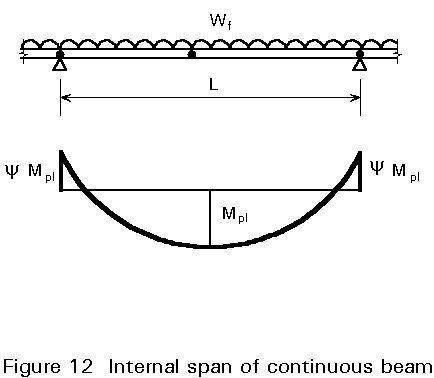
Mpl = wfL2/(8(1+y))
For other arrangements of loading and/or resistance moments, the required resistance may be determined from first principles.
[1] Eurocode 3: "Design of Steel Structures": ENV 1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.
[2] Eurocode 4: "Design of Composite Steel and Concrete Structures": ENV1994-1-1: Part 1.1: General rules and rules for buildings, CEN (in press).
[3] Eurocode 2: "Design of Concrete Structures": ENV 1992-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.
The references given in Lecture 10.1 are also relevant.