Previous | Next | Contents

Lecture 7.10.2: Beam Columns II

OBJECTIVE/SCOPE

To extend the introductory coverage of beam columns given in Lecture 7.10.1 to cover the full three-dimensional case.

PREREQUISITES

Simple bending and torsion theory

Lecture 7.2: Cross-Section Classification

Lectures 7.5: Columns

Lectures 7.8: Restrained Beams

Lectures 7.9: Unrestrained Beams

Lecture 7.10.1: Beam columns I

RELATED LECTURES

Lecture 7.11: Frames

RELATED WORKED EXAMPLES

Worked Example 7.10: Beam Columns

SUMMARY

This lecture expands on the treatment of beam-columns given in Lecture 7.10.1 to include the cases of out-of-plane buckling and biaxial bending. The basis for the Eurocode 3 interaction formulae is discussed and related to physical behaviour [1].

1. INTRODUCTION

Lecture 7.10.1 introduced all the main aspects of beam-column behaviour and design within the context of the uniaxial in-plane case. More general forms of response are, however, possible. This lecture broadens the coverage to include all of the main cases.

2. FORMS OF BEHAVIOUR

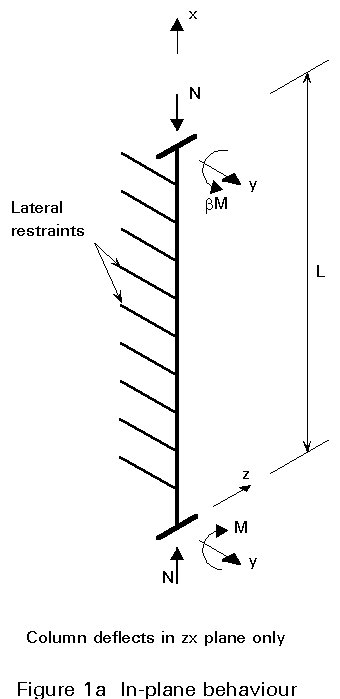
Three separate forms of beam-column behaviour are illustrated in Figure 1.

If the member is bent about its weaker principal axis, or is prevented from deflecting laterally when bent about its stronger principal axis as shown in Figure 1a, then its response will be confined to the plane of bending. This case has been covered in Lecture 7.10.1.

When a laterally unbraced beam-column of open cross-section is bent about its stronger principal axis as shown in Figure 1b, then it may buckle prematurely out of the plane of loading by deflecting laterally and twisting. Such behaviour is conceptually and mathematically very similar to the lateral-torsional buckling of beams described in Lectures 7.9.1 and 7.9.2.

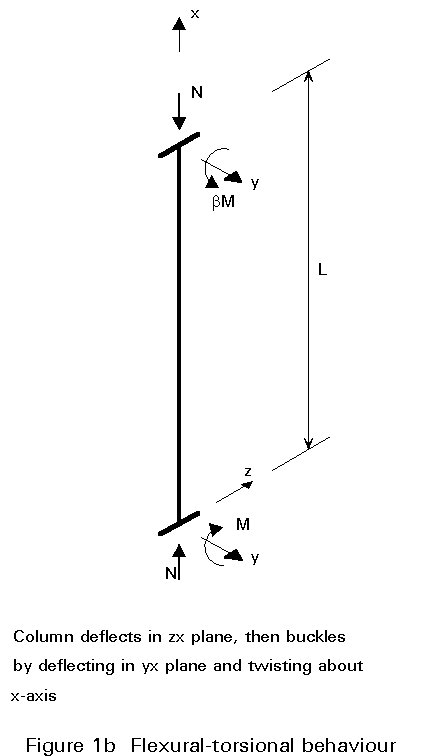
The most general situation is illustrated in Figure 1c. When bending is applied about both principal axes the member's response will be 3-dimensional in nature, involving biaxial bending and twisting.

In Figure 1 the nature of the interaction in each case is listed in the caption. Clearly the behaviour shown as Figure 1c is the most general, with that of Figures 1a and 1b being simpler and more limited cases. For a full treatment of the in-plane case of Figure 1a refer back to Lecture 7.10.1.

3. FLEXURAL-TORSIONAL BUCKLING

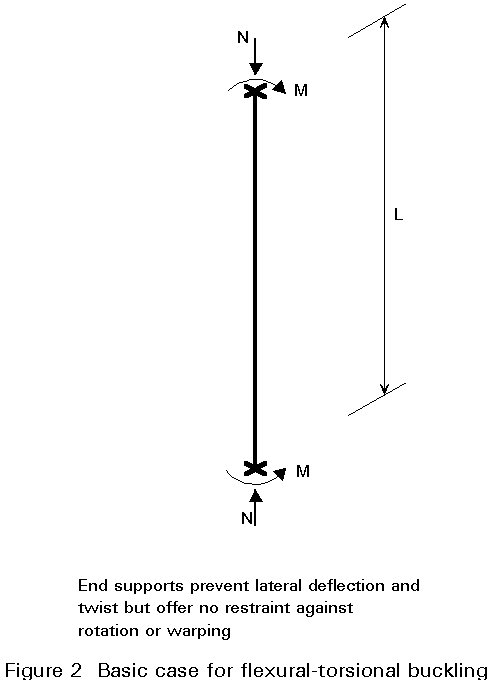
When a laterally unrestrained I-section beam-column is bent about its major axis, it may buckle by deflecting laterally and twisting at a load which is significantly less than the maximum load predicted by an in-plane analysis. Assuming elastic behaviour and the arrangement of applied loading and support conditions given in Figure 2, the critical combinations of N and M may be obtained from the solution of:

= (1)

in which i_o = [(I_y + I_z)/A]^1/2 is the polar radius of gyration

N_z = p² EI_z/L² is the minor axis critical load

N_o = (GJ/i_o²) (1 + p² EI_w/GI_tL²) is the torsional buckling load

Equation (1) reduces to the buckling of a beam when N ® 0 and to the buckling of a column in either flexure (N_z) or torsion (N_o) as M ® 0. In the first case the critical value of M will be given by:

M_cr = 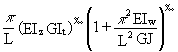(2)

in which EI_z is the minor axis flexural rigidity

GI_t is the torsional rigidity

EI_w is the warping rigidity

In deriving Equation (1) no allowance was made for the amplification of the in-plane moments M by the axial load acting through the in-plane deflections. As explained in Lecture 7.10.1 this may be approximated as M/(1-N/N_y). Equation (1) can, therefore, be modified to:

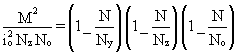(3)

Noting the relative magnitudes of N_y, N_z and N_o and re-arranging gives the following approximation:

N/N_z + {1/(1-N/N_y)}{M/i(N_zN_o)^1/2} = 1 (4)

or

N/ N_z + {1/(1-N/ N_y)}M/M_cr = 1 (5)

4. DESIGN

For design purposes it is necessary to make suitable allowances for effects such as initial lack of straightness, partial yielding, residual stresses, etc., as has been fully discussed in earlier lectures in the context of columns and beams. Thus some modification to Equation (5) is necessary to make it suitable for design. In particular, the end points (corresponding to the cases of M = 0 and N = 0) must conform to the established procedures for columns (Lectures 7.5.1 and 7.5.2) and beams (Lectures 7.9.1 and 7.9.2).

Eurocode 3 [1] uses the interaction equation:

£ 1 (6)

In which k_LT is a coefficient whose value depends upon:

• the level of axial load as measured by the ratio N_sd / c_z A f_y.
• the member slenderness _z.
• the pattern of primary moments.

and c_LT is the reduction factor for lateral-torsional beam buckling.

For the most severe combination k_LT adopts the value unity, corresponding to a linear combination of the compressive and bending terms. This reflects the reduced scope for amplification effects in this case, since the value of N_sd cannot exceed c_z A f_y, which will, in turn, be significantly less than the elastic critical load for in-plane bucking N_y.

It is, of course, also necessary to ensure against the possibility of in-plane failure by excessive deflection in the plane of the web at a lower load than that given by Equation (6). This might occur, for example, in situations where different bracing and/or support conditions are provided in the xy and xz planes as illustrated in Figure 3. 

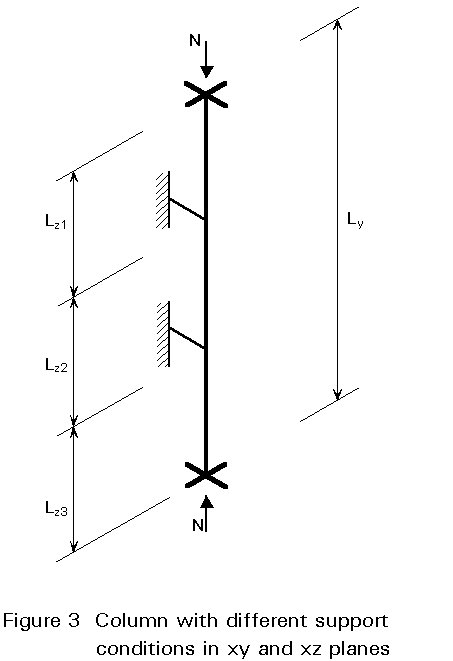
Such cases should be treated by checking, in addition to Equation (6), an in-plane equation of the form:

£ 1 (7)

in which c_min depends on the in-plane conditions. Usually, however, Equation (6) will govern.

5. BIAXIAL BENDING

Analysis for the full 3-dimensional case, even for the simple elastic version, is extremely complex and closed-form solutions are not available. Rather than starting analytically it is more convenient to approach the question of a suitable design approach from considerations of behaviour and the use of the methods already derived for the simpler cases of Figures 1a and 1b.

Figure 4 presents a diagrammatic version of the design requirement. The N-M_z and N-M_y axes correspond to the two uniaxial cases already examined. Interaction between the two moments M_z and M_y corresponds to the horizontal plane. When all three load components N, M_z and M_y are present the resulting interaction plots somewhere in the 3-dimensional space represented by the diagram. Any point falling within the boundary corresponds to a safe combination of loads.

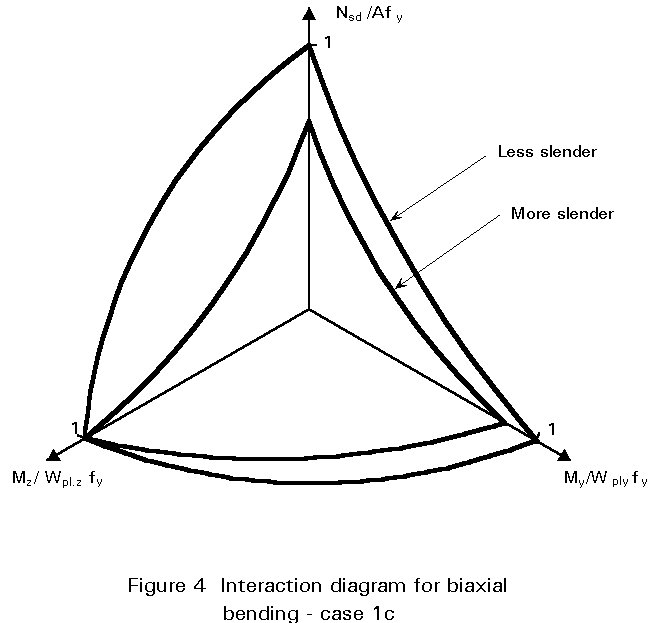
Assuming proportional loading any load combination may be regarded as a straight line starting at the origin, the orientation of which depends upon the relative sizes of the three load components. Increasing the loads extends this line from the origin until it just reaches and then exceeds the boundary. Non-proportional loading would correspond to a series of lines.

In each case the axes have been taken as the ratio of the applied component to the member's resistance under the load component alone, e.g. N_sd / c_min Af_y in the case of the compressive loading. Thus Figure 4 actually represents the situation for one particular example with particular values of cross-sectional properties, slenderness and load arrangement. Changing some or all of these will alter the shape of the interaction surface shown, but not the general principle involved.

6. DESIGN FOR BIAXIAL BENDING AND COMPRESSION

For design purposes, it is necessary to have a convenient representation of the situation described in Section 5 by using an interaction equation containing the three load components N, M_z and M_y. Parts of this equation, corresponding to the two 2-dimensional cases represented by the N, M_z and N, M_y planes, have already been discussed. The full equation must clearly reduce to these in the absence of the third load component.

Eurocode 3 [1] uses the pair of formulae:

£ 1 (8)

£ 1 (9)

Two checks are necessary because, under the action of compression plus major axis moment on an I-section with different support conditions in the zx and yx planes, it is not known whether the in-plane or out-of-plane interaction will be the more critical; that is to say whether, in the absence of M_z, failure would occur as shown in Figure 1a or Figure 1b. For the same conditions in both planes and _z > _y, c_min will correspond to c_z and Equation (9) will govern since c_LT, the reduction factor for lateral-torsional buckling under pure bending, will be less than or (if _LT is small) equal to unity.

For cross-sections not susceptible to lateral-torsional buckling, e.g. tubes, only Equation (8) is required since c_LT = 1.

7. TREATMENT OF OTHER THAN CLASS 1 OR 2 SECTIONS

The design formulae given as Equations (6) - (9) relate specifically to the case of Class 1 or 2 sections, i.e. those for which the proportions of the plate elements meet the limitations necessary to ensure the development of full cross-sectional plasticity, as explained in Lecture 7.2. When using either Class 3 or Class 4 sections some modifications are necessary.

For Class 3 cross-sections the quantities W_pl.y and W_pl.z should be replaced by the equivalent elastic quantities W_el.y and W_el.z.

When Class 4 sections are being employed the section properties A and W must relate to the effective cross-section; the shift of the neutral axis of the effective cross-section from its original position due to loss of effectiveness of some parts of the cross-section must also be allowed for. Thus Equations (8) and (9) become:

 £ 1 (10)

 £ 1 (11)

in which A_eff, W_eff.y and W_eff.z are the effective properties in the presence of only uniform compression or moment about the y and z axes respectively and e_N is the shift of the neutral axis when the cross-section is subject to uniform compression.

An important point to note from the definition of A_eff and W_eff above is that the calculation of cross-sectional properties, and thus also cross-sectional classification, should be undertaken on a separate basis for each of the three load components N, M_y and M_z. This does, of course, mean that the same member may be classified as (say) Class 1 for major-axis bending, Class 2 for minor-axis bending and Class 3 for compression. In such cases the safe design approach is to conduct all beam-column checks using the procedures for the least favourable class.

8. DETERMINATION OF k-FACTORS

The value of k_LT for use in Equation (6) is actually given by:

   (but k_LT £ 1) (12)

in which m_LT = 0,15_z b_M.LT - 0,15 (but m_LT £ 0,90) (13)

and b_M.LT is the equivalent uniform moment factor for lateral-torsional buckling determined from Table 2.

In Equations (7) - (11) the values of k_y and k_z should be obtained from:

k =       but k £ 1,15 (14)

m =  (2b_M- 4) + (W_pl - W_el)/W_el       but m £ 0,9 (15)

in which m, c, , b_M, W_pl and W_el all relate to the axis under consideration, i.e. y or z, and b_M is determined from Table 2.

For Class 3 or 4 cross-sections the second term in Equation (15) should be omitted.

9. CROSS-SECTION CHECKS

If allowance has been made when determining the k-factors (through the use of b_M) for the less severe effect of patterns of moment other than uniform single curvature bending, it is necessary further to check that the cross-section is everywhere capable of locally resisting the combination of compression and primary moment(s) present at any point. This location will usually be one or other of the ends as explained in Lecture 7.10.1.

Expressions for checking several types of cross-section under compression plus uniaxial bending were given in Lecture 7.10.1. For biaxial bending Eurocode 3 [1] uses:

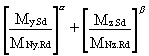£ 1 (16)

in which the values of a and b depend upon the type of cross-section as indicated in Table 1.

A simpler but conservative alternative is:

    £ 1 (17)

10. CONCLUDING SUMMARY

• Depending on the form of the applied loading, 3 types of beam-column problem may be identified.
• The biaxial bending case is the most general and includes the 2 others as simpler and more restricted component cases.
• Interaction equations are used for design purposes.
• These make use (as end points) of the design procedures for beams (N = 0) and columns (M = 0).
• The class of cross-section will affect some of the values used in the interaction equations.

11. REFERENCES

[1] Eurocode 3: "Design of Steel Structures": ENV 1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.

12. ADDITIONAL READING

1. Chen, W. F. and Atsuta, T., "Theory of Beam-Columns" Vol. 2, McGraw-Hill, 1977.

Comprehensive treatment of the beam-column problem for the cases of flexural-torsional bucking and biaxial bending.

2. Trahair, N. S. and Bradford, M. A., "Behaviour and Design of Steel Structures", 2nd edition, Chapman and Hall, 1988.

Chapter 7 refers to beam-columns, including a comparison of the subject's treatment in three design codes (not including Eurocode 3).

3. Ballio, G. and Mazzolani, F. M., "Theory and Design of Steel Structures", Chapman and Hall, 1983.

Gives basis of original European approaches to the use of interaction formulae, including derivations.

4. Galambos, T. V., "Guide to Stability Design Criteria for Metal Structures", 4th edition, Wiley Interscience.

Chapter 8 presents a comprehensive review of theoretical, experimental and design-oriented contributions to the topic of beam-column behaviour.

5. Dowling, P. J., Owens, G. W. and Knowles, P., "Structural Steel Design", Butterworths, 1988.

Chapter 24 deals with beam-column behaviour and design, including explanations of the physical significance of the concepts of interaction and slenderness.

6. Nethercot, D. A., "Limit State Design of Structural Steelwork", 2nd edition, Chapman and Hall, 1991.

Chapter 6 deals with beam-column behaviour and design.