Previous | Next | Contents

Lecture 7.8.1: Restrained Beams I

OBJECTIVE/SCOPE

To derive and discuss the procedures used to design restrained compact beams for bending, shear and deflection, according to the principles of Eurocode 3 [1].

PREREQUISITES

Elastic theory for uniaxial bending

Simple torsion theory

Lecture 7.2: Cross-Section Classification

RELATED LECTURES

Lecture 7.8.2: Restrained Beams II

Lectures 7.9: Unrestrained Beams

RELATED WORKED EXAMPLES

Worked Example 7.8: Laterally Restrained Beams

SUMMARY

This lecture is restricted to beams whose design may be based on simple strength of materials considerations. Behaviour in simple bending is discussed, leading to the concept of section modulus as the basis for strength design. Subsidiary considerations of shear strength, resistance to local loads and adequate stiffness against deflection are also mentioned. Behaviour under complex loading, producing bending about both principal axes, or combined bending and torsion is introduced.

ADDITIONAL NOTATION

A area

A_v shear area

d depth of section

F applied load

f_d limiting stress in material

f_y material yield strength

f_yd material design strength

I second moment of area

M moment

M_pl plastic moment

t thickness

t_f thickness of flange

t_w thickness of web

V_s shear due to applied load

W elastic section modulus

W_max maximum value of W

W_min minimum value of W

W_pl plastic section modulus

a,b coefficients, see Equation (7)

s normal stress

1. INTRODUCTION

Probably the most basic structural component is the beam, spanning between two supports, and transmitting loads principally by bending action. Steel beams, which may be drawn from a wide variety of structural types and shapes, can often be designed using little more than the simple theory of bending. However, situations will arise in which the beam's response to its loading will be more complex, with the result that other forms of behaviour must also be considered. The main purpose of this lecture is to concentrate on the design of that class of steel beam for which strength of materials forms the basis of the design approach. These are termed "restrained compact beams"; in order to come within this category the beam must not be susceptible to either local instability (see Lecture 7.2 for Class 4 beams) or lateral-torsional instability (see Lecture 7.9.1 and 7.9.2 for unrestrained beams). A further limitation is that the beams are assumed to be statically determinate or, if statically indeterminate, that the distribution of internal bending moments has been obtained on a simple linear elastic basis.

The first requirement will be met if the width of the individual plate elements of the cross-section are limited, relative to their thickness. Sections for which the ratios of flange width/flange thickness, web depth/web thickness etc, have been limited, so that their full plastic moment capacity may be achieved, correspond to either Class 1 or Class 2 according to Eurocode 3 [1]. The majority of hot rolled sections, e.g. UB's and IPE's, meet these requirements. However, care is necessary when using fabricated sections and suitable rules are provided in codes of practice. This lecture assumes that the beam cross-section will at worst correspond to Class 2 or Class 3 and that, if it meets the Class 1 limits, then the global analysis of the structure will be conducted using plastic methods.

Lateral-torsional instability will not occur if any of the following conditions apply:

• the section is bent about its minor axis.
• full lateral restraint is provided, e.g. by positive attachment of the top flange of a simply supported beam to a concrete slab.
• closely spaced, discrete bracing is provided so that the weak axis slenderness (L/i_z) of the beams is low.
• adequate torsional restraint of the compression flange is provided, e.g. by profiled sheeting.
• the section has high torsional and lateral bending stiffness; for example, rectangular box sections bent about their major axis are unlikely to fail in this way.

For the special case of continuous beams supporting a roof or floor, care must be taken to ensure adequate stability of those regions in which the bottom flange is in compression, e.g.the support region under gravity loading, the mid-span region under wind uplift, etc... For the purpose of this lecture, beams within any of these categories will be classed as "restrained".

2. BEAM TYPES

Several factors, some of them tending to conflict with one another, influence the designer's choice of beam type for a given application. Clearly the beam must possess adequate strength, but it should also not deflect too much. It must be capable of being connected to adjacent parts of the structure; this will often involve the use of site connections which should be simple and quick to erect, with minimum requirements for skilled labour or special equipment. Particular features, such as the passage of services beneath the floor of a building, may dictate the use of a section with openings in the web, whilst architectural requirements may require the profile to be varied, to improve the line. Table 1, summarising the main types of steel beam, indicates the range of spans for which each is most appropriate and gives some idea of any special features.

3. DESIGN OF BEAMS FOR SIMPLE BENDING

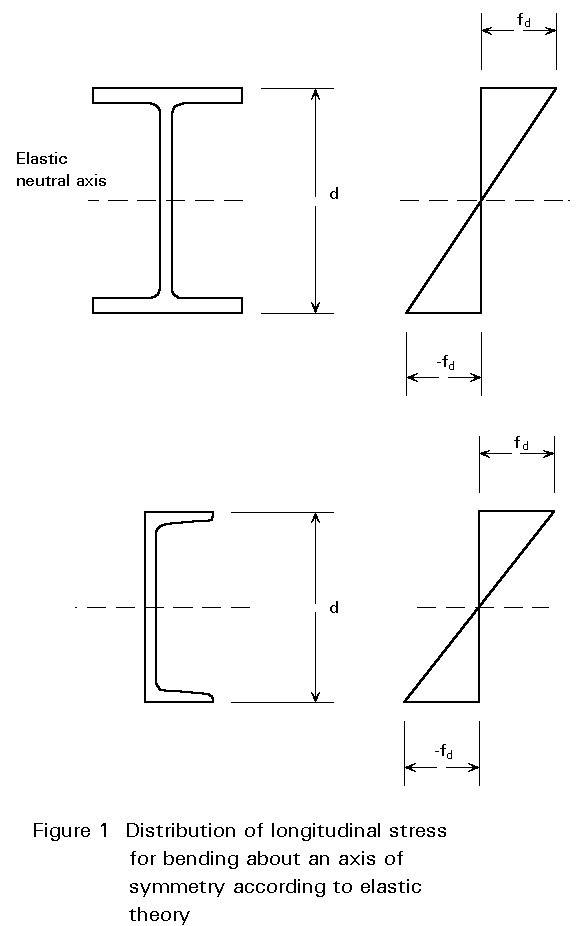
For a doubly-symmetrical section or a singly-symmetrical section bent about the axis of symmetry, the basic theory of bending, assuming elastic behaviour, gives the distribution of bending stress shown in Figure 1. 

Since the maximum stress s_max is given by:

s_max = (1)

where M is the moment at cross-section under consideration.

d is the overall depth of section.

I is the second moment of area about the neutral axis (line of zero strain).

it follows that limiting this to a fraction of the material yield stress gives a design condition of the form:

W ³ M/f_d (2)

where W =

f_d is the limiting normal bending stress.

When M is taken as the moment produced by the working loads, this approach to design is termed 'elastic' or 'permissible stress' design and is the method traditionally used in many existing codes of practice. In more modern Limit States codes f_d is taken as the material strength f_y possibly divided by a suitable material factor g_M and M is taken as the moment due to the factored loads i.e. the working loads suitably increased so as to provide a margin of safety in the design. Equation (2), in this case, represents the condition of first yield. Values of W for the standard range of sections are available in tables of section properties.

Selection of a suitable beam therefore comes down to:

1. determination of the maximum moment in the beam,
2. extraction of the appropriate value of f_d from a suitable code,
3. selection of a section with an adequate value of W subject to considerations of minimum weight, depth of section, rationalisation of sizes throughout the structure, etc...

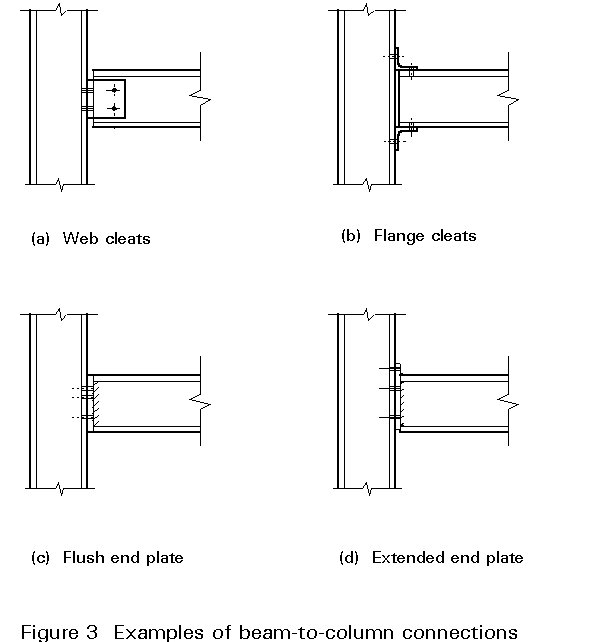
Clearly, sections for which the majority of the material is located as far away as possible from the neutral axis will tend to be the most efficient in elastic bending. Figure 2 gives some quantitative idea of this for some of the more common structural shapes. I-sections are most often chosen for beams because of their structural efficiency; being open sections they can also be connected to adjacent parts of the structure without undue difficulty. Figure 3 gives some typical examples of beam-to-column connections.

Utilisation of the plastic part of the stress-strain curve for steel enables moments in excess of those which just cause yield to be carried. At full plasticity the distribution of bending stress in a doubly-symmetrical section will be as illustrated in Figure 4, with half the section yielding in compression and half in tension. 

The corresponding moment is termed the fully plastic moment M_pl. It may be calculated by taking moments of the stress diagram about the neutral axis to give:

M_pl = f_y W_pl (3)

where f_y is the material yield stress (assumed identical in tension and compression).

W_pl is the plastic section modulus.

Basing design on Equation (3) means that the full strength of the cross-section in bending is now being used, with the design condition being given by:

W_pl ³ M/f_yd (4)

where M is the moment at cross-section under consideration.

f_yd is the design strength (material yield strength divided by a suitable material factor).

When M is due to the factored loads Equation (4) represents the design condition of ultimate bending strength used in Eurocode 3 for beams whose cross-sections meet at least the Class 2 limits [1]. It is usual in codes such as Eurocode 3 for the value of f_yd to be taken as the material yield strength, reduced slightly so as to cover possible variations from the expected value.

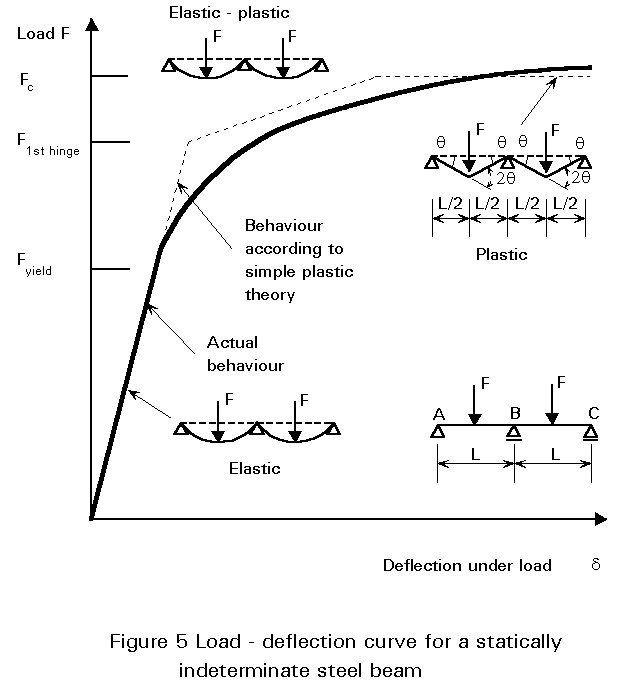
For continuous (statically indeterminate) structures, attainment of M_pl at the point of maximum moment will not normally imply collapse. Providing nothing triggers unloading at this point, e.g. local buckling does not occur, then the local rotational stiffness will virtually disappear, i.e. the cross-section will behave as if it were a hinge, and the pattern of moments within the structure will alter from the original elastic distribution as successive plastic hinges form. This redistribution of moments will enable the structure to withstand loads beyond that load which produces the first plastic hinge, until eventually collapse will occur when sufficient hinges have formed to convert the structure into a mechanism, as shown in Figure 5. Utilisation of this property of redistribution is termed "plastic design". It can only be used for continuous structures and then only when certain restrictions on cross-sectional geometry, member slenderness, etc.., are observed. The topic is covered in detail in Lecture 7.8.2 in the context of beams and in Lecture 7.11 in the context of frames.

4. DESIGN OF BEAMS FOR SHEAR

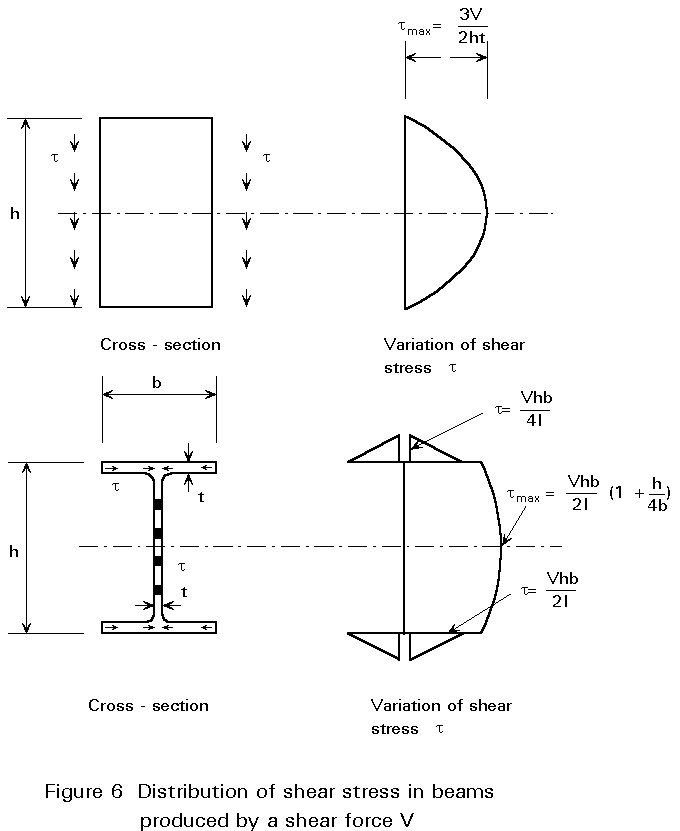
Although bending will govern the design of most steel beams, situations will arise, e.g. short beams carrying heavy concentrated loads, in which shear forces are sufficiently high for them to be the controlling factor.

Figure 6 illustrates the pattern of shear stress found in a rectangular section and in an I-section assuming elastic behaviour. In both cases shear stress varies parabolically with depth, with the maximum value occurring at the neutral axis. However, for the I-section, the difference between maximum and minimum values for the web, which carries virtually the whole of the vertical shear force, is sufficiently small for design to be simplified by working with the average shear stress, i.e. total shear force/web area. Since the shear yield stress of steel is approximately 1/Ö3 of its tensile yield stress, a suitable value for "permissible" shear stress when using elastic design is 1/Ö3 of the permissible tensile stress.

The ultimate shear resistance (based on plastic principles) used in Eurocode 3 [1] is f_yd/Ö3; this is used in conjunction with a shear area A_v, examples of which are:

rolled I-section, load parallel to web A_v = A-2bt_f + (t_w+2r)t_f

plates and solid bars A_v = A

circular hollow sections A_v = 2A/p

In cases where high shear and high moment coexist, e.g. the internal support of a continuous beam, it may sometimes be necessary to allow for interaction effects. However, since the full shear capacity may be developed in the presence of quite large moments and vice versa (Eurocode 3 only requires reductions in moment resistance when the applied shear exceeds 50% of the ultimate shear resistance [1]) this will not often be required.

5. DEFLECTIONS

Excessive deflections, whilst not normally leading to a structural failure, may, nonetheless, impair the serviceability of the structure.

Deflection might, for example, cause:

• cracking of plaster ceilings.
• misalignment of crane rails.
• difficulty in opening large doors.

Since these affect the performance of the structure in its working conditions, it is usual to conduct this type of check at service load levels. Eurocode 3 suggests a limit of span/300 for the maximum deflection of beams supporting floors under service live load [1]. Such limits should, however, be regarded as advisory only, and smaller or larger values can be more appropriate in any given situation. Wherever possible, specialist advice should be sought; crane manufacturers, for example, should be able to give detailed guidelines regarding permissable deflection for gantry beams.

6. BENDING OF UNSYMMETRICAL SECTIONS

For sections with a single axis of symmetry bent about the perpendicular axis, the elastic distribution of bending stresses will be as shown in Figure 7. Due to its lack of symmetry about the neutral axis, the stress on the top and bottom flanges will not be equal; for example, the stress on the smaller flange, in the case of an unequal flanged I-beam, will exceed that on the bigger. Therefore, in elastic design, it is necessary to use the smaller of the two elastic section moduli W_min.

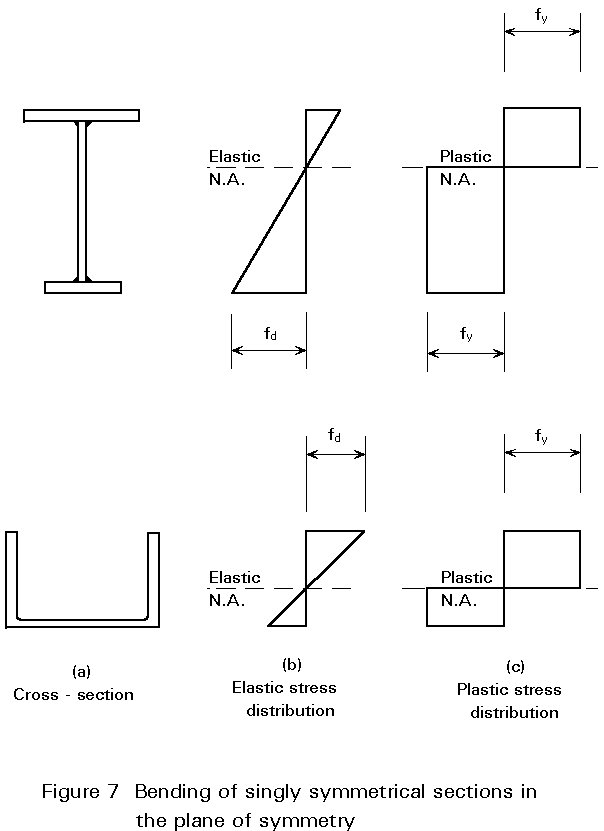
At full plasticity, the line of zero stress must be positioned so that it divides the area of the section into two equal parts, as shown in Figure 7c. Since the plastic section modulus W_pl is defined from Equation (3) as the ratio of M_pl/f_y, there will be a single value for both faces of the section. Thus, when using ultimate moment resistance, the design condition will remain as Equation (4).

7. BIAXIAL BENDING

Doubly or singly-symmetrical sections subject to bending moments M_y, M_z about both principal axes may be treated as the sum of two uniaxial problems. Thus, in elastic design, it is necessary to satisfy the linear interaction equation:

(6)

in which W_y and W_z are the elastic section moduli of the cross-section with respect to the axes y and z and

f_d is the limiting normal bending stress.

This is based on the idea of limiting the maximum combined stress in the section to the design value. Care is necessary when dealing with sections such as angles for which the principal axes are not rectangular.

When using the plastic strength of the cross-section, analysis (which entails the location of the plastic neutral axis) shows that the shape of the interaction between moments will depend upon the geometry of the cross-section. Safe approximations to these interaction diagrams have therefore been provided in Eurocode 3 [1]. These adopt the form:

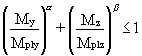(7)

in which M_ply and M_plz are moment capacities about the y and z axis respectively and the values of a and b depend on the particular section under consideration; safe values are a = b = 1,0.

8. BENDING AND TORSION

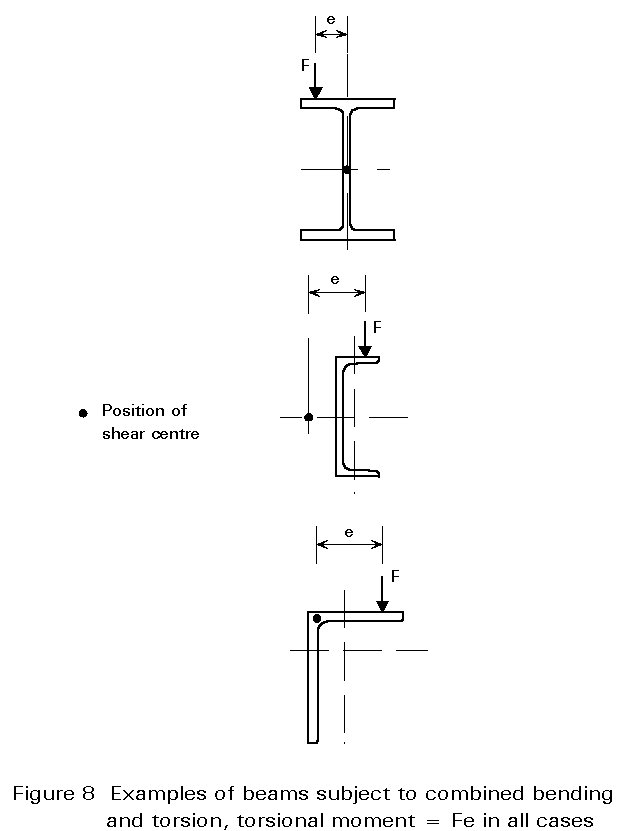
Loads which do not act through the shear centre of the section (see Figure 8) will also cause twisting (the shear centre coincides with the centroid for doubly-symmetrical sections, and lies on the axis of symmetry for singly-symmetrical sections.) This will induce shear stresses due to torsion and, in the case of open sections, may also produce significant additional longitudinal stresses due to the structural effect known as warping. Proper consideration of this complex topic requires an appreciation of the theory of torsion which is outside the scope of this lecture. In many cases torsional effects can be minimised by careful detailing such that load is transferred into members in a way that avoids twisting.

9. CONCLUDING SUMMARY

• The main design requirement for beams is the provision of adequate bending strength. The types of member normally used to achieve this have been indicated. Means of recognising beams whose design can be based on relatively simple structural principles have been presented.
• Section modulus, either elastic or plastic depending upon the design philosophy adopted, is the most appropriate property for use in selecting a suitable section.
• Shear capacity and deflection must also be checked in simple beam design.
• Situations in which a more complex structural response occurs, resulting in the need to consider biaxial bending, torsion, etc.., have been discussed.

10. REFERENCES

[1] Eurocode 3: " Design of Steel Structures": ENV 1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.

11. ADDITIONAL READING

1. Dowling, P.J., Owens, G.W. and Knowles, P., "Structural Steel Design", Butterworths, 1988.
2. Petersen C., "Stahlbauten", Vieweg Verlog Braunshweig, 1988.
3. Galambos, T.V., "Structural Members and Frames", Prentice-Hall, Englewood Cliffs, 1968.
4. Narayanan, R., "Beams and Beam Columns - Stability and Strength", Applied Science, London, 1983.
5. Salmon, C. G. and Johnson, J. E., "Steel Structures - Design and Behaviour", Harper and Row, New York, 1980.

TABLE 1

Previous | Next | Contents