Previous | Next | Contents

Lecture 7.10.3: Beam Columns III

OBJECTIVE/SCOPE

To describe the methods of beam-column analysis, either by verification of a single member or by verification of the whole frame.

PREREQUISITES

Lecture 7.1: Methods of Analysis of Steel Structures

Lectures 7.10: Beam Columns

RELATED LECTURES

Lecture 6.2: General Criteria for Elastic Stability

Lecture 7.3: Local Buckling

RELATED WORKED EXAMPLES

Worked Example 7.10: Beam Columns

SUMMARY

This lecture explains the basic methods of beam - column verification; this is done firstly for an isolated member, taking the end deformations and end forces from a global analysis of the whole frame and calculating the resistance using the rules given in Eurocode 3 [1]. The case where the member cannot be isolated from the frame structure is also covered by giving an alternative procedure, which yields an overall slenderness, , of the frame (including lateral-torsional buckling effects) that allows for frame verification using the European buckling curves.

1. INTRODUCTION

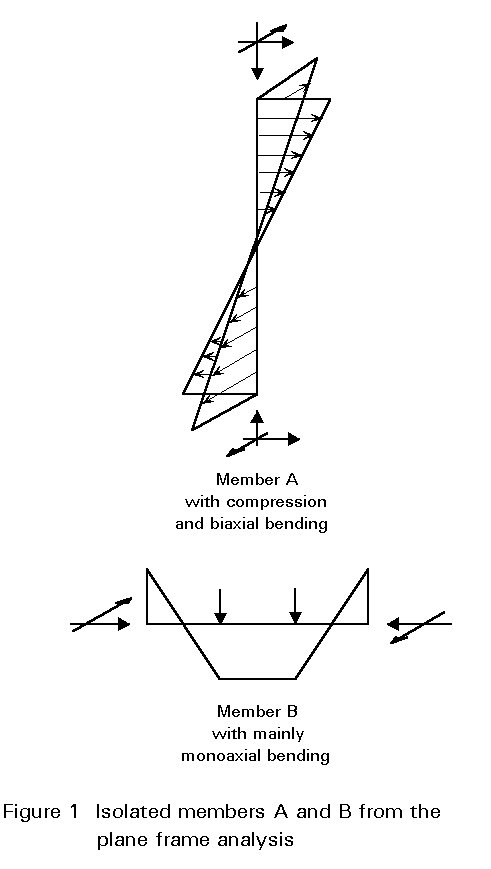
Normally, the design of an individual member in a frame is done by separating it from the frame and dealing with it as an isolated substructure. The end conditions of the member should then comply with its deformation conditions, in the spatial frame, in a conservative way, e.g. by assuming a nominally pinned end condition, and the internal action effects, at the ends of the members, should be considered by applying equivalent external end moments and end forces, Figure 1. Methods of verification for these members are given in Section 2.

A more general procedure is given in Section 3, for the case where members cannot be isolated from the frame structure in the way described above.

2. METHODS OF VERIFICATION FOR ISOLATED MEMBERS

2.1 Beam-columns with Mono-axial Bending only

For the design of beam-columns, with mono-axial bending only, two checks must be carried out:

• the in-plane buckling check taking into account the in-plane imperfections.
• the out-of-plane buckling check, including the lateral-torsional buckling verification that takes account of the out-of-plane imperfections (see Figure 2).

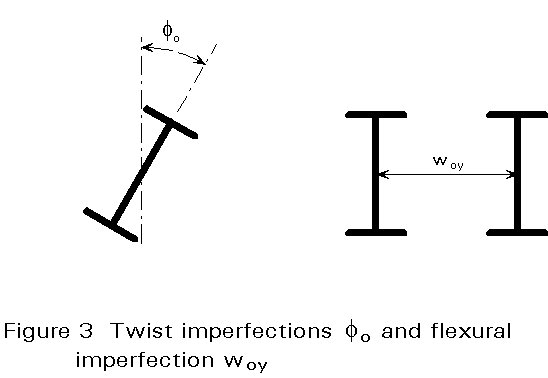
It has been found by test calculations that twist imperfections, r, of beam-columns that are susceptible to lateral-torsional buckling, can be substituted by flexural imperfections, see Figure 3.

Members with sufficient torsional stiffness, e.g. hollow section members, need not be verified for lateral-torsional bucking.

The in-plane or out-of-plane flexural buckling check is done using the interaction formula:

where c_min is the lesser of c_y and c_z and the factor k_y is given by:

k_y = 1 -  (m_yN_Sd)/(c_y Af_y) £ 1,5

where:

m_y =  _y{2b_My - y + (W_ply - W_ely)/W_ely} £  0.90

b_My takes account of the shape of the moment distribution diagram between the member ends. Values for this are given in Table 1.

In the case where lateral-torsional buckling is possible, the verification must be carried out using the following formula:

where c_z refers to the direction of the lateral-torsional buckling.

c_LT is the relevant reduction factor for lateral-torsional buckling

k_LT =

where:

m_LT = 0,15 _z b_M - 0,15 £ 0,90

and b_M is given by Table 1.

When the non-dimensional slenderness _LT £ 0,4, the reduction coefficient c_LT need not be taken into account. This rule may be used for spacing the lateral restraints to resist lateral-torsional buckling.

The above verification formulae are valid for members with Class 1 and Class 2 sections; in the case of Class 3 sections, W_pl must be substituted by W_el; in the case of Class 4 sections, reference should be made to Lecture 7.3.

2.2 Beam-columns with Bi-axial Bending

In the case of beam-columns with bi-axial bending, the formulae given in Section 2.1 have to be expanded.

The interaction without lateral-torsional buckling becomes:

The interaction with lateral-torsional buckling reads:

The definition of k_z and W_plz are analogous to those for k_y and W_ply, given in the previous Section.

Figure 4 illustrates these interactive formulae.

3. METHOD OF VERIFICATION OF WHOLE FRAMES

3.1 General

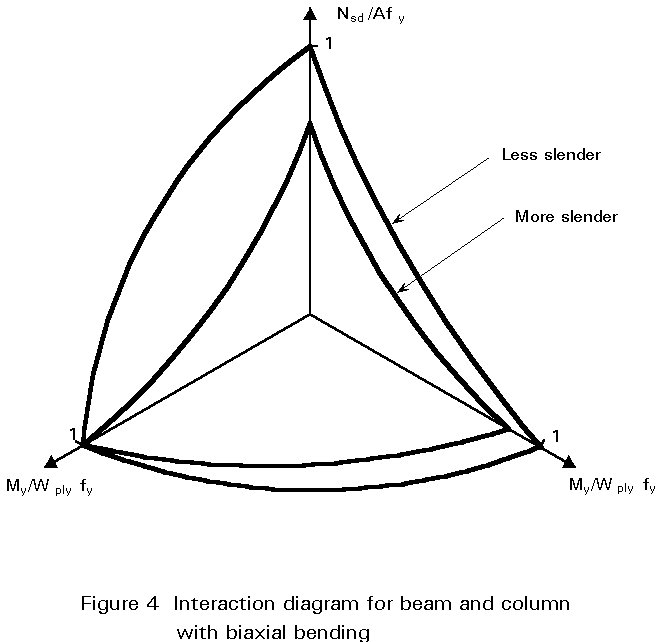
Figure 5 gives an example of a portal frame with tapered columns and beams, the external flanges of which are laterally supported by the purlins which, due to their flexural stiffness, also provide torsional restraint; the beams and columns may, however, be subject to distortion of the cross-section, due to the flexibility of the web.

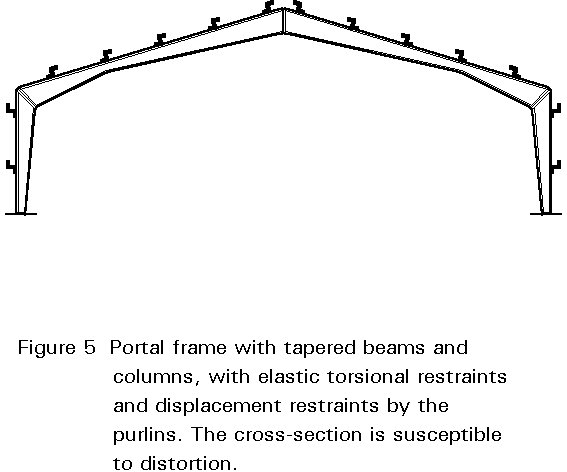
An accurate verification of this arrangement should be based on a finite element model which takes the above effects into account. The basic assumptions made regarding the imperfections in this model, would be such that the standard verification given in Section 2 would produce equally favourable results since the standard procedure has been calibrated against test results.

A more simplified procedure is, therefore, given here which is related to the verification of columns for flexural buckling, and beams for lateral-torsional buckling.

3.2 Basic Assumption

The basic principles governing the standard verification of columns for flexural buckling, and beams for lateral-torsional bucking, are as follows:

1. The non-dimensional slenderness is defined by:

_{FB =} Ö{N_pl/N_cr);  _{LT =} Ö{M_pl/M_cr)

where N_pl, M_pl are the characteristic values of the elastic/plastic resistances of the column or beam neglecting any out-of-plane effects; and N_crit, M_crit are the critical bifurcation values for the column resistance, or the beam resistance, when considering out-of-plane deflections and hyperelastic behaviour in the equilibrium state.

2. Using the non-dimensional slenderness, , a reduction factor c can be determined from the European buckling curves that allows the design value of the resistance of the column or beam to be defined by:

N_bd = c N_pl / g_M1 for the column

M_bd = c M_pl / g_M1 for the beam.

In applying this principle to any loaded structure, see Figure 6, the procedure is as follows:

1. As a first step the structure is analysed for a given load case with an elastic or plastic analysis assuming that any out of plane deflections are prevented. By this analysis a multiplier, g_pl, of the given loads is found that represents the ultimate resistance of the structure.
2. The structure is then checked assuming hyperelastic material behaviour allowing for lateral and torsional deflections. This leads to a multiplier g_crit of the given loads that represents the critical elastic resistance of the structure to lateral buckling or lateral-torsional bucking.
3. The overall slenderness, , of the structure can then be defined by:

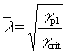
and by using the reduction coefficient c from the relevant European buckling curve, e.g. curve c, the final safety factor:

g = c g_pl

can be derived.

This procedure is analogous to the Merchant-Rankine procedure for the non- elastic verification of frames.

3.3 Tools for the Procedure

In general the procedure described in Section 3.2 needs a computer program that performs a planar elastic-plastic analysis of the frame and determines the elastic bifurcation load of the structure for lateral and torsional deflections, including distortion. Such a program, for calculating the elastic bifurcation loads, can either be based on finite elements or on a grid model where the flanges and stiffeners are considered as beams and the web is represented by an equivalent lattice system that allows for second order effects; such programs are available on PC's.

4. CONCLUDING SUMMARY

• A three dimensional frame may generally be analysed by separating it into plane frames and analysing these on the assumption of no imperfections; the individual members of the frame should then be checked with the imperfection effects taken into account.
• The isolated members in general represent beam-columns with either inplane or biaxial bending.
• Beam - columns with mono-axial bending, which are not susceptible to lateral-torsional buckling, e.g. hollow sections, shall be verified for inplane and out of plane buckling by means of an interaction formulae.
• In the case of beam-columns which are susceptible to lateral-torsional buckling the out of plane flexural buckling of the column has to be combined with the lateral-torsional buckling of the beam using the relevant interaction formulae.
• For beam-columns with biaxial bending, the interaction formula is expanded by the addition of an analogous term.
• In certain cases the standard procedure for the verification of a beam- column is not applicable and more accurate models must be used.
• As a non-linear spatial analysis including the effect of imperfections is difficult, an alternative procedure is provided by which the overall slenderness of a frame is defined; this allows verification of the frame using the European buckling curves which take account of lateral- torsional buckling. This procedure is analogous to the Merchant-Rankine procedure.

5. REFERENCES

[1] Eurocode 3: "Design of Steel Structures": ENV1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.

6. ADDITIONAL READING

1. Eurocode 3 - Background Document 5.05 "Design rules for thin-walled plate girders for the ultimate and serviceability limit state taking account of the buckling phenomena". Part A: Results Eurocode 3 Editorial Group CEC 1991.
2. Braham M. et al: Ein alternatives Verfabren zur Bestimmung der Biegedrillknicksicherheit von Konstruktionen. Der Stahlbau 1992.