Previous | Next | Contents

Lecture 12.4.2: Fatigue Behaviour of

Hollow Section Joints II

OBJECTIVE/SCOPE:

To give information for the design of hollow section joints with guidelines for an optimal design.

PRE-REQUISITES

Lecture 12.1: Basic Introduction to Fatigue

Lecture 12.3: Effect of Workmanship on Fatigue Strength of Longitudinal and Transverse Welds

Lecture 13.1: Application of Hollow Sections in Steel Structures

Lecture 13.2: The Behaviour and Design of Welded Connections Between Circular Hollow Sections under Predominantly Static Loading

Lecture 13.3: The Behaviour and Design of Welded Connections Between Rectangular Hollow Sections under Predominantly Static Loading

RELATED LECTURES

Lecture 12.4.1:Fatigue Behaviour of Hollow Section Joints I

SUMMARY

The geometric stress concept and the classification method used for the fatigue design of hollow section joints are discussed in more detail and illustrated by design examples. Guidelines and simplified design graphs are given to give insight into the stress concentration factors to stimulate optimal design.

The limitations and the validity of various approaches are also discussed.

NOTATION

The notation of Eurocode 3 has been adopted.

1. INTRODUCTION

In Lecture 12.4.1, the fatigue behaviour of hollow section joints and methods of analyses are discussed. In Eurocode 3, two methods are adopted for the design of hollow section joints [1].

The geometric stress method (sometimes called the hot spot stress method) can generally be used for all types of connections between hollow sections. However, sufficient data regarding stress concentration factors for various types of joints and loadings are required.

The classification method also given in Eurocode 3 for K- and N-type joints with wall thicknesses up to 12,5 mm is a simplified method, only valid for a particular range of geometrical parameters.

In this lecture these two methods are discussed in more detail and the method of design is given.

2. MODELLING OF THE STRUCTURE

For fatigue design, the stress ranges in the members have to be known. The stresses determined depend directly on the idealization of the structure.

Trusses made of hollow sections generally have welded connections with continuous chords. For ease of fabrication the diagonals are sometimes connected with a certain noding eccentricity e, see Figure 1.

To obtain the correct load and stress distribution in the members, there are various methods of modelling [2].

a. The best method is to model the connections as substructures, as shown in Fig. 11 of Lecture 12.4.1. In this way, the influence of the geometry of the connections is directly taken into account. Even the governing extrapolated geometric stresses at the weld toes can be determined directly. However, this method requires excellent pre- and post-processors for the finite element modelling and sufficient computer capacity. Only specialized research institutes and companies can handle this method at present. Furthermore, the designer who is modelling should be a specialist in the use of the correct elements and the correct meshes.

b. Another method is to use parametric formulae to determine the connection stiffness. The truss is then modelled with continuous chords and the diagonals are connected by springs representing the connection stiffness to the chord. Eccentricities should be incorporated in the model. In this way the proper bending moments in the members can be determined. The axial load distribution in the members is hardly influenced by the modelling, e.g. pin, spring or rigidly connected diagonals, see Figure 2. For bending moments, however, considerable differences may occur, since the actual bending stiffness is influenced by the axial loads present (interaction). In offshore engineering it is common practice to assume rigidly connected members. However, the value of the bending moments is reduced by taking not the moments at the noding points but those at the chord face. Due to a lack of evidence of the stiffness characteristics and for simplicity this simplification is used.

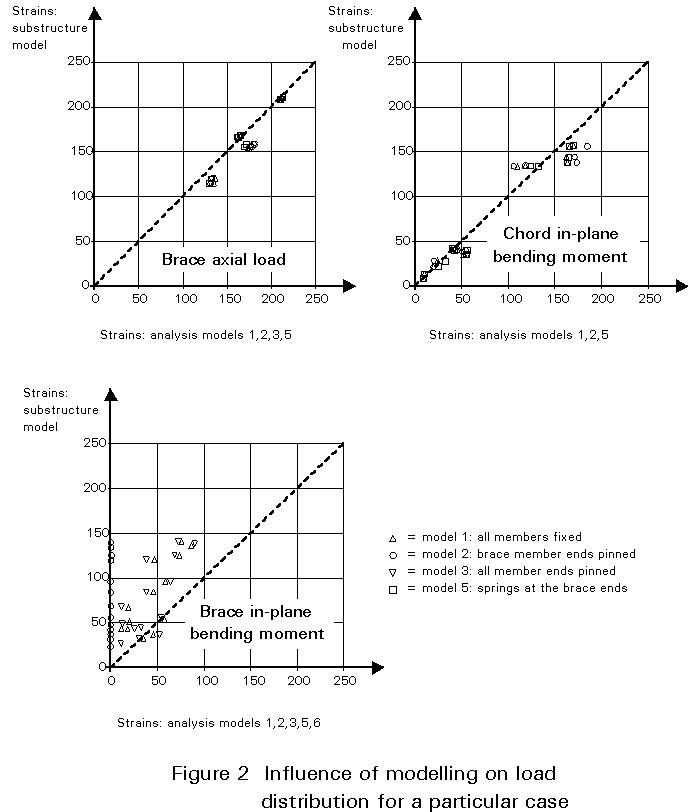
c. The simplest method of modelling is to use continuous chords with the diagonals connected with pins to the chord. Eccentricities exceeding 0,55 (d_o or h_o) £ e £ 0,25 (d_o or h_o) should be incorporated as shown in Figure 3.

The effect of secondary bending moments should be included by multiplying the stress ranges due to axial forces by the factors given in Tables 1a and 1b of Lecture 12.4.1.

This simplified modelling assumes indirectly that the stress concentration factors for bending are similar as those for axial forces, which is not generally valid. The stress concentration factors for bending in-plane are generally lower than those for axial force.

There are of course other methods of modelling, but those mentioned above represent the most commonly used ones.

3. END-TO-END CONNECTIONS AND ATTACHMENTS

End-to-end connections and connections with plates and hollow sections with attachments are classified in the normal way, i.e. a fatigue class is given for 2 ´ 10⁶ cycles as shown in Table 1. Here a slope constant of m = 3 is adopted for N £ 5 ´ 10⁶. For spectrum loading, a slope constant of m = 5 is adopted for 5 ´ 10⁶ to the cut off limit 10⁸. It should be noticed that for end-to-end connections an opposite "thickness effect" is included. In these connections no or only small geometrical effects are present, causing the crack to initiate from the root of the weld. Since these welds are made from one side (not counter welded) the root effect is more severe for smaller thicknesses. Here the limit is taken at 8 mm. For thicknesses larger than 25 mm the normal thickness effect should be applied, i.e.

 Ds_t = Ds_t=25[t/25]^-0,25                            (1)

4. GEOMETRIC STRESS METHOD

4.1 Reference Curves

The basic reference curves for 16 mm wall thickness, according to Eurocode 3 [1] are given in Figure 4. The equations for the reference curves and the thickness effects to be adopted are also given.

As discussed in Lecture 12.4.1, for hollow section joints with partial penetration welds or fillet welds, sufficient evidence is now available to use the same curves as for full penetration butt welds.

4.2 Determination of Geometric Stresses by F.E. Modelling

The geometric stress should be determined by extrapolation of the geometric stress outside the influence region of the weld to the weld toe. For most connections of circular hollow sections the geometric stress has a linear part and a linear extrapolation can be used as shown in Figure 5a.

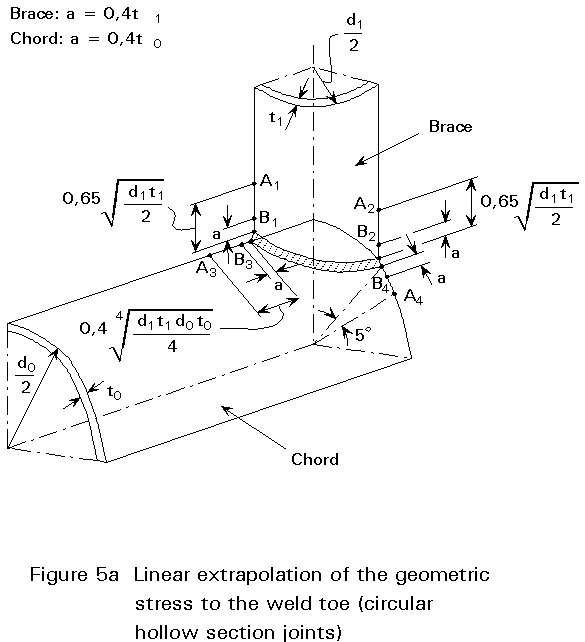
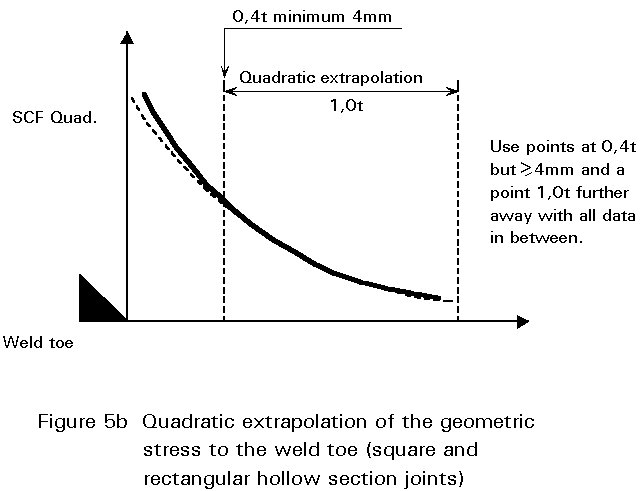
For square or rectangular hollow section joints the geometric stress is non-linear and a quadratic extrapolation gives a better accuracy and lower scatter in test results, Figure 5b. This extrapolation is more consistent with the mode of failure (location of the crack).

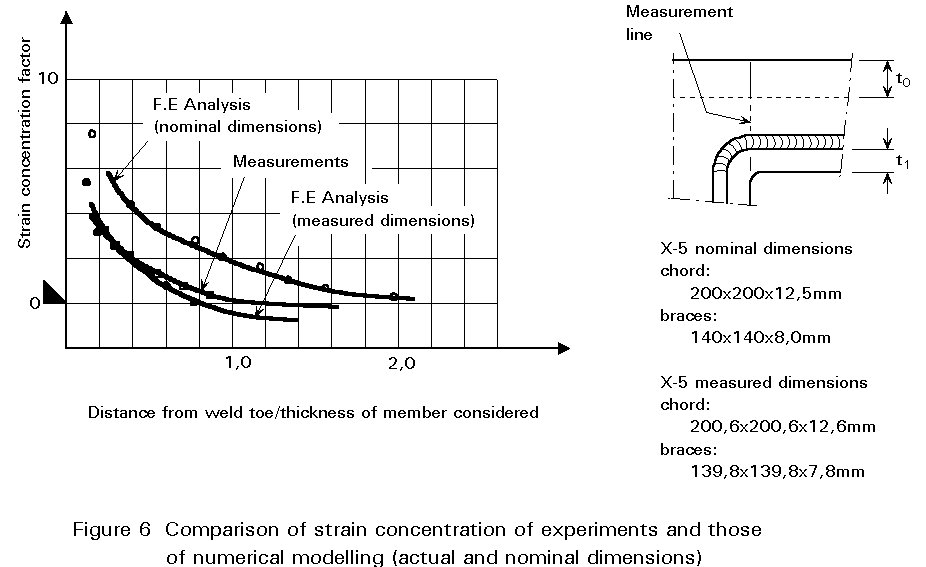
Determination of the geometric stresses by F.E. modelling requires proper modelling (type of elements, mesh), preferably by methods which have been calibrated by tests [2]. Due to the difference between actual dimensions and nominal dimensions, the calibration should be done with care using the actual dimensions, see Figure 6.

4.3 Stress Concentration Factors

The geometric stress can also be obtained by multiplying the nominal stresses by the relevant stress concentration factors. Many parametric formulae are now available for circular hollow section joints. The most extensive set which gives good agreement with measurements is given by Efthymiou [3]. For square hollow section joints, a set of parametric formulae for T- and X-joints is given by Van Wingerde [4]. For K- and N-joints of square hollow sections, formulae are available, however only for a particular combination of axial loads and bending moments [5]. Thus, they are not generally applicable. Currently, new parametric formulae are being developed in the framework of a CIDECT programme. These formulae will become available in 1994.

To give formulae for all types of joints, for various locations and for various loadings is beyond the scope of this lecture. However, some graphical presentations are given in Figures 7 - 15 for circular hollow section joints and in Figures 16 - 18 for T- and X-joints of square hollow sections. If the effect of the stiffness distribution along the intersection perimeter is clearly understood, then the tendency of the graphs will be clear. All graphs show that the SCF for the saddle location achieves a maximum for medium ß ratios. For T- and X-joints minimum values are obtained for ß = 1,0. Here, the SCF changes very rapidly for small variations of ß. For this reason, for X-joints of circular hollow sections, lower values than those for ß = 0,95 are not taken, because for ß= 1,0 the weld might cause an eccentricity.

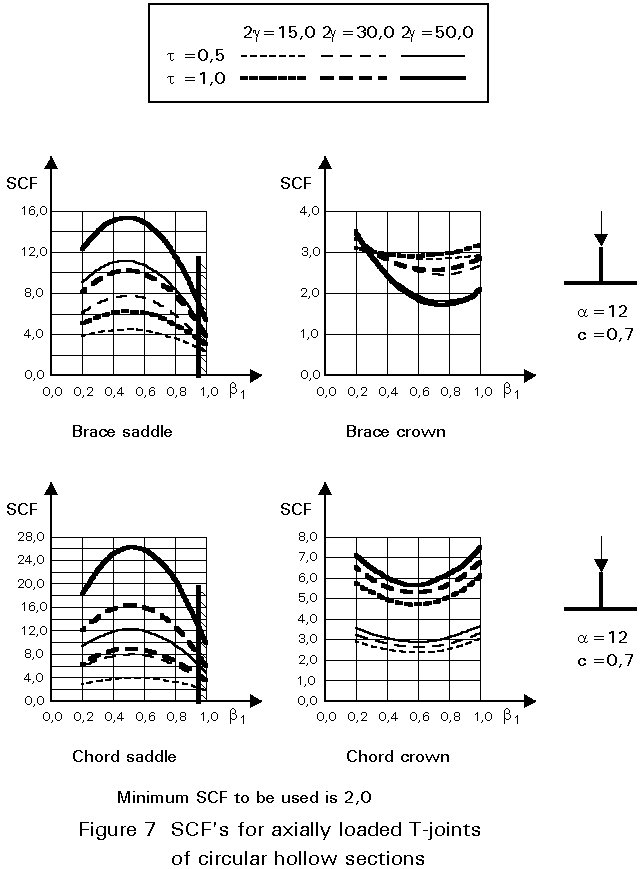
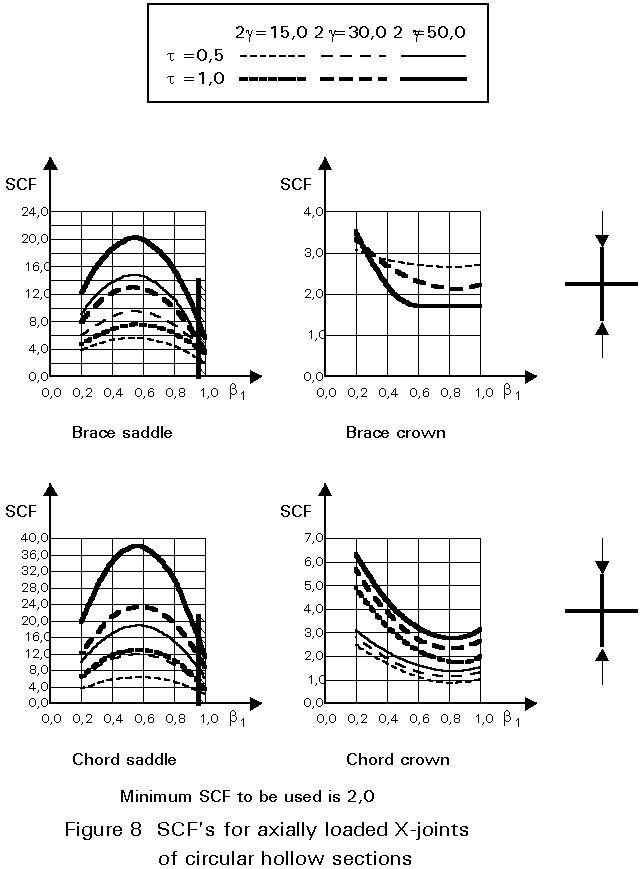
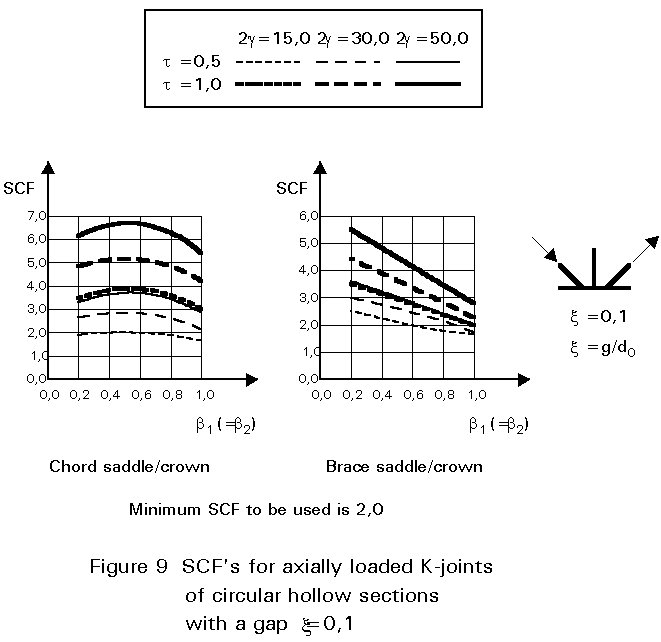
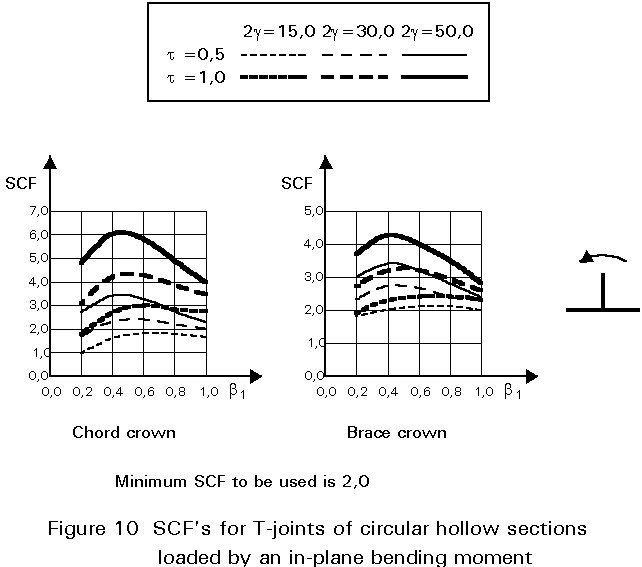
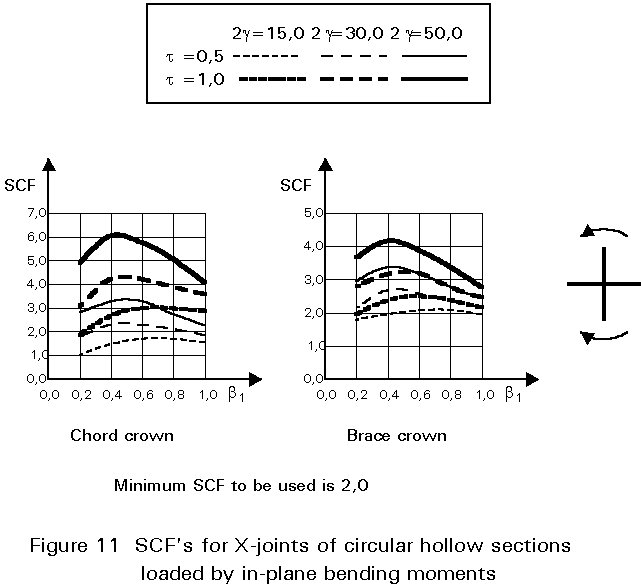
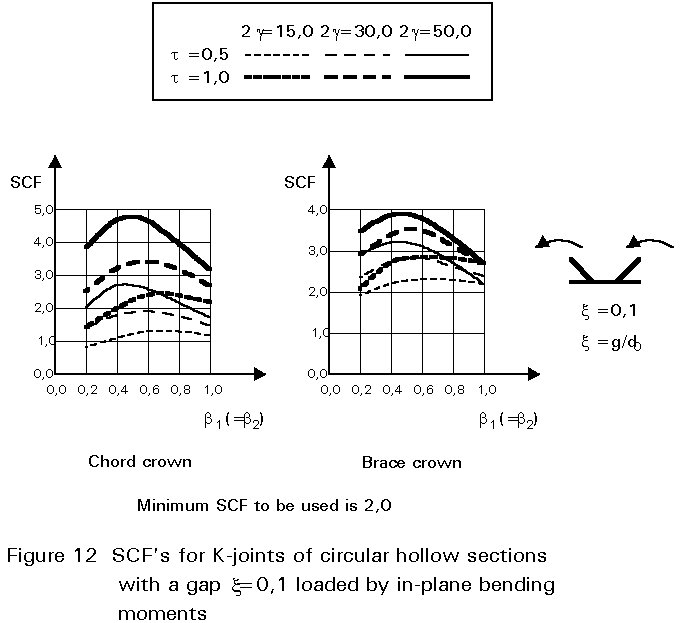
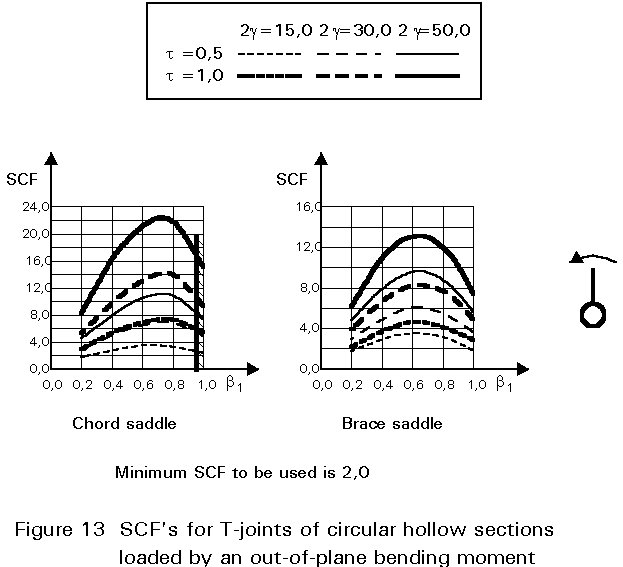
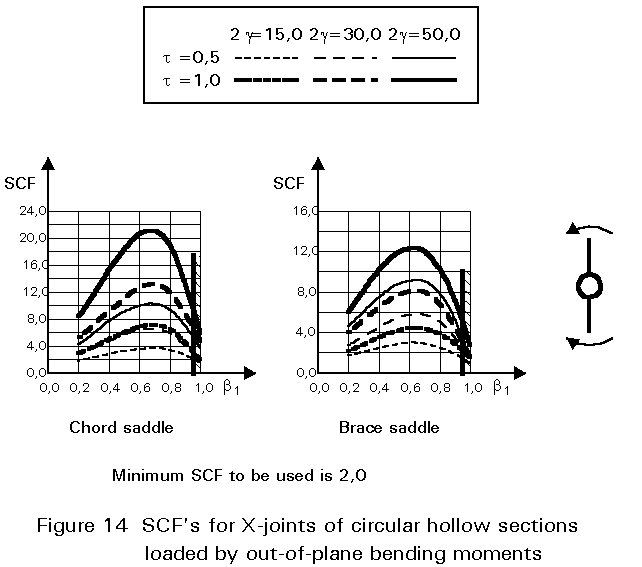
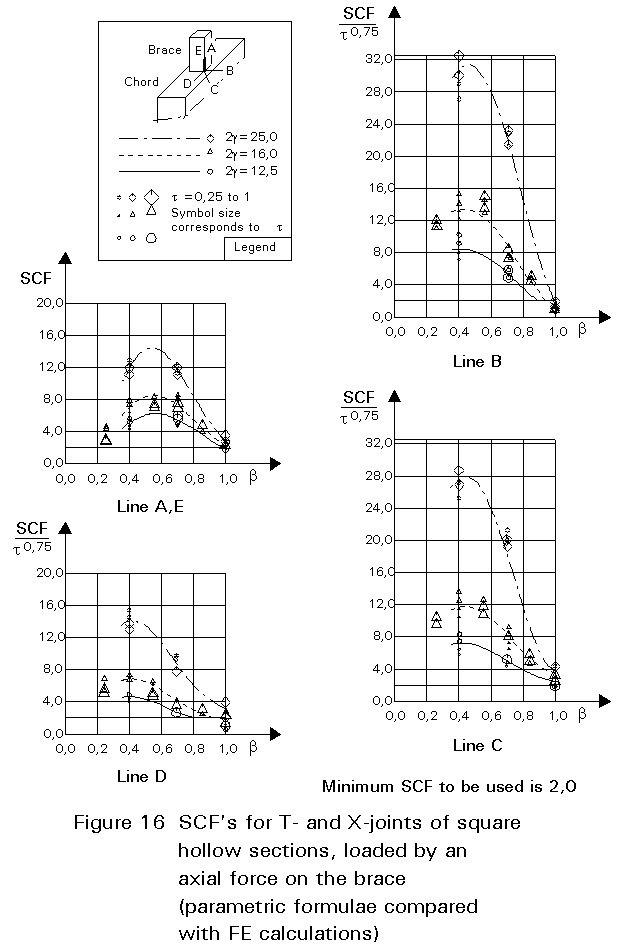
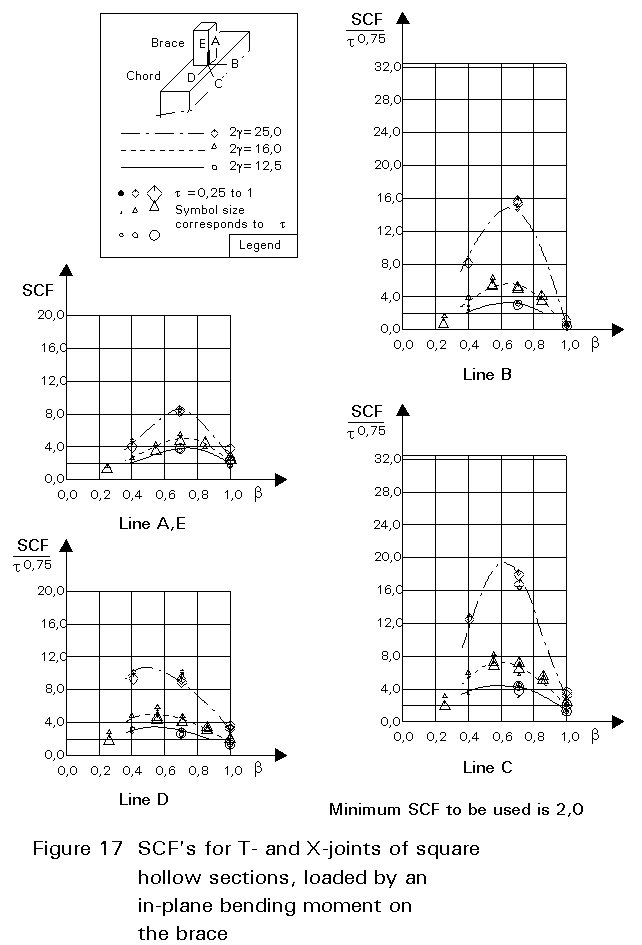
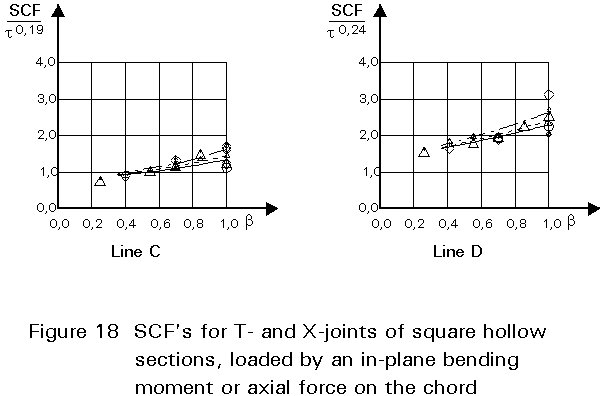
Note that the effect of the bending moment in the chord in a T-joint is included in the SCF's for T-joints of circular hollow sections, whereas for T-joints of square hollow sections it has been excluded, allowing the same presentation as for X-joints.

It is recommended that a minimum stress concentration factor of 2 is adopted to cover cracking from the root of the weld. Furthermore, the SCF's should be multiplied by the following correction factors for square hollow section joints if fillet welded connections are used:

Brace: 1,4 (for lines A and E)

Chord: 1,0 (no correction factors)

These factors cover the effect of brace wall bending. For the chord, the weld toe is located further away from the brace, resulting in a lower SCF. However, insufficient evidence is available yet to quantify this in general. Therefore, a factor 1,0 is adopted for the time being.

For an optimal design the geometric stress concentration factors should be low, i.e. low t and g values and low ß or high ß values.

As indicated in Lecture 12.4.1, the geometric stress range can be obtained by multiplying the relevant stress concentration factor (location and loading) by the nominal stress range, which causes the stress peak.

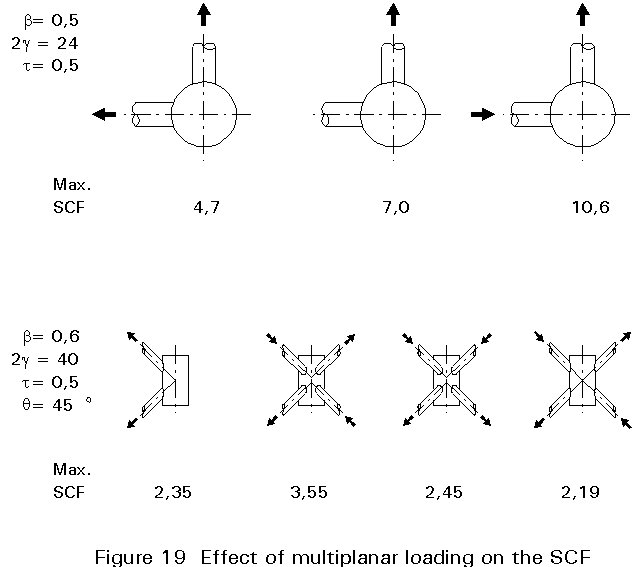
Care has to be taken that the stress concentration factors are only used within the range of validity. Figure 19 shows, for example, that the effect of multiplanar loading can be considerable.

4.4 Fatigue Life

The fatigue life is determined by checking the highest geometric stress for the chord as well as for the brace multiplied by the appropriate g_M factor with the basic Ds-N curve using the appropriate thickness.

5. CLASSIFICATION METHOD

The classification method is only used for axially loaded K- and N-type joints of circular and rectangular hollow sections, since the variation in SCF is too large for other types of joints.

In principle, the classes should be a lower bound, defined by the basic reference curve for the geometric stress range divided by the SCF's which can be obtained within the range of validity. The classification is based on an analysis of relevant test results, taking account of the parameter t and using a lower bound. In this approach, the effects of other influencing parameters and the thickness effects are combined to some extent.

Multiplication of the class by a minimum SCF of 2,0 gives values far exceeding those of the basic reference curve for geometric stress, even if the thickness effect is incorporated. On the other hand, the two approaches cannot be compared directly, since the slopes are different, i.e. for the classification method a fixed slope constant of m = 5 is adopted.

Although Eurocode 3 [1] gives the range of validity shown in Table 1, it would be better to change some of the limits, i.e.

4 £ t_o or t₁ £ 8 mm instead of t_o or t₁ £ 12,5 mm

b_o/t_o × t₁ or d_o/t_o × t₁ £ 100 instead of b_o/t_o or d_o/t_o £ 25

These limits are in better agreement with the test results on which this classification method has been based.

In view of these comments, one could ask: "Why has the classification method been adopted?" At the time of drafting Eurocode 3, insufficient evidence was available for SCF's of hollow section joints. Further, many designers are not familiar with the geometric stress concept. Therefore the classification method was favoured by many countries.

The design is very simple, since the designer determines the nominal stress ranges in the brace with one of the methods described in Section 2 considering the factors for secondary bending moments and the relevant g_M factor. The design class gives the Ds-N curve and the fatigue life can be determined.

6. GENERAL REQUIREMENTS FOR WELDING

The connections at the welded joints should be made over the entire perimeter of the hollow sections by means of a full penetration weld, partial penetration weld, fillet weld, or a combination. Full penetration welds should be used if:

• The brace has a wall thickness larger than 8 mm.
• The angle at the toe of the brace is larger than 120° .
• For joints between square or rectangular hollow sections with ß = 1,0, fillet welds can only be used at the side of the brace perpendicular to the axis of chord. Therefore, the sides parallel to the chord axis should be welded by a full penetration butt weld.

Attention should be paid to the proper selection of materials and the welding procedure. To avoid failure of the weld under static loading, the throat thickness of the fillet weld for steel up to S355 is equal to or greater than the wall thickness of the brace (a ³ t₁).

Welding should start at the middle of the sides. If welding of joints commences at the corners of the brace, the fatigue strength deteriorates. This may result in a decrease by a factor 2 on stress range.

7. CONCLUDING SUMMARY

For the geometric stress method and the classification method:

• The modelling of the structure should be done with care, considering secondary bending moment effects.
• In using F.E. modelling, proper consideration of elements and meshes is required, as well as calibration with test results. The geometric stresses should be extrapolated to the weld toe in a standardized manner.
• Stress concentration factor formulae should be used within their range of validity. For example the formulae for uniplanar joints cannot be used for multiplanar loading.
• Fillet welds exhibit higher SCF's in the brace than butt welds.
• For axially loaded T- and X-joints the highest SCF's occur for medium ß ratios (0,5 to 0,6)
• The classification method and the geometric stress approach are not yet consistent.
• Welding of hollow section joints should not start at the locations of high stress concentrations, e.g. not at the corners of rectangular or square hollow sections, but at the middle of the sides.

8. REFERENCES

[1] Eurocode 3: "Design of Steel Structures": ENV 1993-1-1: Part 1, General rules and rules for buildings, CEN, 1992.

[2] Romeijn, A., Puthli, R.S., Wardenier, J.: "Finite element modelling of multiplanar joint flexibility in tubular structures", Proceedings ISOPE '92, San Francisco, U.S.A.

[3] Efthymiou, M.: "Development of SCF formulae and generalised influence functions for use in fatigue analysis", Offshore Tubular Joints Conference (OTJ '88), UEG Offshore Research, Englefield Green Near Egham, U.K., 1988.

[4] Van Wingerde, A.M.: "The fatigue behaviour of T- and X-joints made of square hollow sections", Ph.D. thesis, Delft University of Technology.

[5] Mang, F., Herion, S., Bucak, Ö., Dutta, D.: "Fatigue behaviour of K-joints with gap and with overlap made of rectangular hollow sections", p. 297-310 of Proceedings "Tubular Structures", edited by E. Niemi and P. Mäkeläinen.

9. ADDITIONAL READING

1. Dutta, D., Mang, F., Wardenier, J.: "Fatigue behaviour of welded hollow section joints", CIDECT Monograph No. 7.
2. "Design of tubular joints for offshore structures", vol. 1, 2 and 3, UEG publication UR33.
3. Romeijn, A., Puthli, R.S., Wardenier, J.: "The flexibility of uniplanar and multiplanar joints made of circular hollow sections", Proceedings ISOPE '91, Edinburgh, U.K.

Table 1 Detail category: Hollow sections and simple connections

Fig T1-1

Fig T1-2

Fig T1-8

Fig T1-9

Fig T1-10

Fig T1-11

Fig T1-12

Fig T1-13

Fig T1-14

Fig T1-15

Fig T1-16

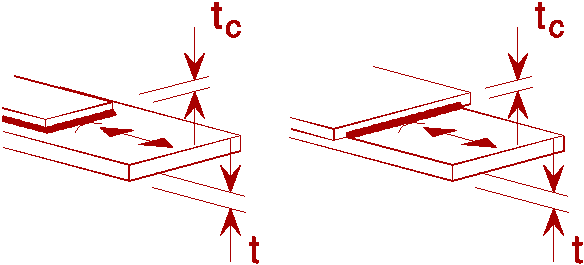
Table 2: Classes for classification method

Detail categories for lattice girder joints
Detail category m = 5	Construction Details		Description
90	to/ti ³ 2,0	See Fig T2-1	Joints with gap Circular hollow sections, K and N joints
45	to/ti ³ 1,0
71	to/ti ³ 2,0	See Fig T2-2	Joints with gap Rectangular hollow sections, K and N joints Requirements × 0,5(bo-bi) £ g £ 1,1(bo-bi) × g ³ 2to
36	to/ti ³ 1,0
71	to/ti ³ 1,4	See Fig T2-3	Joints with overlap K joints Requirements × overlap between 30% and 100%
56	to/ti ³ 1,0
71	to/ti ³ 1,4	See Fig T2-4	Joints with overlap N joints
50	to/ti ³ 1,0
General Requirements to, ti £ 12,5 mm 35° £ Q £ 50° bo/to £ 25 0,4 £ bi/bo £ 1,0 0,25 £ di/do £ 1,0 bo/to £ 25 bo £ 200 mm do £ 300 mm -0,5do £ e £ 0,25do -0,5ho £ e £ 0,25ho Out-of-plane eccentricity: £ 0,02bo or £ 0,02do Fillet welds are permitted in braces with wall thicknesses £ 8 mm

Table 2: Classes for classification method

• For intermediate t_o/t_i values, use linear interpolation between nearest detail categories
• Note that the braces and the chords require separate fatigue assessments

Note regarding General Requirements:

Preferably use 4 £ t_o or t₁ £ 8 mm instead of £ 12,5 mm

Preferably use b_o/t_o × t₁ or d_o/t_o × t₁ £ 100 mm instead of b_o/t_o or d_o/t_o £ 25

Fig T2-1

Fig T2-2

Fig T2-3

Fig T2-4

Previous | Next | Contents