ESDEP WG 8
PLATES AND SHELLS
To describe the basic characteristics of pre- and post-buckling shell behaviour and to explain and compare the differences in behaviour with that of plates and bars.
Lecture 8.6: Introduction to Shell Structures
Lecture 6.1: Concepts of Stable and Unstable Elastic Equilibrium
Lecture 8.1: Introduction to Plate Behaviour and Design
Lecture 8.4.1: Plate Girder Behaviour & Design I
Lectures 8.5.1: Introduction to Design of Box Girders
The combined bending and stretching behaviour of shell structures in resisting load is discussed; their buckling behaviour is also explained and compared with that of struts and plates. The effect of imperfections is examined and ECCS curves, which can be used in design, are given. Reference is also made to available computer programs that can be used for shell analysis.
Lecture 8.6 introduced several aspects of the structural behaviour of shells in an essentially qualitative way. Before moving on to consider design procedures for specific applications, it is necessary to gain some understanding of the possible approaches to the analysis of shell response. It should then be possible to appreciate the reasoning behind the actual design procedures covered in Lectures 8.8 and 8.9.
This Lecture, therefore, presents the main principles of shell theory that underpin the ECCS design methods for unstiffened and stiffened cylinders. Comparisons are drawn with the behaviour of columns and plates previously discussed in Lectures 6.6.1, 6.6.2 and 8.1.
The deformation of an element of a thin shell consists of the curvatures and normal displacements associated with out-of-surface bending and the stretching and shearing of the middle surface. Bending deformation without stretching of the middle surface, as assumed in the small deflection theory for flat plates, is not possible, and so both bending and stretching strains must be considered.
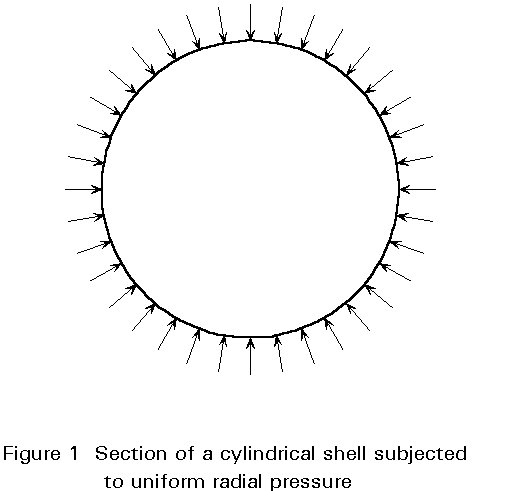
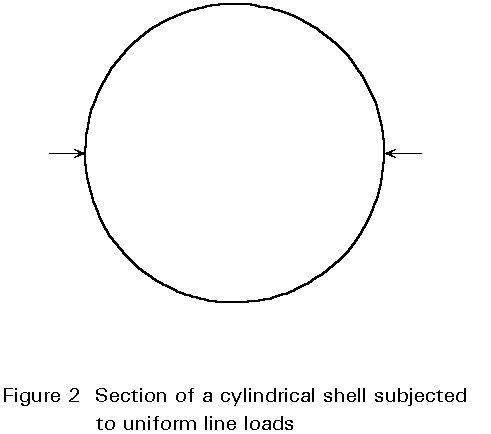
If the shape and the boundary conditions of a shell and the applied loads are such that the loads can be resisted by membrane forces alone, then these forces may be found from the three equilibrium conditions for an infinitely small element of the shell. The equilibrium equations may be obtained from the equilibrium of forces in three directions; that is, in the two principal directions of curvature and in the direction normal to the middle surface. As a result, the three membrane forces can be obtained easily in the absence of bending and twisting moments and shear forces perpendicular to the surface. An example is an unsupported cylindrical shell subjected to uniform radial pressure over its entire area (Figure 1). Obviously, the only stress generated by the external pressure is a circumferential membrane stress. The assumption does not hold if the cylinder is subjected to two uniform line loads acting along two diametrically opposed generators (Figure 2). In this case, bending theory is required to evaluate the stress distribution, because an element of the shell cannot be in equilibrium without circumferential bending stresses. Circumferential bending stresses are essential to resist the external loads, and because the wall is thin and has very little flexural resistance, they greatly affect its load carrying resistance [1].

Significant bending stresses usually only occur close to the boundaries, or in the zone affected by other disturbances, such as local loads or local imperfections. Locally, the resulting stresses may be quite high, but they generally diminish at a small distance from the local disturbance. Bending stresses may, however, cause local yielding which can be very dangerous in the presence of repeated loadings, since it can result in a fatigue fracture.
It is normally more structurally efficient if a shell structure can be configured in such a way that it carries load primarily by membrane action. Simpler design calculations will usually also result.
Buckling may be regarded as a phenomenon in which a structure undergoes local or overall change in configuration. For example, an originally straight axially loaded column will buckle by bowing laterally; similarly a cylinder may buckle when its surface crumples under the action of external loads. Buckling is particularly important in shell structures since it may well occur without any warning and with catastrophic consequences [2-4].
The equations for determining the load at which buckling is initiated, through bifurcation on the main equilibrium path of a cylindrical shell, may be derived by means of the adjacent equilibrium criterion, or, alternatively, by use of the minimum potential energy criterion. In the first case, small increments (u1, v1, w1) are imposed on the pre-buckling displacements (u0, v0, w0)
u = u0 + u1
v = v0 + v1 (1)
w = w0 + w1
The two adjacent configurations, represented by the displacements before (u0, v0, w0) and after the increment (u, v, w) are analysed. No increment is given to the load parameter. The function represented by (u1, v1, w1) is called the buckling mode. As an alternative, the minimum potential energy criterion can be adopted to derive the linear stability equations. The expression for the second variation of the potential energy of the shell in terms of displacements is calculated. The linear differential equations for loss of stability are then obtained by means of the Trefftz criterion. Readers requiring a more detailed coverage of shell buckling are advised to consult [4].
In practice, for some problems, the results obtained by these analyses are adequate and in accordance with experiment. In other cases, such as the buckling of an axially compressed cylinder, the results can be positively misleading as they may substantially overestimate the actual carrying resistance of the shell. The use of these methods leads to the following value for the axial buckling load of a perfect thin elastic cylinder of medium length:
![]() (2)
(2)
Assuming n = 0,3 for steel gives scr = 0,605 E ![]()
This buckling load is derived on the assumption that the pre-buckling increase of the radius due to the Poisson effect is unrestrained and that the two edges are held against translational movement in the radial and circumferential directions during buckling, but are able to rotate about the local circumferential axis. These edge restraints are usually called "classical boundary conditions".
Equation (2) is of little use to the designer because test results yield only 15-60% of this value. The reason for the big discrepancy between theory and experimental results was not understood for a long time and has been the subject of many studies; it can be explained as follows:
The boundary conditions of the shells have a significant effect and can, if modified, give rise to lower critical loads. Many authors have investigated the effects of the boundary conditions on the buckling load of cylindrical shells. The value given by Equation (2) refers to a real cylinder only if the edges are prevented from moving in the circumferential direction, i.e. v = 0 (Figure 3). If this last condition is removed and replaced by the condition nxy = 0 (i.e. free displacement but no membrane stress in the circumferential direction) a critical value of approximately 50% of the classical buckling load is obtained. This boundary condition is quite difficult to obtain in practice and cylinders with such edge restraints are much less sensitive to imperfection than cylinders with classical boundary conditions; they are, therefore, not of primary interest to the designer. If, instead, the top edge of the cylinder is assumed to be free, the critical buckling load drops down to 38% of the critical value given by Equation (2). In general, it can be stated that if a shell initially fails with several small local buckles, the critical load does not depend to any great extent on the boundary conditions, but, if the buckles involve the whole shell, the boundary conditions can significantly affect the buckling load.
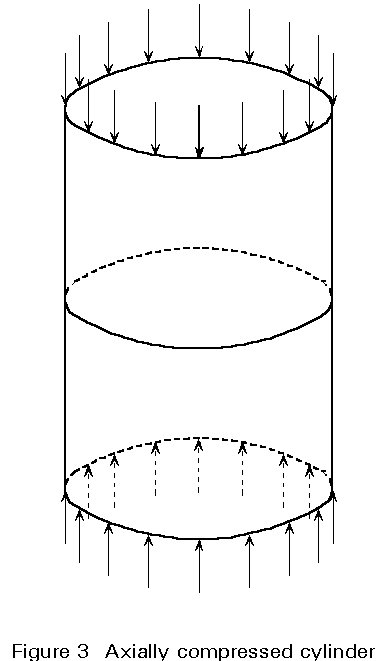
The critical buckling load may also be reduced by pre-buckling deformations. To take these deformations into account, the same boundary conditions in both the pre- and post-buckling range must be included. The consequence is that during the compression prior to buckling, the top and bottom edges cannot move radially (Poisson's ratio not being zero) and, therefore, the originally straight generators become curved. The post-buckling deformations are not infinitely small and the critical stress is reduced.
The complete understanding of the reason for the large discrepancies between theoretical and experimental results in the buckling of shells has caused much controversy and discussion, but now the explanation that initial imperfections are the principal cause of the phenomenon is generally accepted.
The starting point for this illustrative study of the post-buckling behaviour of a perfect cylinder, under axial compression (Figure 3), is Donnell's classical equations [2]. A suitable function for w (trigonometric) may be assumed and introduced into the compatibility equation, expressed in terms of w and of an adopted stress function F. The quadratic expressions can be transformed to linear ones by means of well known trigonometric relations. Then the stress function F, and as a consequence the internal membrane stresses, may be computed. The expression for the total potential energy can then be written, and minimized, to replace the equilibrium equation. The solution is improved by taking more terms for w.
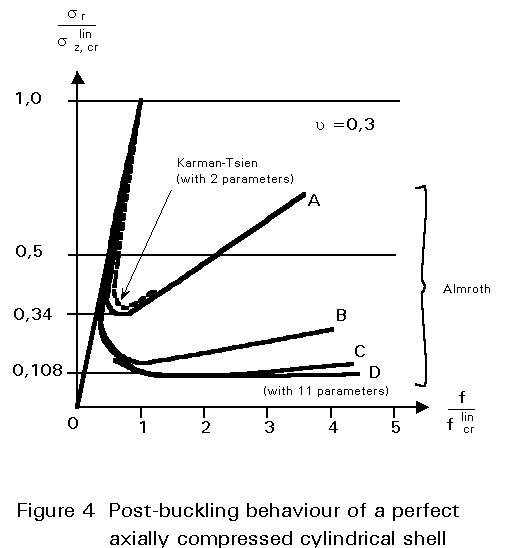
In Figure 4, the results obtained by using only two buckling modes are shown and compared with the curves obtained later, i.e. with a greater number of modes. The results show that the type of curve does not change by increasing the number of modes, but the lowest point of the post-buckling path decreases and can attain a value of about 10% of the linear buckling load. In the limiting case, i.e. where the number of terms increases to infinity, the lowest value of the post-buckling path tends to zero, while the buckling shape tends to assume the shape of the Yoshimura pattern (Figure 5). It is the limiting case of the diamond buckling shape that can be described by the following combination of axi-symmetric and chessboard modes.
![]() (3)
(3)

It is worth noting that the buckling load associated with either the combination or the two single modes is the same and is given by Equation (2).
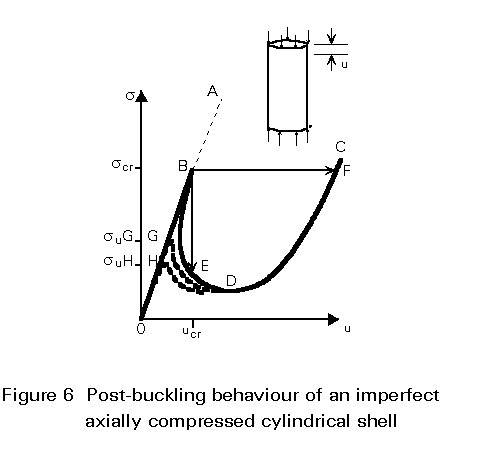
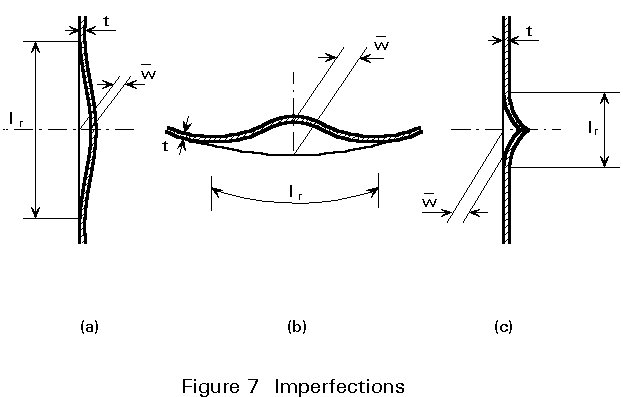
A comprehensive overview of post-buckling theory is given in [5]. As will be discussed later, a realistic theory for shell buckling has to take into account the unavoidable imperfections that appear in real structures. Figure 6 shows the influence of imperfections on the strength of a cylinder subject to compressive loading and Figure 7 shows typical imperfections.
Simple types of shells and loading are amenable to treatment by analytical methods. The buckling load of complex shell structures can, however, be assessed only be means of computer programs, many of which use finite elements and have a stability option. CASTEM, STAGS, NASTRAN, ADINA, NISA, FINELG, ABAQUS, ANSYS, BOSOR and FO4BO8 are some of the general and special purpose programs available. Correct use of a complicated program requires the analyst to be well acquainted with the basis of the approach adopted in the program.
The stability options and the reliability of the numerical results depend on the method of analysis underlying each specific program, and on the buckling modes considered. Analysis of various types may be performed:
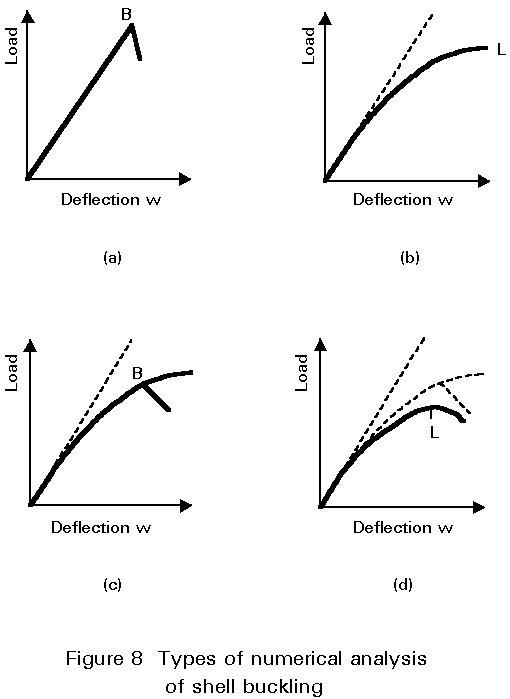
The four load-deflection diagrams given in Figure 8 may relate, for example, to a spherical cap subjected to uniform radial pressure acting towards the centre of the sphere; in this case the critical failure mode depends on the degree of shallowness of the cap.
Equilibrium paths, for a perfectly straight column, a perfectly flat plate supported along its four edges, and a perfectly cylindrical shell, presented in the preceding Lecture 8.6, are repeated here (Figure 9) for completeness.
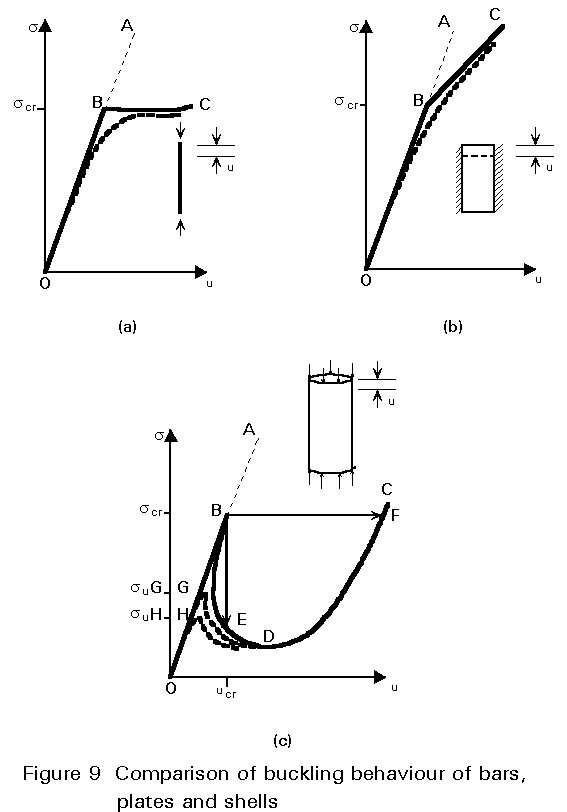
In each diagram, s represents the uniformly applied compressive stress, scr its critical value given by classical stability theory, and U the decrease in distance between the ends of the members.
Each point on the solid or dashed lines represents an equilibrium configuration which is at least theoretically possible, in the sense that the conditions for equilibrium between external and internal forces are met.
Simple elastic shortening, according to Hooke's law, is reflected by the three straight lines OA. They represent the pre-buckling, primary, or fundamental state of equilibrium, in which the column, the plate and the shell remain perfectly straight, flat and cylindrical, respectively.
As long as s < scr, the primary equilibrium is stable, i.e. if a minute accidental disturbance (a very small lateral force, for example) causes a slight transverse deformation of the member, the deformation disappears when its cause is removed, and the member returns of its own accord to its previous configuration. Any point of the line OA, which is located above B, represents, however, unstable equilibrium, i.e. the effect of a disturbance, even an infinitely small one, does not disappear with its cause, but instantaneously increases and the member is set in (violent) motion, deviating further and irreversibly from its previous equilibrium configuration. Some minor cause of disturbance always exists, for example, in the form of an initial shape imperfection or of an eccentricity of loading. A state of unstable equilibrium, therefore, although theoretically possible, cannot occur in real structures.
When the stress reaches its critical value, scr, a new equilibrium configuration appears at point B. This configuration is quite different from the primary one and features lateral deflections and bending of the strut, the plate, or the wall of the shell.
If the new configuration is characterised by displacements with respect to the primary state of equilibrium which increase gradually from zero to high (theoretically infinite) values, the post-buckling states of equilibrium are represented by points on a secondary equilibrium path which intersects with the primary path at the bifurcation point B.
In fact, B is the lowest of an infinite number of bifurcation points, but the paths branching off from all the others represent highly unstable equilibrium and have no practical significance.
The great difference between the strut, the plate and the cylinder is embodied in their post-buckling behaviour. In the case of the column (Figure 9a), the secondary path, BC, is very nearly horizontal, but in reality it curves imperceptibly upwards; the equilibrium along BC is almost neutral (it is, strictly speaking, weakly stable). For the plate (Figure 9b) the secondary path, BC, climbs above B, although less steeply than before; the plate deflects laterally, more and more under a gradually increasing load, but the equilibrium at points on BC is stable.
After bifurcation, the point representing the state of equilibrium of an axially loaded cylinder (Figure 9c), in theory, can travel along the secondary path BDC. The equilibrium at points located below B on the solid curve is, however, highly unstable and, hence, cannot really exist. What would happen after point B is reached, if it were possible to manufacture a perfect cylinder from material of unlimited linear elasticity and to support and load or deform it in the theoretically correct manner, depends on the loading method.
When displacements, u, of one plate of a supposedly rigid testing machine with respect to the other plate are imposed in a controlled manner, buckles suddenly appear in the wall of the cylinder. The compressive stress drops at once from scr to the ordinate of point E (only a fraction of scr), while the shortening of the cylinder remains equal to ucr, the abscissa of B. In contrast with bifurcation, finite displacements are involved in the transition between the equilibrium configurations represented by points B and E; such an occurrence is called snap-through. The buckling process is further complicated by the existence of different intersecting equilibrium paths, which correspond to different numbers of circumferential buckling waves and which have the same general shape as BDC. Some parts of these paths represent stable equilibrium, while other parts represent unstable equilibrium; after the initial snap-through from state B to state E, the shell can jump repeatedly from one buckling configuration to another.
When the load, rather than the displacement, u, is controlled a different effect occurs; if, for example, a load = 2prtscr is imposed, the overall shortening of the cylinder almost instantly increases from ucr to the abscissa of point F, and its wall suddenly exhibits deep buckles, while the average compressive stress remains equal to scr. It should be noted that this "snap-through" has dynamic characteristics which are not considered in this description.
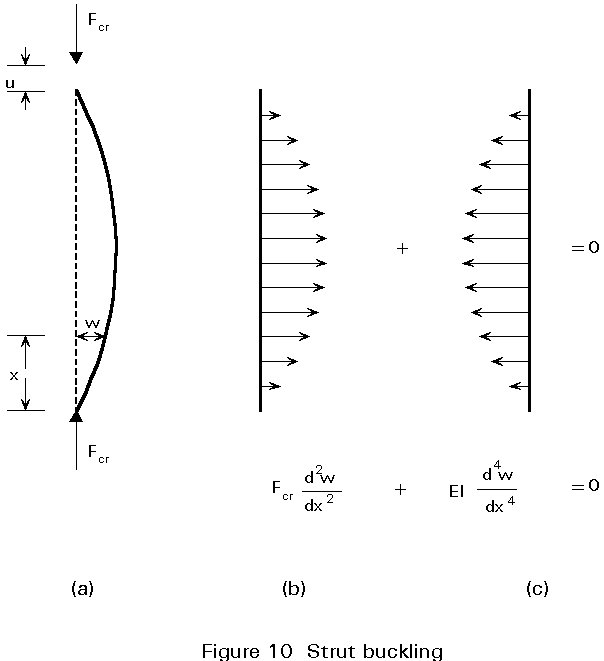
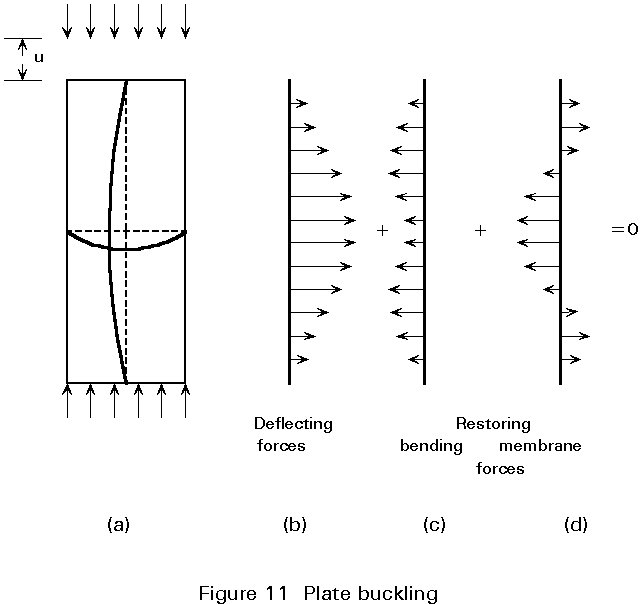
Esslinger and Geier [5] explain the fundamentally different behaviour of columns, plates and shells by the following argument illustrated by Figures 10, 11 and 12.

The differential equation
![]()
expresses the lateral equilibrium of any element of an axially loaded strut when bifurcation occurs (Figure 10a) by stating that the deflecting force per unit length, due to the external loads, Fcr, given by the first term, cancels out the restoring force per unit length, due to the internal bending stresses, given by the second term. Both the deflecting forces (Figure 10b) and the restoring forces (Figure 10c) are proportional to the lateral deflection. Consequently, equilibrium of the column is independent of the magnitude of the transverse deformation and of u, for a given constant axial force Fcr.
The restoring forces which balance the lateral forces (Figure 11b) deflecting a buckling plate (Figure 11a), are due not only to longitudinal and transverse bending moments (Figure 11c), but also to transverse membrane forces (Figure 11d). The restoring forces due to membrane action are zero, as long as the plate is flat, but they then increase proportionately to the square of its lateral deflection. As a result, the compressive external load required for equilibrium increases together with the lateral deformation and with the plate shortening u.
Figure 12a shows the radial component of the buckling pattern of a compressed cylinder at the bifurcation point. Outward displacements of a curved surface cause tensile membrane forces, while inward displacements generate compressive membrane forces. Figure 12b gives a more accurate picture of an inward buckle of very small amplitude; it is seen that the original sign of the circumferential curvature of the shell wall is not reversed at the start of buckling. The radial forces arising from the combination of the membrane forces with the curvature of the deformed cylinder, which still has its initial sign, are shown in Figure 12c. These radial forces all tend to counteract buckling. Hence the high resistance of a perfect cylinder to the initiation of buckling, given by Equation (2). Increasing inward displacements cause the change of circumferential curvature to exceed the magnitude, 1/r, of the original curvature of the cylinder, as shown in an exaggerated manner in Figure 12d, and more realistically in Figure 12e. In the region of the inward buckles, the wall of the cylinder is now curved inwards and, as a result, the compressive membrane forces in these areas no longer resist the appearance of dents, but precipitate them (Figure 12f). Hence, the total restoring effect of the membrane forces has now weakened substantially compared with the state prevailing at the bifurcation point. The upshot is that, once buckling has started, equilibrium is conceivable only under decreasing axial load.
The behaviour of actual imperfect components differs from the theoretical behaviour described above and is represented by the dotted curves in Figure 9. They show that true bifurcation of equilibrium does not actually occur in the case of real structural members. However, the solid lines provide an approximate picture - the smaller the initial imperfections, the truer the picture is - of the behaviour of the component, and therein lies the significance of the bifurcation buckling concept.
The dotted lines in Figures 9a and 9b, have been drawn for a column and a plate with slight initial curvature. It can be seen that the carrying resistance of the strut is not much lower than the theoretical buckling load, provided that the imperfection is not too great. One can conclude from Figure 9b that the equilibrium path of an imperfect plate may not exhibit any discontinuity when the compressive stress increases beyond scr, and also that the plate may possess a considerable post-buckling strength reserve. If it is thin, this reserve may be considerably greater than the bifurcation buckling load. Raising the stress beyond scr for the perfect plate does not bring about immediate ultimate failure. Both the column and the plate finally fail by yielding caused by excessive bending.
Owing to the imperfection of a real cylinder, the dotted equilibrium path does not display the very sharp high peak B which is a feature of the theoretical equilibrium path OBDC. The culminating point G or H (Figure 9c) of the dotted line, called a limit point, is at a much lower level than the bifurcation point, even when the amplitude of the initial deviations from the perfect cylindrical shape is minute. The lower dotted curve is the equilibrium path for a cylinder with somewhat larger imperfections. When the loading is due to weight and happens to correspond to the limit point, the curve must jump horizontally from G or H towards the right hand branch of the curve. The concomitant shortening, u, of the steel shell is so large, and due to buckles which are so deep, that normally part of the wall material is strained into the plastic range and so the buckling phenomenon, in this case a snap-through or non-linear collapse, is almost always catastrophic.
One should not infer from the description in the preceding paragraph that only imperfect structural components display behaviour characterized by a limit point. Due to gradual changes in the geometry of a perfect structure, its primary equilibrium path may be non-linear from the outset of loading and, indeed, feature a limit point.
As a summary two points can be established:
A sweeping generalization to the effect that all shells are always very sensitive to deviations from the perfect shape would be unwarranted. The imperfection sensitivity depends on the type of shell and loading. It may vary from slight to extreme, even for the same kind of shell under different loading conditions. For example, the imperfection sensitivity of cylindrical shells under uniform external pressure is quite low, whilst the same shells are highly imperfection sensitive when they are compressed in the meridional direction. The difference relates to the buckling mode; under axial load, the buckling modes are characterised by waves which, compared to the diameter, are short in both the longitudinal and the circumferential direction. Small initial imperfections, which may occur anywhere on the surface of the cylinder and which are likely to have roughly the same shape as some of the critical buckles, tend to deepen under increasing load and to trigger off a snap-through at an early loading stage. The buckling pattern under external pressure, however, consists of buckles which are long in the meridional direction, and less numerous in the hoop direction, and therefore probably of considerably larger size than the principal initial dents and bulges.
Another factor that should be mentioned as contributing to the imperfection sensitivity of axially loaded cylinders is the multiplicity of different buckling modes associated with the same bifurcation load. Any realistic theoretical treatment of the buckling problem is complicated further by the existence of residual stresses due to cold or hot forming and/or due to welding. Behaviour is also affected by the appearance of plastic deformations in the steel and, in some cases, by the presence of stiffeners. The non-linear structural behaviour of the shell may be due to the latter, as well as to changes in the geometry resulting from the deformation of the shell.
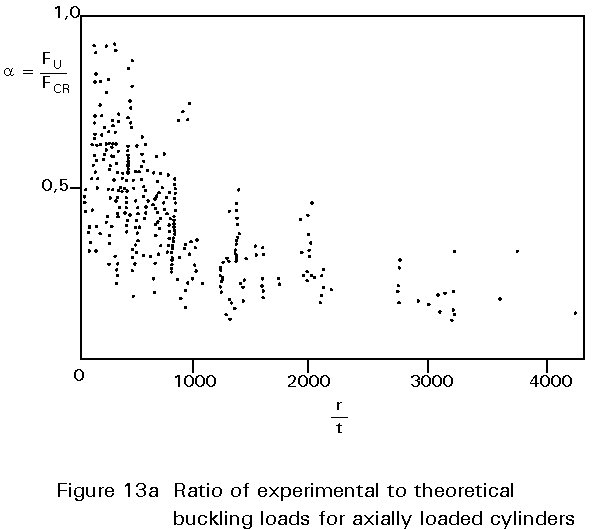
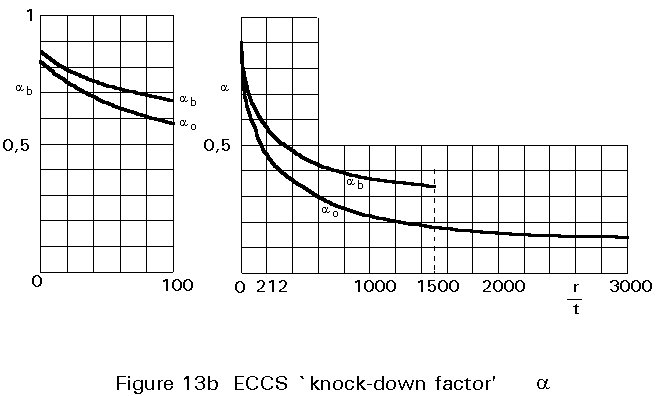
In conclusion, imperfections are the main cause of the large difference between the ultimate load obtained in tests and the theoretical buckling load. A wide scatter of results for nominally identical shells can be seen in Figure 13a where the ratio of experimental buckling loads, Fu, against the theoretical values, Fcr, for axially loaded cylinders are given for different r/t ratios. Figure 13b gives the factors proposed by ECCS to reduce the theoretical buckling load to values appropriate for design.
[1] Timoshenko, S. and Woinowsky-Krieger, S., "Theory of Plates and Shells", McGraw-Hill, New York and Kogakusha, Tokyo, 1959.
[2] Flügge, W., "Stresses in Shells", Springer-Verlag, New York, 1967.
[3] Bushnell, D., "Computerised Buckling Analysis of Shells", Martinus Nijhoff Publishers, Dordrecht, 1985.
[4] Timoshenko, S. and Gere, J.M., "Theory of Elastic Stability", McGraw-Hill, New York and Kogakusha, Tokyo, 1961.
[5] Esslinger, M. T., and Geier, B. M., "Buckling and Post Buckling Behaviour of Thin-Walled Circular Cylinders", International Colloquium on Progress of Shell Structures in the last 10 years and its future development, Madrid, 1969.