
ESDEP WG 7
ELEMENTS
To describe the different kinds of steel columns and to explain the procedures involved in the design of compression members.
Lecture 6.1: Concepts of Stable and Unstable Elastic Equilibrium
Lecture 7.2: Cross-Section Classification
Lecture 7.3: Local Buckling
Lecture 7.6: Built-up Columns
Lectures 7.10: Beam Columns
Lecture 7.12: Trusses and Lattice Girders
Worked Example 7.5: Column Design
Different kinds of compression members (uniform and non-uniform cross-sections and built-up columns) are described. The differences between stocky and slender columns are explained and the basis for design, using the European buckling curves, is outlined.
Columns are vertical members used to carry axial compression loads. Such structural elements are found, for example, in buildings supporting floors, roofs or cranes. If they are subjected to significant bending moments in addition to the axial loads, they are called beam-columns.
The term 'compression' member is generally used to describe structural components subjected only to axial compression loads; this can describe columns (under special loading conditions) but generally refers to compressed pin-ended struts found in trusses, lattice girders or bracing members.
This lecture deals with compression members and, therefore, concerns very few real columns because eccentricities of the axial loads and, above all, transverse forces, are generally not negligible. Nevertheless, compression members represent an elementary case which leads to the understanding of the term of compression in the study of beam-columns (Lectures 7.10.1 and 7.10.2), frames (Lecture 7.11), and trusses and lattice girders (Lecture 7.12).
Because most steel compression members are rather slender, buckling can occur; this adds an extra bending moment to the axial load and must be carefully checked.
The lecture briefly describes the different kinds of compression members and explains the behaviour of both stocky and slender columns; the buckling curves used to design slender columns are also given.
For optimum performance compression members need to have a high radius of gyration, i, in the direction where buckling can occur; circular hollow sections should, therefore, be most suitable in this respect as they maximise this parameter in all directions. The connections to these sections are, however, expensive and difficult to design.
It is also possible to use square or rectangular hollow sections whose geometrical properties are good (the square hollow sections being the better); the connections are easier to design than those of the previous shape, but again rather expensive.
Hot-rolled sections are, in fact, the most common cross-sections used for compression members. Most of them have large flanges designed to be suitable for compression loads. Their general square shape gives a relatively high transverse radius of gyration iz and the thickness of their flanges avoids the effect of local buckling (care has to be taken in the case of light H-sections and high strength steel). The open shape, produced by traditional rolling techniques, facilitates beam-to-column and other connections.
Welded box or welded H-sections are suitable if care is taken to avoid local flange buckling. They can be designed for the required load and are easy to connect to other members; it is also possible to reinforce these shapes with welded cover plates.
Figure 1 illustrates all the shapes mentioned above.

It should be noted that:
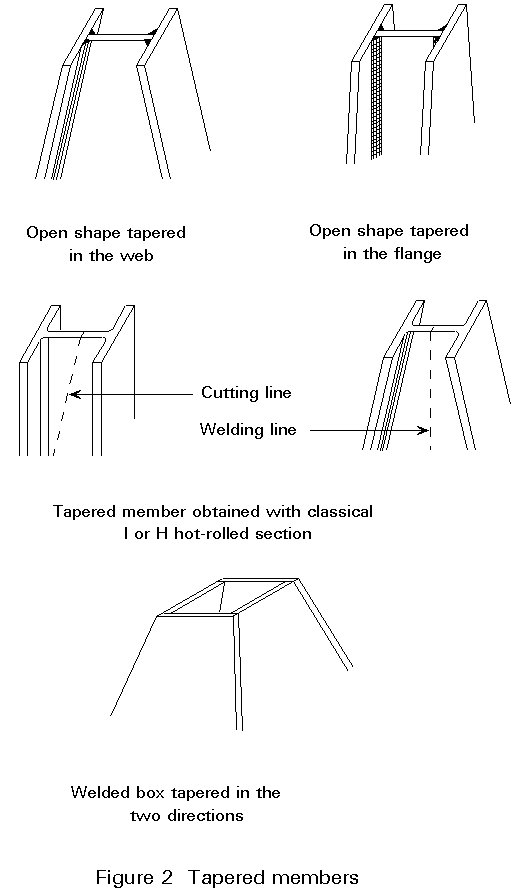
Members with changes of cross-section within their length, are called non-uniform members; tapered and stepped members are considered in this category.
In tapered members (Figure 2) the cross-section geometry changes continuously along the length; these can be either open or box shapes formed by welding together elements, including tapered webs, or flanges, or both. A classical example is that of a hot-rolled H or I-section whose web is cut along its diagonal; a tapered member is obtained by reversing and welding the two halves together.
Stepped columns (Figures 3) vary the cross-section in steps. A typical example of their use is in industrial buildings with overhead travelling cranes; the reduced cross section is adequate to support the roof structure but must be increased at crane level to cater for the additional loads. Stepped columns can also be used in multi-storey buildings to resist the loads in the columns at the lower levels.

Built-up columns are fabricated from various different elements; they consist of two or more main components, connected together at intervals to form a single compound member (Figure 4). Channel sections and angles are often used as the main components but it is also possible to use I or H-sections; they are laced or battened together with simple elements (bars or angles or smaller channel sections) and it is possible to find columns where both methods are combined (Figure 5). Columns with perforated plates (Figure 6) are also considered in this category.
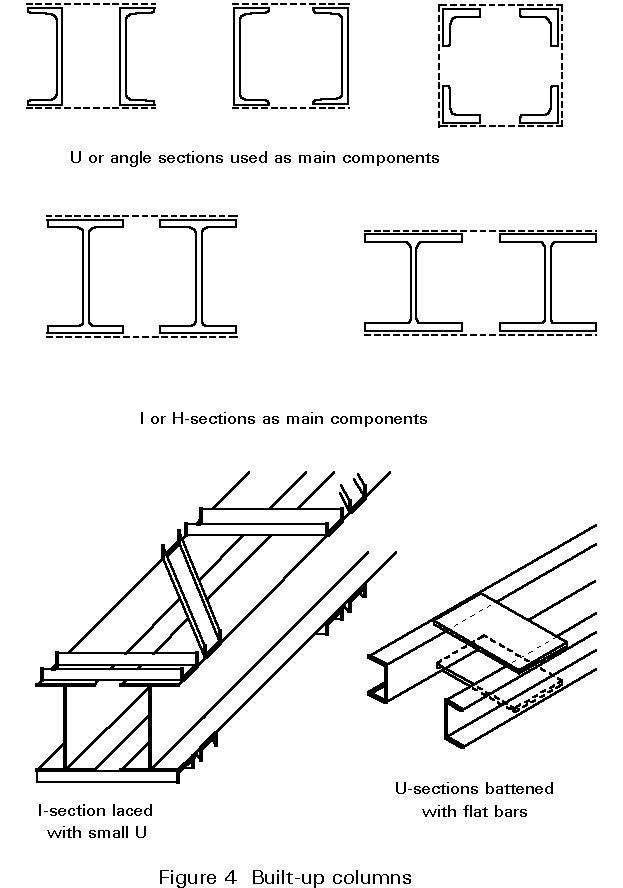
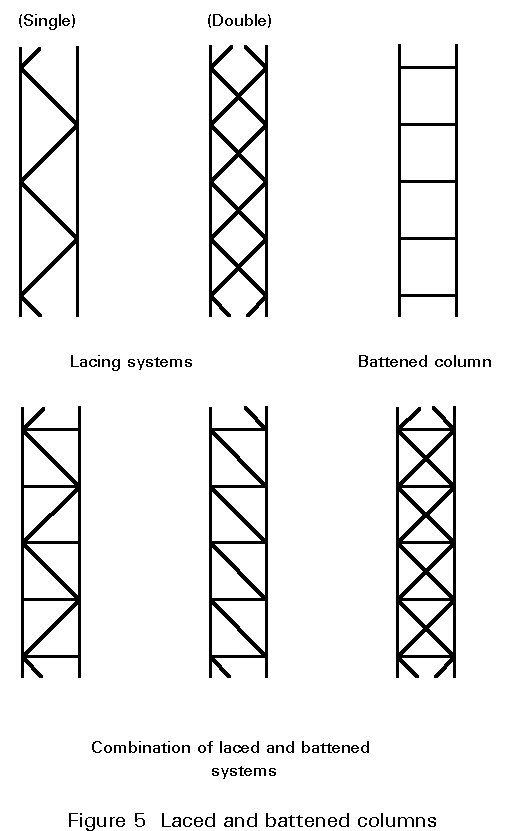
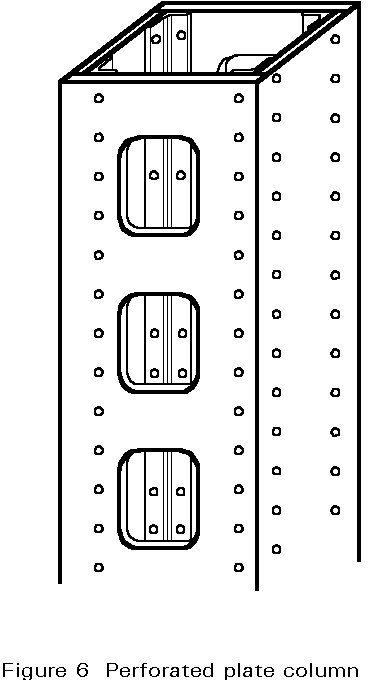
The advantage of this system is that it gives relatively light members which, because most of the steel is placed quite far from the centre of gravity of the cross-section have a relatively high radius of gyration. The most important disadvantage comes from the high fabrication costs involved. These members are generally designed for large structures where the compression members are long and subjected to heavy loads. It is to be noted that buckling of each individual element must be checked very carefully.
Figure 7 shows some closely spaced built-up members and gives details of star-battened angle members. These are not so efficient as the previous ones because of their smaller radius of gyration; however, the ease with which these can be connected to other members may make their use desirable. They behave in compression in a similar way to those described above, hence their inclusion in this section.

Built-up columns may have uniform or non-uniform cross-sections; it is possible, for example, to find stepped or tapered built-up columns (Figure 8).
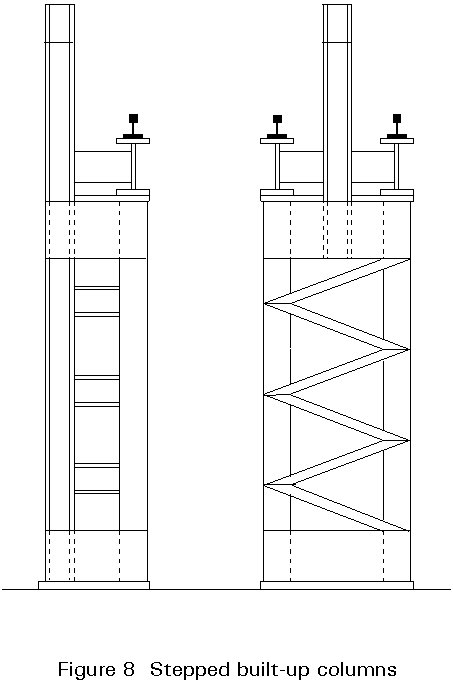
The design of built-up columns will be examined in Lecture 7.6.
Stub (or stocky) columns are characterised by very low slenderness, are not effected by buckling and can be designed to the yield stress fy.
If local buckling does not affect the compression resistance (as can be assumed for Class 1, 2 and 3 cross-sections), the mode of failure of such members corresponds to perfect plastic behaviour of the whole cross-section, which theoretically occurs when each fibre of the cross-section reaches fy. It is to be noted that residual stresses and geometric imperfections are practically without influence on the ultimate strength of this kind of column and that most experimental stub columns fail above the yield stress because of strain-hardening.
The maximum compression resistance Nmax is, therefore, equal to the plastic resistance of the cross-section:
Nmax = Npl = Aeff fy (1)
Aeff is the effective area of the cross-section, see Section 3.2.
Eurocode 3 [1] considers that columns are stocky when their reference slenderness ![]() is such that
is such that ![]() £ 0,2 (
£ 0,2 (![]() is defined in Section 5.1). They are represented by a plateau on the ECCS curves [2], see Section 5.2.
is defined in Section 5.1). They are represented by a plateau on the ECCS curves [2], see Section 5.2.
The effective area of the cross-section used for design of compression members with Class 1, 2 or 3 cross-sections, is calculated on the basis of the gross cross-section using the specified dimensions. Holes, if they are used with fasteners in connections, need not be deducted.
Depending on their slenderness, columns exhibit two different types of behaviour: those with high slenderness present a quasi elastic buckling behaviour whereas those of medium slenderness are very sensitive to the effects of imperfections.
If lcr is the critical length, the Euler critical load Ncr is equal to:
Ncr = ![]() (2)
(2)
and it is possible to define the Euler critical stress scr as:
s
cr =By introducing the radius of gyration, i = ![]() , and the slenderness, l = lcr/i, for the relevant buckling mode, Equation (3) becomes:
, and the slenderness, l = lcr/i, for the relevant buckling mode, Equation (3) becomes:
s
cr =Plotting the curve scr as a function of l on a graph (Figure 9), with the line representing perfect plasticity, s = fy, shown, it is interesting to note the idealised zones representing failure by buckling, failure by yielding and safety.
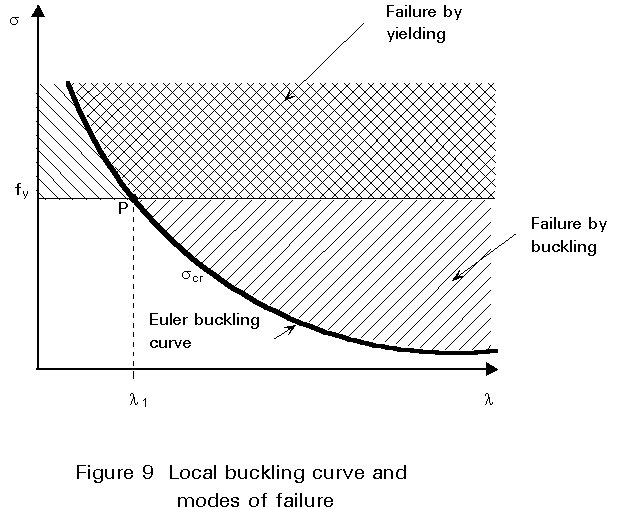
The intersection point P, of the two curves represents the maximum theoretical value of slenderness of a column compressed to the yield strength. This maximum slenderness (sometimes called Euler slenderness), called l1 in Eurocode 3, is equal to:
l
1 = P [E/fy]1/2 = 93,9e (5)where: e = [235/fy]1/2 (6)
l
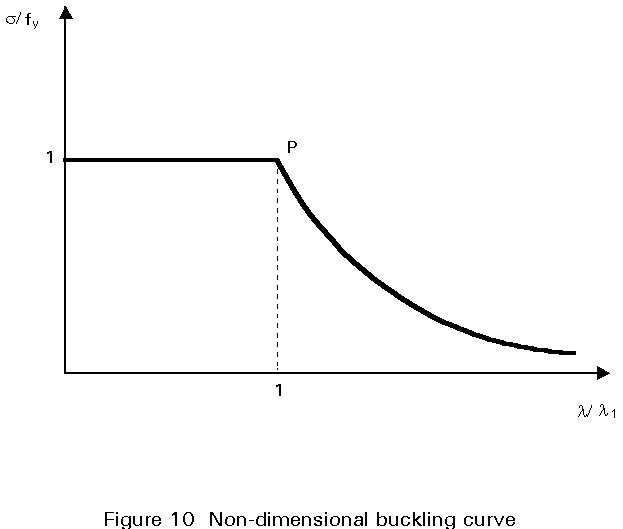
1 is equal to 93,9 for steel grade Fe 235 and to 76,4 for steel grade Fe 355.A non-dimensional representation of this diagram is obtained by plotting s/fy as a function of l/l 1 (Figure 10); this is the form used for the ECCS curves (see Section5.2). The coordinates of the point P are, therefore, (1,1).
The real behaviour of steel columns is rather different from that described in the previous section and columns generally fail by inelastic buckling before reaching the Euler buckling load. The difference in real and theoretical behaviour is due to various imperfections in the "real" element: initial out-of-straightness, residual stresses, eccentricity of axial applied loads and strain-hardening. The imperfections all affect buckling and will, therefore, all influence the ultimate strength of the column. Experimental studies of real columns give results as shown in Figure 11. Compared to the theoretical curves, the real behaviour shows greater differences in the range of medium slenderness than in the range of large slenderness. In the zone of the medium values of l (representing most practical columns), the effect of structural imperfections is significant and must be carefully considered. The greatest reduction in the theoretical value is in the region of Euler slenderness l1. The lower bound curve is obtained from a statistical analysis and represents the safe limit for loading.

a. Slender columns
A column can be considered slender if its slenderness is larger than that corresponding to the point of inflexion of the lower bound curve, shown in Figure 11.
The ultimate failure load for slender columns is close to the Euler critical load Ncr. As this is independent of the yield stress, slender columns are often designed using the ratio: l2 = (A lcr2)/I, a geometrical characteristic independent of the mechanical strength.
Individual or star-battened angles or small flat plates have generally a poor second moment of area about the minor axis, relative to their cross-section area. This can result in large slenderness with high sensitivity to buckling and explains why classical cross-bracing systems, using these shapes, are only designed in tension.
b. Columns of medium slenderness
Columns of medium slenderness are those whose behaviour deviates most from Euler's theory. When buckling occurs, some fibres have already reached the yield strength and the ultimate load is not simply a function of slenderness; the more numerous the imperfections, the larger the difference between the actual and theoretical behaviour. Out-of-straightness and residual stresses are the imperfections which have the most significant effect on the behaviour of this kind of column.
Residual stresses can be distributed in various ways across the section. They are produced by welding, hot-rolling, flame-cutting or cold-forming; Figure 12a shows some of the stress patterns that can occur.

Residual stresses combined with axial stresses are shown in Figure 12b. If the maximum stress sn reaches the yield stress fy, yielding begins to occur in the cross-section. The effective area able to resist the axial load is, therefore, reduced.
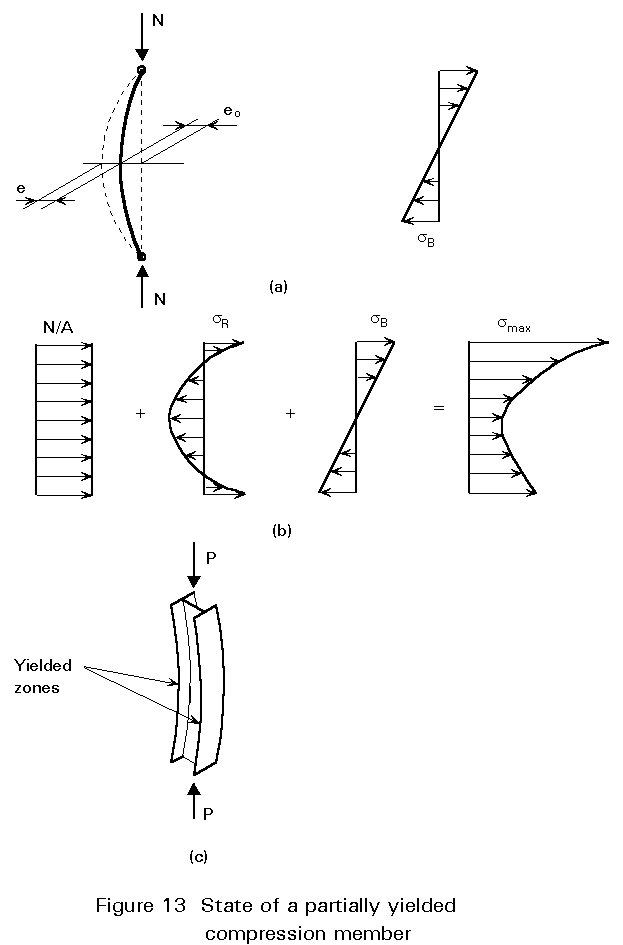
Alternatively, an initial out-of-straightness eo, produces a bending moment giving a maximum bending stress sB (see Figure 13a), which when added to the residual stress, sR gives the stress distribution shown in Figure 13b. If smax is greater than the yield stress the final distribution will be part plastic and part of the member will have yielded in compression, as shown in Figure 13c.
The reference slenderness ![]() is defined as the following non-dimensional parameter for Class 1, 2 or 3 cross-sections:
is defined as the following non-dimensional parameter for Class 1, 2 or 3 cross-sections:
![]() = l /l1
(7)
= l /l1
(7)
where l and l1 are defined in Section 4.1.
![]() can also be written in the following form:
can also be written in the following form:
![]() 2
= l2fy/p2E =
fy/scr
(8)
2
= l2fy/p2E =
fy/scr
(8)
or ![]() =
= ![]() (9)
(9)
From 1960 onwards, an international experimental programme was carried out by the ECCS to study the behaviour of standard columns [2]. More than 1000 buckling tests, on various types of members (I, H, T, U, circular and square hollow sections), with different values of slenderness (between 55 and 160) were studied. A probabilistic approach, using the experimental strength, associated with a theoretical analysis, showed that it was possible to draw some curves describing column strength as a function of the reference slenderness. The imperfections which have been taken into account are: a half sine-wave geometric imperfection of magnitude equal to 1/1000 of the length of the column; and the effect of residual stresses relative to each kind of cross-section.
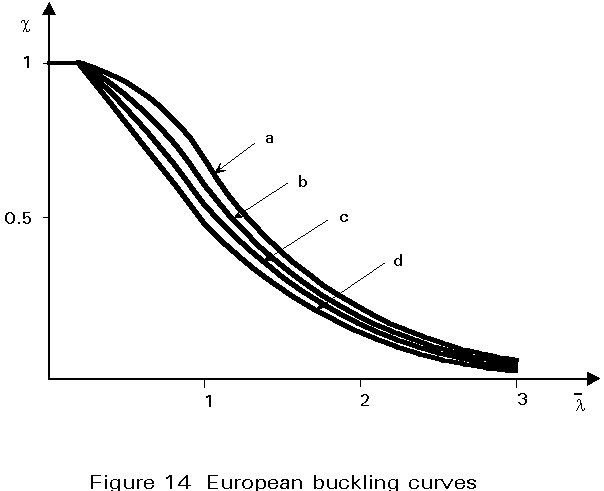
The European buckling curves (a, b, c or d) are shown in Figure 14. These give the value for the reduction factor c of the resistance of the column as a function of the reference slenderness for different kinds of cross-sections (referred to different values of the imperfection factor a).
The mathematical expression for c is:
c
= 1/ {f + [f2 -where: f = 0,5 [1 + a (![]() - 0,2) +
- 0,2) +
![]() 2]
(11)
2]
(11)
Table 1 gives values of the reduction factor c as a function of the reference slenderness ![]() .
.
The imperfection factor a depends on the shape of the column cross-section considered, the direction in which buckling can occur (y axis or z axis) and the fabrication process used on the compression member (hot-rolled, welded or cold-formed); values for a, which increase with the imperfections, are given in Table 2.
Curve a represents quasi perfect shapes: hot-rolled I-sections (h/b > 1,2) with thin flanges (tf £ 40mm) if buckling is perpendicular to the major axis; it also represents hot-rolled hollow sections.
Curve b represents shapes with medium imperfections: it defines the behaviour of most welded box-sections; of hot-rolled I-sections buckling about the minor axis; of welded I-sections with thin flanges (tf £ 40mm) and of the rolled I-sections with medium flanges (40 < tf £ 100mm) if buckling is about the major axis; it also concerns cold-formed hollow sections where the average strength of the member after forming is used.
Curve c represents shapes with a lot of imperfections: U, L, and T shaped sections are in this category as are thick welded box-sections; cold-formed hollow sections designed to the yield strength of the original sheet; hot-rolled H-sections (h/b £ 1,2 and tf £ 100mm) buckling about the minor axis; and some welded I-sections (tf £ 40mm buckling about the minor axis and tf > 40mm buckling about the major axis).
Curve d represents shapes with maximum imperfections: it is to be used for hot-rolled I-sections with very thick flanges (tf > 100mm) and thick welded I-sections (tf > 40mm), if buckling occurs in the minor axis.
Table 4 helps the selection of the appropriate buckling curve as a function of the type of cross-section, of its dimensional limits and of the axis about which buckling can occur. For cold-formed hollow sections, fyb is the tensile yield strength and fya is the average yield strength. If the cross-section in question is not one of those described, it must be classified analogously.
It is important to note that the buckling curves are established for a pin-ended, end loaded member; it is necessary carefully to evaluate the buckling lengths if the boundary conditions are different, see Lecture 7.7.
To study a column using second order theory, it is necessary to choose geometrical imperfections (initial out-of-straightness and eccentricities of loading) and mechanical imperfections (residual stresses and variations of the yield stress). Eurocode 3 proposes values for a bow imperfection, eo, whose effect is equivalent to a combination of the two previous kinds of imperfections [1].
If the column is designed using elastic analysis, eo is as follows:
eo = a (![]() - 0,2) Wpl/A for plastic design of cross-sections
- 0,2) Wpl/A for plastic design of cross-sections
or,
eo = a (![]() - 0,2) Wel/A
for elastic design of cross-sections
(12)
- 0,2) Wel/A
for elastic design of cross-sections
(12)
If it is designed with an elastic-plastic analysis (elasto-plastic or elastic-perfectly plastic), the values of eo are functions of the buckling length L, and are given in Table 3.
To design a simple compression member it is first necessary to evaluate its two effective lengths, in relation to the two principal axes, bearing in mind the expected connections at its ends. Secondly, the required second moment of area to resist the Euler critical loads should be calculated to give an idea of the minimum cross-section necessary. The verification procedure should then proceed as follows:
Buckling resistance of a compression member is then taken as:
Nb.Rd = c A fy/gM1 (13)
the plastic resistance as:
Npl.Rd = A fy/gM0 (14)
and the local buckling resistance as:
No.Rd = Aeff fy/gM1 (15)
If these are higher than the design axial load, the column is acceptable; if not, another larger cross-section must be chosen and checked.
In addition, torsional or flexural-torsional buckling of the column must be prevented.
[1] Eurocode 3: " Design of Steel Structures": ENV 1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.
Table 1 Reduction factors
|
|
Reduction factor c |
|||
|
Curve a |
Curve b |
Curve c |
Curve d |
|
|
0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 |
1,0000 0,9775 0,9528 0,9243 0,8900 0,8477 0,7957 0,7339 0,6656 0,5960 0,5300 0,4703 0,4179 0,3724 0,3332 0,2994 0,2702 0,2449 0,2229 0,2036 0,1867 0,1717 0,1585 0,1467 0,1362 0,1267 0,1182 0,1105 0,1036 |
1,0000 0,9641 0,9261 0,8842 0,8371 0,7837 0,7245 0,6612 0,5970 0,5352 0,4781 0,4269 0,3817 0,3422 0,3079 0,2781 0,2521 0,2294 0,2095 0,1920 0,1765 0,1628 0,1506 0,1397 0,1299 0,1211 0,1132 0,1060 0,0994 |
1,0000 0,9491 0,8973 0,8430 0,7854 0,7247 0,6622 0,5998 0,5399 0,4842 0,4338 0,3888 0,3492 0,3145 0,2842 0,2577 0,2345 0,2141 0,1962 0,1803 0,1662 0,1537 0,1425 0,1325 0,1234 0,1153 0,1079 0,1012 0,0951 |
1,0000 0,9235 0,8504 0,7793 0,7100 0,6431 0,5797 0,5208 0,4671 0,4189 0,3762 0,3385 0,3055 0,2766 0,2512 0,2289 0,2093 0,1920 0,1766 0,1630 0,1508 0,1399 0,1302 0,1214 0,1134 0,1062 0,0997 0,0937 0,0882 |
Table 2 Imperfection factors
|
Buckling curve |
a |
b |
c |
d |
|
Imperfection factor a |
0,21 |
0,34 |
0,49 |
0,76 |
Table 3 Equivalent initial bow imperfections
|
Buckling curve |
Elasto-plastic |
Elastic-perfectly plastic |
|
a b c d |
L/600 L/380 L/270 L/180 |
L/400 L/250 L/200 L/150 |
Table 4: Selection of buckling curve for a cross-section
