ESDEP WG 6
APPLIED STABILITY
To present and illustrate the application of methods which can be used to solve stability problems iteratively.
None.
Lecture 6.1: Concepts of Stable and Unstable Elastic Equilibrium
Lecture 6.2: General Criteria for Elastic Stability
Lecture 6.3: Elastic Instability Modes
Lecture 6.4: General Methods for Assessing Critical Loads
Worked Example 6.3: Application of Vianello's/Newmark's/Vianello-Newmark Methods
This lecture begins with an introduction which describes the reasons for using iterative methods to solve stability problems. Then the Vianello Method is introduced. Next, the method of Newmark for the calculation of internal forces and deflections in transversally loaded beams is reviewed as a preliminary step to the presentation of the Vianello-Newmark method. This method combines Vianello's method with Newmark's integration procedure.
Even when deflections are assumed to be small, stability problems are always non-linear, in the sense that the equilibrium equations and boundary conditions must be established for the deformed configuration of the structure. As a result, only in very simple cases, is it possible to obtain analytical solutions of the eigenvalue-eigenfunction problem, leading to the determination of the critical buckling load and corresponding instability mode (see Lecture 6.3). In general it is necessary to resort to approximate methods. One very important group of such methods - energy methods - was presented in Lecture 6.4. Basically, these methods consist of replacing the original continuous structure by a simpler discrete structure. This was achieved by constraining the real structure to deform in a manner which is the superposition of a set of defined shapes with unspecified amplitudes. The exact critical buckling load and mode of this simpler structure, which is the solution of an eigenvalue-eigenvector problem similar to the one addressed in Lecture 6.2, are approximate solutions for the original structure. Although the accuracy of these methods (and the effort involved) increases with the number of degrees of freedom considered, very satisfactory approximations can often be obtained using only a small number. One major drawback of energy methods is that they always lead to upper bounds of the critical buckling load, which is not convenient in design. The discretization procedure of a continuous structure may also be achieved by dividing it into several rigid elements connected by springs that provide its stiffness. The deformation of the structure is a piecewise continuous function which is completely defined by the displacements of the nodes connecting the elements. The exact solution of this discretised structure was addressed in Lecture 6.2 and is also an approximate solution of the original problem. However, in this case nothing can be said concerning the amount or sign of the error. As before the accuracy also increases with the number of elements.
Thus the determination of the critical buckling load and mode of a structure requires the solution of a non-linear problem which is either a linear eigenvalue-eigenvector problem (discrete or discretised systems) or, a linear eigenvalue-eigenfunction problem (continuous systems). In the first case an analytical solution is always possible but it requires the determination of the lowest root of the characteristic equation, which is often of a relatively high degree. In the second case an analytical solution is possible only for simple problems. An alternative to either of these problems is provided by an iterative method first introduced by Vianello and, therefore, designated as Vianello's method. The basic idea consists of replacing the solution of the non-linear problem by the solution of a sequence of linear problems which can be shown to converge to the critical buckling mode and enable the calculation of the critical buckling load. A feature of Vianello's method which is very convenient in the design and safety checking of structures, is that it is possible, after each iteration, to calculate upper and lower bounds of the critical buckling load and, therefore, to estimate the corresponding error.
Finally, the Vianello-Newmark method combines the concept of Vianello's method with Newmark's numerical integration technique. It is a very efficient alternative for the determination of critical buckling loads and modes of axially loaded columns, particularly if some non-standard features are present in the loads, the column or its supporting conditions. This method can also be used to determine equilibrium configurations of columns acted on by specified axial loads and containing initial geometrical imperfections or transverse loads, i.e.beam-columns.
Vianello's method is an iterative procedure which may be used to determine approximately the critical buckling load and mode of continuous or discrete structural systems acted on by a set of loads that may be expressed in terms of a single load parameter l (proportional loading). The method is based directly on the differential equation (system of simultaneous equations) of equilibrium of the system, which means that it does not involve energy concepts. The application of the method consists of the following steps:
(i) Make an initial estimate of the deflected configuration associated with the critical buckling mode of the structure, which must satisfy the kinematic boundary conditions. This initial estimate is a vector (discrete systems) or a function (continuous systems).
(ii) Based upon this assumed configuration calculate the internal forces in terms of the unknown buckling loading parameter l. These internal forces are concentrated forces and/or moments (discrete systems) or bending moments (continuous systems).
(iii) Using a standard linear analysis determine the deflected configuration produced by the internal forces calculated in (ii). This new deflected configuration, which depends on l, constitutes an improved approximation of the critical buckling mode of the structure. The linear analysis involves the solution of a system of simultaneous equilibrium equations (discrete or discretized systems) or of a differential equation (continuous systems).
(iv) Equate the assumed and calculated deflections mentioned in (i) and (iii) to obtain upper and lower bounds and an estimate of the critical value of the load parameter lcr. In discrete systems the upper (lower) bound of lcr is the larger (small) value of l required to equalize a pair of corresponding non-zero components of the vectors defining the assumed and calculated deflections. A possible estimate of l is required to equalize the values of the functions defining the assumed and calculated deflections at a point of non-zero value. These bounds are often rather difficult to calculate and only an estimate of lcr is determined, which is the value of l required to equalize the functions at a specified point.
(v) Repeat the process using as initial estimate the shape of the deflection calculated in the previous iteration. Stop whenever the desired accuracy is achieved. It is often convenient, for numerical reasons, to normalize the calculated deflection before using it as the initial estimate in the next iteration. The accuracy of the solution is measured either by the difference between the upper and lower bounds or by the proximity of the consecutive estimates of lcr.
It can be shown that the process converges to the critical instability mode, therefore allowing the calculation of the critical buckling load parameter lcr.
Mathematically, the essence of Newmark's method is a numerical integration technique for solving differential equations of the type 
= f (x). It leads to a rapid and systematic calculation of shears and moments in arbitrary statically determinate beams acted on by transverse loads. Through the combination of Newmark's integration scheme with the conjugate beam method, it is possible to calculate also slopes and deflections due to bending. Statically indeterminate beams may be analysed by the force method, with Newmark's method providing a straightforward way of determining the flexibility matrix.
The sign conventions are chosen so that quantities may be added when proceeding from left to right across the beam and subtracted in the opposite case. Then, the axial force (N) is positive if it is compressive, the shear force (V) is positive if it tends to turn clockwise, the bending moment (M) and curvature (c) are positive when the top fibres are compressed, the slope (q) is positive upwards to the right, the lateral deflection (y) and applied loads (q, Q) are positive upwards, and the axial applied load (P, p) are positive from left to right.
In order to apply Newmark's method it is necessary to divide the beam into several equal segments. Each division point is referred to as a station. The number of stations must enable a good description of the beam, loads and supporting conditions. When the loading consists of concentrated loads acting at the stations, the method determines the shears in the segments and the moments at the stations exactly. The shears are determined by summing algebraically the loads along the beam and the bending moments are found by adding or subtracting the product of successive shears and the lengths of the segments over which they act. When the value of the shear or moment is not known at any point along the beam, the calculations may be continued on the basis of some arbitrary chosen value (usually zero), with a linear or constant correction added later to the resulting moments (shears).
When the beam is acted on by distributed loads they must be replaced by equivalent concentrated loads acting at the stations. Physically, these loads represent the reactions of a series of hypothetical weightless stringers coinciding with the segments and interposed between the loads and the beam (see Figure 1). The stringer reactions are equivalent to the distributed loads in the sense that they produce the same shears and bending moments at the stations. The formulae for computing the equivalent concentrated loads are exact respectively for linear and parabolic loading distributions, and approximate for higher order distributions. The formulae for end stations must also be used whenever there is a jump in the magnitude or slope of the applied load.
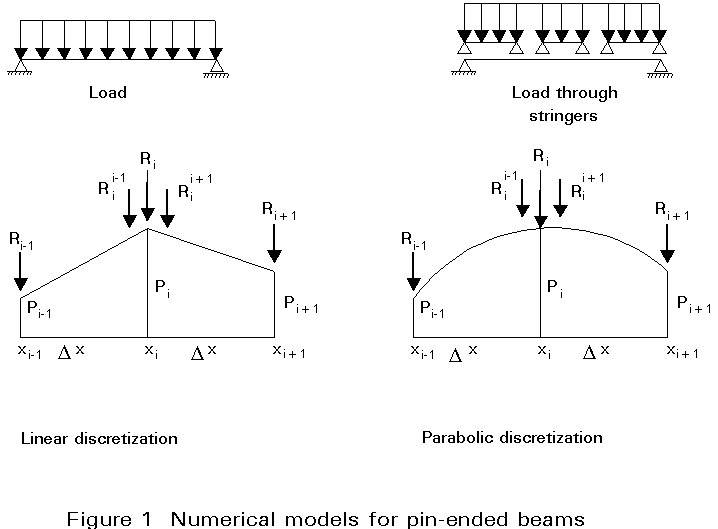
For linear discretization (Figure 1), the formulae are:
End stations: Ri±1 = Dx (2pi±1 + pi) / 6
Intermediate stations:
Rii±1 = Dx (2pi + pi±1) / 6
Ri = Rii+1 + Rii-1 = Dx (pi-1+ 4pi + pi+1) / 6
For parabolic descretization (Figure 1), the formulae are:
Ri±1 = Dx (7pi±1 + 6pi - pi-1) / 24
Rii±1 = Dx (3pi±1 + 10pi - pi-1) / 24
Ri = Rii+1 + Rii-1 = Dx (pi-1 + 10pi + pi+1) / 12
When the loading contains distributed loads the method determines directly the average shears in the segments and the bending moments at the stations. A simple addition gives the shears at the stations. All these values are exact provided that no error is introduced by the load discretisation.
Once the bending moments are known it is possible to compute the curvatures by dividing by the bending stiffness EI. Since the load (p), shear (V) and bending moment (M) bear the same relations to each other as the curvature (c = M/EI) , slope (q) and deflection (y), it may be concluded that the procedure used to compute bending moments from loads can also be used to compute deflections from curvatures, as long as account is taken for the different boundary conditions. In order to repeat the procedure mentioned above, the first step is to replace the curvatures (a continuously distributed quantity) by equivalent "concentrated curvatures". Physically, these quantities represent the sudden changes in slope that take place at the nodes of an hypothetical beam formed by rigid segments hinged to each other and with a bending stiffness provided exclusively by rotational springs placed at the hinges. The changes in slope are equivalent to the distributed curvatures in the sense that they produce the same slopes and deflections at the stations. The formulae for computing the equivalent concentrated curvatures are the ones used for the loads and shown in Figure 1b. Next the procedure yields successively average slopes in the segments and deflections at the stations. It should be noted that these quantities are precisely the equivalent concentrated loads, average shears and bending moments of the "conjugate beam" when acted on by distributed loads which coincide with the curvature diagram of the original beam (the concept of "concentrated curvature" is replaced by the definition of the "conjugate beam").
Finally, in the case of statically indeterminate beams, Newmark's method is well suited to the use of the force method, since it provides a straightforward way of determining the flexibility matrix and the deflections in the basic system.
Whenever Vianello's method is applied to axially loaded columns and step (iii) is performed by means of Newmark's method, one has the method of Vianello-Newmark. Concerning step (ii), i.e. the computation of the values of the bending moments at the stations in terms of the load parameter and on the basis of the initial estimate of the buckling mode, the following procedure is applicable, which is exact provided that all the axial loads are concentrated at the stations:
(i) Calculate the axial forces (N) in the segments in terms of the axial loads (P) which may be expressed in terms of a single load parameter l. If the column is statically indeterminate in the axial direction the values of N must be determined by means of a suitable method (e.g. force method).
(ii) Calculate the values of deflection minus the increment in deflection taking place in each segment, on the basis of the initial estimate (Dyij = yi - yj). This sign convention is adopted so that all the quantities may still be added when proceeding from left to right across the beam and subtracted in the opposite case.
(iii) Calculate the increment in bending moment due to the axial force taking place in each segment (DMij = Nij Dyij).
(iv) Calculate the bending moments, due to the axial forces, at the stations (M¢) by adding or subtracting the values of DM. These bending moments do not include the influence of the support reactions, and therefore, need to be corrected whenever this influence is present.
(v) Perform the appropriate corrections on the bending moments calculated in (iv). These corrections are identical to the ones discussed in the previous chapter and lead to exact values in the case of statically determinate (in the transverse direction) columns. If the column is statically indeterminate and assuming that the force method is used, the procedure described above is performed in the basic system chosen. The compatibility is enforced during step (iii) of Vianello's method, which also uses Newmark's technique, and enables the determination of the bending moments and deflections at the stations of the original column.
If distributed axial loads are present, they must be replaced by equivalent concentrated axial loads (pdisc) using the formulae given in Figure 1b. The procedure of calculating the bending moments at the stations just mentioned then becomes approximate (the error can be reduced by increasing the number of segments).
It should be noted that the calculation of the equivalent concentrated curvatures is now always approximate. Thus the method of Vianello-Newmark will lead to a value of the critical buckling load slightly different from the exact one. This error will be decreased by an increase in the number of segments.
The methods of Vianello and Vianello-Newmark may also be used to determine equilibrium configurations of geometrically imperfect or transversally loaded columns under the action of specified axial loads. Only the method of Vianello-Newmark is discussed below. Vianello's method can be applied only in very simple cases.
For instance, the behaviour of a beam-column is given by the solution of the following differential equation (N piecewise constant):
(5)
The application of the method of Vianello-Newmark consists of an iterative procedure which requires an initial guess of the deflected shape of the beam-column. It converges to the corresponding exact shape y(x). Each iteration involves the solution of the following two equations:
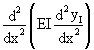= q (6)
= 
(7)
Equation (6) is a standard linear analysis and only needs to be solved once, since yI (x) is the same in all iterations. Equation (7) strongly resembles the eigenvalue-eigenfunction problem dealt with before, the difference residing in the fact that the axial forces are now due to known applied forces. The amplitude of the initial estimates of the deflected shape must, therefore, be controlled by a factor D, determined at the end of each iteration by the condition
(8)
where n is the number of stations. This condition imposes a similarity between the initial and calculated deflected shapes, in the sense that the sum of their station values must be the same.
If the initial imperfection consists of an eccentricity e0 of all the applied loads, then yI (x) is the solution of (N piecewise constant):
Finally, it should be mentioned that the method will diverge if the axial loading parameter l is larger than the corresponding critical value lcr.