
ESDEP WG 8
PLATES AND SHELLS
To discuss the load distribution, stability and ultimate resistance of stiffened plates under in-plane and out-of-plane loading.
Lecture 8.1: Introduction to Plate Behaviour and Design
Lecture 8.2: Behaviour and Design of Unstiffened Plates
Lecture 8.4.1: Plate Girder Behaviour & Design I
Lecture 8.6: Introduction to Shell Structures
The load distribution for in-plane loaded unstiffened plate structures is discussed and the critical buckling loads derived using linear elastic theory. Two design approaches for determining the ultimate resistance of stiffened plates are described and compared. Out-of-plane loading is also considered and its influence on stability discussed. The requirements for finite element models of stiffened plates are outlined using those for unstiffened plates as a basis.
The automation of welding procedures and the need to design elements not only to have the necessary resistance to external actions but also to meet aesthetic and serviceability requirements leads to an increased tendency to employ thin-walled, plated structures, especially when the use of rolled sections is excluded, due to the form and the size of the structure. Through appropriate selection of plate thicknesses, steel qualities and form and position of stiffeners, cross-sections can be best adapted to the actions applied and the serviceability conditions, thus saving material weight. Examples of such structures, shown in Figure 1, are webs of plate girders, flanges of plate girders, the walls of box girders, thin-walled roofing, facades, etc.

Plated elements carry simultaneously:
a) actions normal to their plane,
b) in-plane actions.
Out-of-plane action is of secondary importance for such steel elements since, due to the typically small plate thicknesses involved, they are not generally used for carrying transverse actions. In-plane action, however, has significant importance in plated structures.
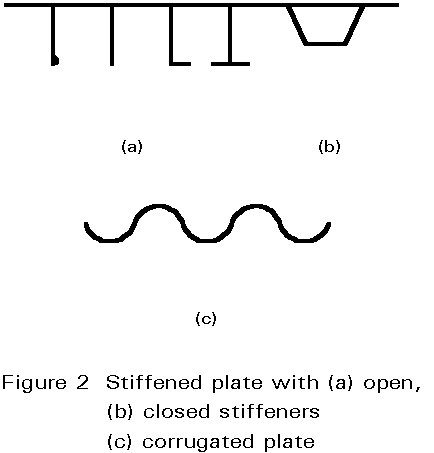
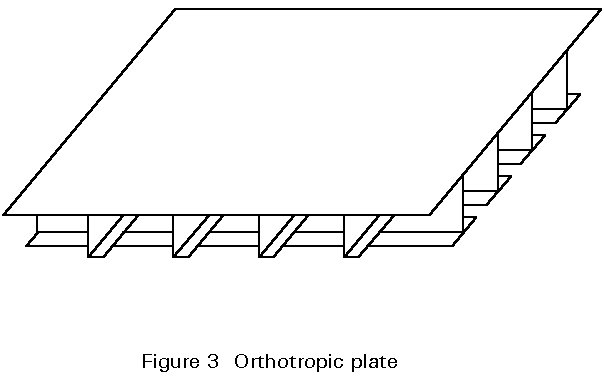
The intention of design is to utilise the full strength of the material. Since the slenderness of such plated elements is large due to the small thicknesses, their carrying resistance is reduced due to buckling. An economic design may, however, be achieved when longitudinal and/or transverse stiffeners are provided. Such stiffeners may be of open or of torsionally rigid closed sections, as shown in Figure 2. When these stiffeners are arranged in a regular orthogonal grid, and the spacing is small enough to 'smear' the stiffeners to a continuum in the analysis, such a stiffened plate is called an orthogonal anisotropic plate or in short, an orthotropic plate (Figure 3). In this lecture the buckling behaviour of stiffened plate panels subjected to in-plane actions will be presented. The behaviour under out-of-plane actions is also discussed as is the influence of the out-of-plane action on the stability of stiffened plates.
Specific topics such as local actions and the tension field method are covered in the lectures on plate girders.
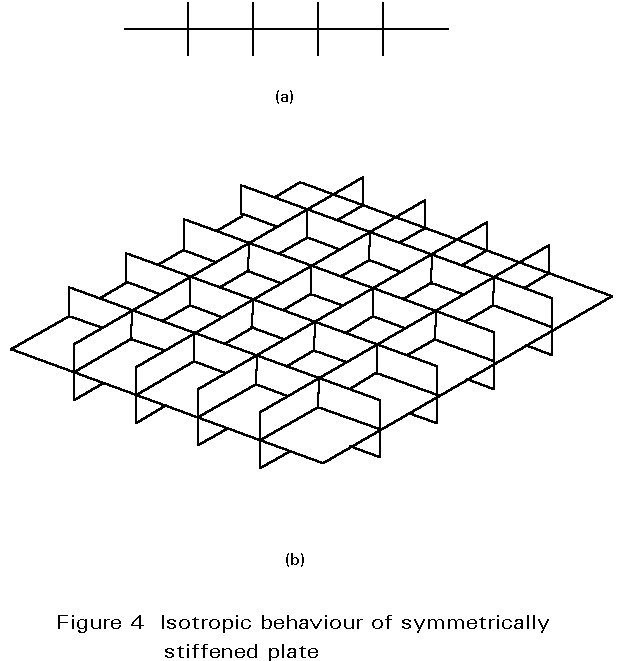
The stress distribution can be determined from the solutions of Navier's equations (see Lecture 8.2 Section 2.1.1) but, for stiffened plates, this is limited to plates where the longitudinal and transverse stiffeners are closely spaced, symmetrical to both sides of the plate, and produce equal stiffness in the longitudinal and transverse direction, see Figure 4. This configuration leads to an isotropic behaviour when the stiffeners are smeared out. In practice this way of stiffening is not practical and therefore not commonly used.
All deviations from the "ideal" situation (eccentric stiffeners, etc.) have to be taken into account when calculating the stress distribution in the plate.
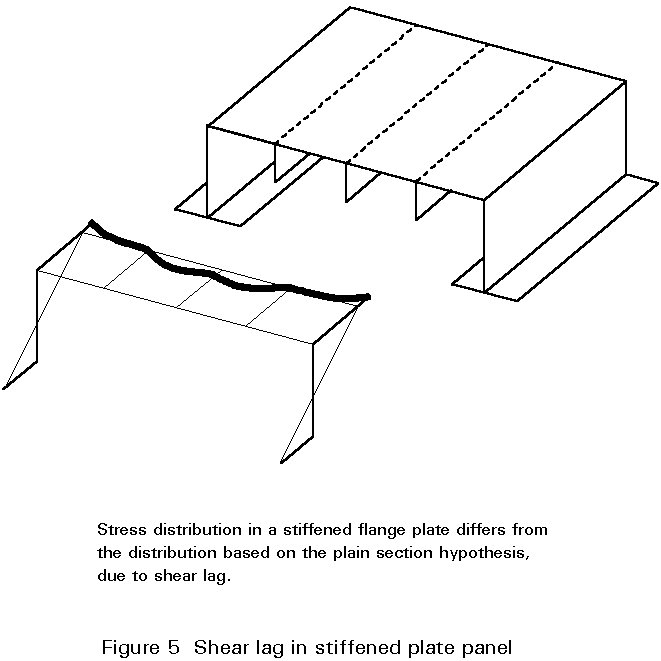
As for unstiffened plates the most practical way of determining the stress distribution in the panel is using the plane strain hypothesis. Since stiffened plates have a relatively large width, however, the real stress distribution can differ substantially from the calculated stress distribution due to the effect of shear lag.
Shear lag may be taken into account by a reduced flange width concentrated along the edges and around stiffeners in the direction of the action (see Figure 5).
The stiffeners can be modelled as beam-column elements eccentrically attached to the plate elements, see Lecture 8.2, Section 2.1.3.
In the case where the stiffeners are relatively deep beams (with large webs) it is better to model the webs with plate elements and the flange, if present, with a beam-column element.
The knowledge of the critical buckling load for stiffened plates is of importance not only because design was (and to a limited extent still is) based on it, but also because it is used as a parameter in modern design procedures. The assumptions for the linear buckling theory of plates are as follows:
a) the plate is perfectly plane and stress free.
b) the stiffeners are perfectly straight.
c) the loading is absolutely concentric.
d) the material is linear elastic.
e) the transverse displacements are relatively small.
The equilibrium path has a bifurcation point which corresponds to the critical action (Figure 6).
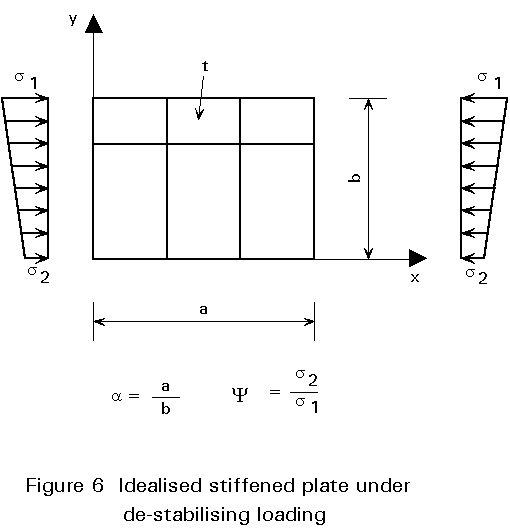
Analytical solutions, through direct integration of the governing differential equations are, for stiffened plates, only possible in specific cases; therefore, approximate numerical methods are generally used. Of greatest importance in this respect is the Rayleigh-Ritz approach, which is based on the energy method. If Po, and PI represent the total potential energy of the plate in the undeformed initial state and at the bifurcation point respectively (Figure 6), then the application of the principle of virtual displacements leads to the expression:
d
(PI) = d(Po + DPo) = d(Po + dPo +since PI is in equilibrium. But the initial state is also in equilibrium and therefore dPo = 0. The stability condition then becomes:
d
(d2Po) = 0 (2)d2Po in the case of stiffened plates includes the strain energy of the plate and the stiffeners and the potential of the external forces acting on them. The stiffeners are characterized by three dimensionless coefficients d, g, υ expressing their relative rigidities for extension, flexure and torsion respectively.
For rectangular plates simply supported on all sides (Figure 6) the transverse displacements in the buckled state can be approximated by the double Fourier series:
![]() (3)
(3)
which complies with the boundary conditions. The stability criterion, Equation (2), then becomes:
![]() (4)
(4)
since the only unknown parameters are the amplitudes amn, Equations (4) form a set of linear and homogeneous linear equations, the number of which is equal to the number of non-zero coefficients amn retained in the Ritz-expansion. Setting the determinant of the coefficients equal to 0 yields the buckling equations. The smallest Eigenvalue is the so-called buckling coefficient k. The critical buckling load is then given by the expression:
s
cr = kssE or tcr = ktsE (5)with sE =![]()
The most extensive studies on rectangular, simply supported stiffened plates were carried out by Klöppel and Scheer[1] and Klöppel and Möller[2]. They give charts, as shown in Figure 7, for the determination of k as a function of the coefficients d and g, previously described, and the parameters a = a/b and y =s2/s1 as defined in Figure 6a. Some solutions also exist for specific cases of plates with fully restrained edges, stiffeners with substantial torsional rigidity, etc. For relevant literature the reader is referred to books by Petersen[3] and by Dubas and Gehri[4].
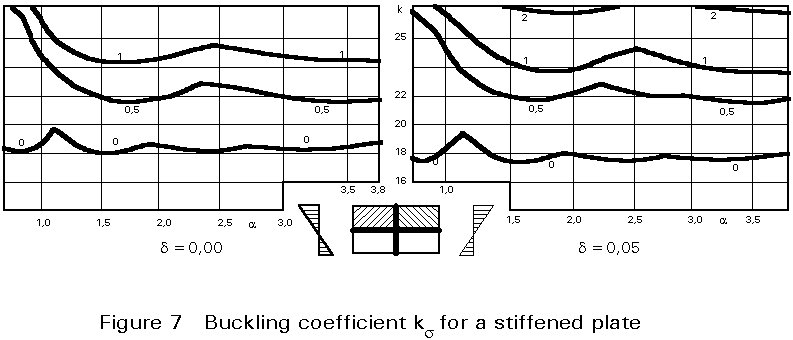
When the number of stiffeners in one direction exceeds two, the numerical effort required to determine k becomes considerable; for example, a plate panel with 2 longitudinal and 2 transverse stiffeners requires a Ritz expansion of 120. Practical solutions may be found by "smearing" the stiffeners over the entire plate. The plate then behaves orthotropically, and the buckling coefficient may be determined by the same procedure as described before.
An alternative to stiffened plates, with a large number of equally spaced stiffeners and the associated high welding costs, are corrugated plates, see Figure 2c. These plates may also be treated as orthotropic plates, using equivalent orthotropic rigidities[5].
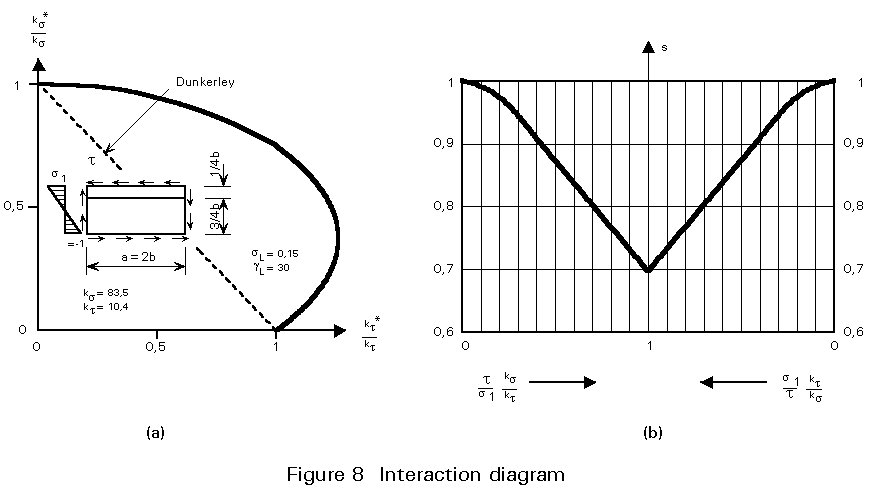
So far only the application of simple action has been considered. For combinations of normal and shear stresses a linear interaction, as described by Dunkerley, is very conservative. On the other hand direct determination of the buckling coefficient fails due to the very large number of combinations that must be considered. An approximate method has, therefore, been developed, which is based on the corresponding interaction for unstiffened plates, provided that the stiffeners are so stiff that buckling in an unstiffened sub-panel occurs before buckling of the stiffened plate. The critical buckling stress is determined for such cases by the expression:
s
vcr = ks Z1s sE (6)where sE has the same meaning as in Equation (5).
s is given by charts (Figure 8b).
Z1 = ![]()
ks , kt are the buckling coefficients for normal and shear stresses acting independently
For more details the reader is referred to the publications previously mentioned.
Optimum rigidity of stiffeners
Three types of optimum rigidity of stiffeners g*, based on linear buckling theory, are usually defined[6]. The first type gI*, is defined such that for values g > gI* no further increase of k is possible, as shown in Figure 9a, because for g = gI* the stiffeners remain straight.

The second type gII*, is defined as the value for which two curves of the buckling coefficients, belonging to different numbers of waves, cross (Figure 9b). The buckling coefficient for g < gII* reduces considerably, whereas it increases slightly for g > gII*. A stiffener with g = gII* deforms at the same time as the plate buckles.
The third type gIII* is defined such that the buckling coefficient of the stiffened plate becomes equal to the buckling coefficient of the most critical unstiffened subpanel (Figure 9c).
The procedure to determine the optimum or critical stiffness is, therefore, quite simple. However, due to initial imperfections of both plate and stiffeners as a result of out of straightness and welding stresses, the use of stiffeners with critical stiffness will not guarantee that the stiffeners will remain straight when the adjacent unstiffened plate panels buckle.
This problem can be overcome by multiplying the optimum (critical) stiffness by a factor, m, when designing the stiffeners.
The factor is often taken as m = 2,5 for stiffeners which form a closed cross-section together with the plate, and as m = 4 for stiffeners with an open cross-section such as flat, angle and T-stiffeners.
Behaviour of Stiffened Plates
Much theoretical and experimental research has been devoted to the investigation of stiffened plates. This research was intensified after the collapses, in the 1970's, of 4 major steel bridges in Austria, Australia, Germany and the UK, caused by plate buckling. It became evident very soon that linear buckling theory cannot accurately describe the real behaviour of stiffened plates. The main reason for this is its inability to take the following into account:
a) the influence of geometric imperfections and residual welding stresses.
b) the influence of large deformations and therefore the post buckling behaviour.
c) the influence of plastic deformations due to yielding of the material.
d) the possibility of stiffener failure.
Concerning the influence of imperfections, it is known that their presence adversely affects the carrying resistance of the plates, especially in the range of moderate slenderness and for normal compressive (not shear) stresses.
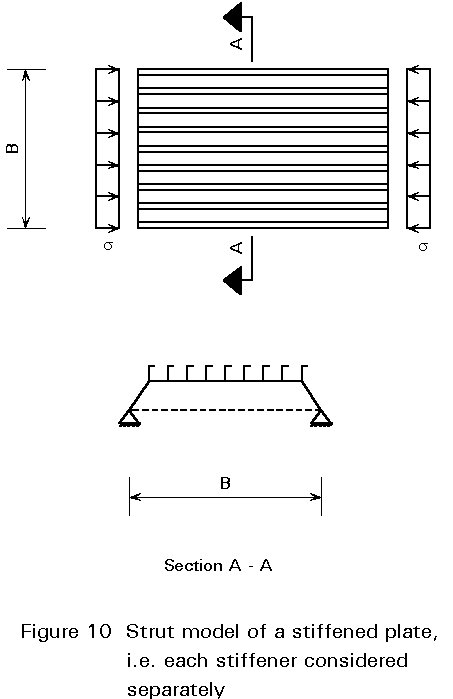
Large deformations, on the other hand, generally allow the plate to carry loads in the post-critical range, thus increasing the action carrying resistance, especially in the range of large slenderness. The post-buckling behaviour exhibited by unstiffened panels, however, is not always present in stiffened plates. Take, for example, a stiffened flange of a box girder under compression, as shown in Figure 10. Since the overall width of this panel, measured as the distance between the supporting webs, is generally large, the influence of the longitudinal supports is rather small. Therefore, the behaviour of this flange resembles more that of a strut under compression than that of a plate. This stiffened plate does not, accordingly, possess post-buckling resistance.
As in unstiffened panels, plastic deformations play an increasingly important role as the slenderness decreases, producing smaller ultimate actions.
The example of a stiffened plate under compression, as shown in Figure 11, is used to illustrate why linear bucking theory is not able to predict the stiffener failure mode. For this plate two different modes of failure may be observed: the first mode is associated with buckling failure of the plate panel; the second with torsional buckling failure of the stiffeners. The overall deformations after buckling are directed in the first case towards the stiffeners, and in the second towards the plate panels, due to the up or downward movement of the centroid of the middle cross-section. Experimental investigations on stiffened panels have shown that the stiffener failure mode is much more critical for both open and closed stiffeners as it generally leads to smaller ultimate loads and sudden collapse. Accordingly, not only the magnitude but also the direction of the imperfections is of importance.
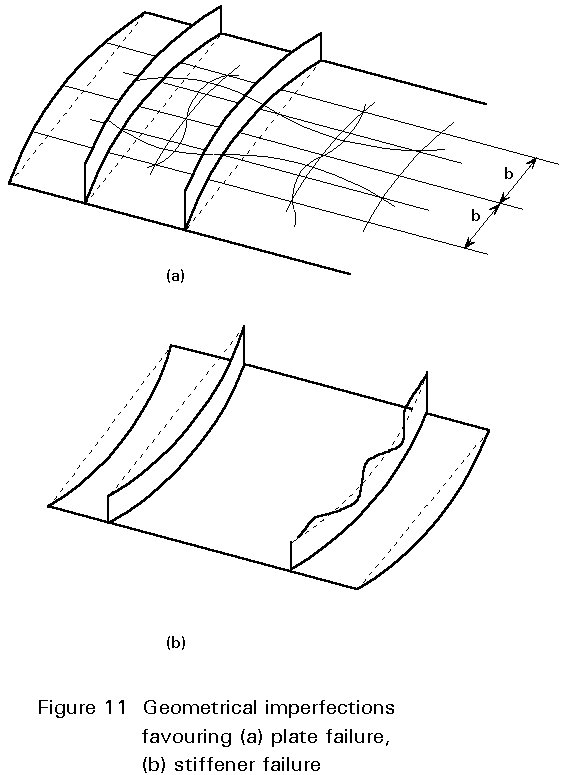
Due to the above mentioned deficiencies in the way that linear buckling theory describes the behaviour of stiffened panels, two different design approaches have been recently developed. The first, as initially formulated by the ECCS-Recommendations [7] for allowable stress design and later expanded by DIN 18800, part 3[8] to ultimate limit state design, still uses values from linear buckling theory for stiffened plates. The second, as formulated by recent Drafts of ECCS-Recommendations [9,10], is based instead on various simple limit state models for specific geometric configurations and loading conditions. Both approaches have been checked against experimental and theoretical results; they will now be briefly presented and discussed.
Design Approach with Values from the Linear Buckling Theory
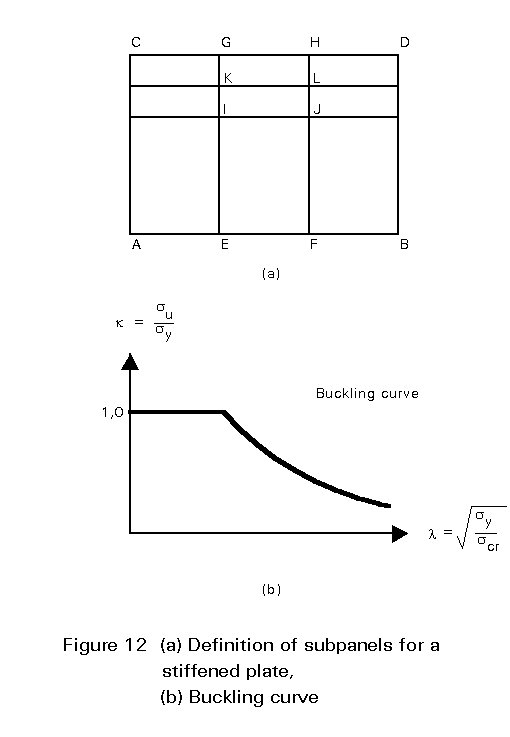
With reference to a stiffened plate supported along its edges (Figure 12), distinction is made between individual panels, e.g. IJKL, partial panels, i.e. EFGH, and the overall panel ABCD. The design is based on the condition that the design stresses of all the panels shall not exceed the corresponding design resistances. The adjustment of the linear buckling theory to the real behaviour of stiffened plates is basically made by the following provisions:
a) Introduction of buckling curves as illustrated in Figure 12b.
b) Consideration of effective widths, due to local buckling, for flanges associated with stiffeners.
c) Interaction formulae for the simultaneous presence of stresses sx, sy and t at the ultimate limit state.
d) Additional reduction factors for the strut behaviour of the plate.
e) Provision of stiffeners with minimum torsional rigidities in order to prevent lateral-torsional buckling.
Design Approach with Simple Limit State Models
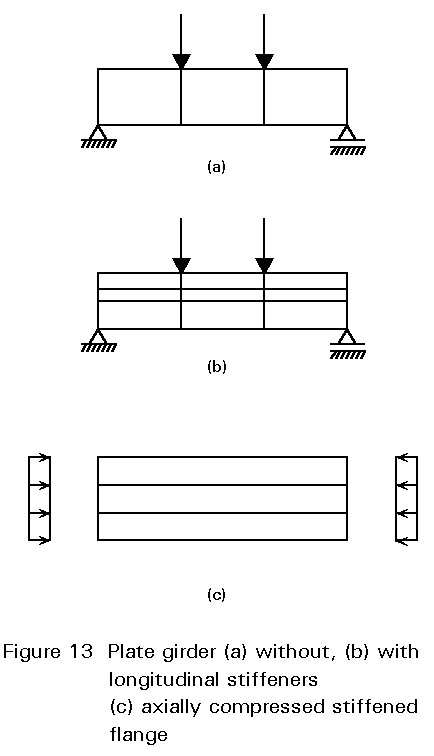
Drafts of European Codes and Recommendations have been published which cover the design of the following elements:
a) Plate girders with transverse stiffeners only (Figure 13a) - Eurocode 3 [11].
b) Longitudinally stiffened webs of plate and box girders (Figure 13b) - ECCS-TWG 8.3, 1989.
c) Stiffened compression flanges of box girders (Figure 13c) - ECCS [10].
Only a brief outline of the proposed models is presented here; for more details reference should be made to Lectures 8.4, 8.5, and 8.6 on plate girders and on box girders:
The stiffened plate can be considered as a grillage of beam-columns loaded in compression. For simplicity the unstiffened plates are neglected in the ultimate resistance and only transfer the loads to the beam-columns which consist of the stiffeners themselves together with the adjacent effective plate widths. This effective plate width is determined by buckling of the unstiffened plates (see Section 2.2.1 of Lecture 8.2). The bending resistance Mu, reduced as necessary due to the presence of axial forces, is determined using the characteristics of the effective cross-section. Where both shear forces and bending moments are present simultaneously an interaction formula is given. For more details reference should be made to the original recommendations.
The resistance of a box girder flange subjected to compression can be determined using the method presented in the ECCS Recommendations referred to previously, by considering a strut composed of a stiffener and an associated effective width of plating. The design resistance is calculated using the Perry-Robertson formula. Shear forces due to torsion or beam shear are taken into account by reducing the yield strength of the material according to the von Mises yield criterion. An alternative approach using orthotropic plate properties is also given.
The above approaches use results of the linear buckling theory of unstiffened plates (value of Vcr, determination of beff etc.). For stiffened plates the values given by this theory are used only for the expression of the rigidity requirements for stiffeners. Generally this approach gives rigidity and strength requirements for the stiffeners which are stricter than those mentioned previously in this lecture.
Discussion of the Design Approaches
Both approaches have advantages and disadvantages.
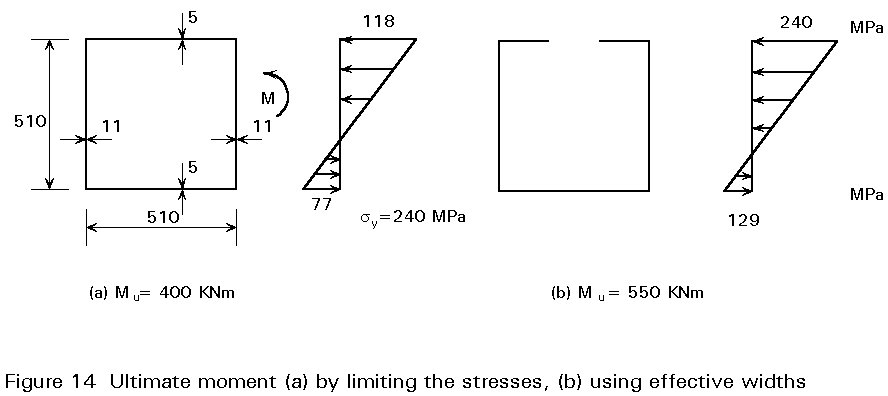
The main advantage of the first approach is that it covers the design of both unstiffened and stiffened plates subjected to virtually any possible combination of actions using the same method. Its main disadvantage is that it is based on the limitation of stresses and, therefore, does not allow for any plastic redistribution at the cross-section. This is illustrated by the example shown in Figure 14. For the box section of Figure 14a, subjected to a bending moment, the ultimate bending resistance is to be determined. If the design criterion is the limitation of the stresses in the compression thin-walled flange, as required by the first approach, the resistance is Mu = 400kNm. If the computation is performed with effective widths that allow for plastic deformations of the flange, Mu is found equal to 550kNm.
The second approach also has some disadvantages: there are a limited number of cases of geometrical and loading configurations where these models apply; there are different methodologies used in the design of each specific case and considerable numerical effort is required, especially using the tension field method.
Another important point is the fact that reference is made to webs and flanges that cannot always be defined clearly, as shown in the examples of Figure 15.
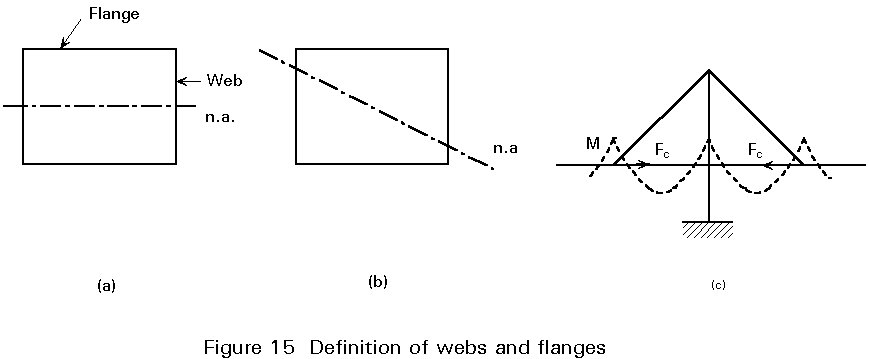
For a box girder subjected to uniaxial bending (Figure 15a) the compression flange and the webs are defined. This is however not possible when biaxial bending is present (Figure 15b). Another example is shown in Figure 15c; the cross-section of a cable stayed bridge at the location A-A is subjected to normal forces without bending; it is evident, in this case, that the entire section consists of "flanges".
Finite Element Methods
In determining the stability behaviour of stiffened plate panels, basically the same considerations hold as described in Lecture 8.2, Section 2.2.2. In addition it should be noted that the stiffeners have to be modelled by shell elements or by a combination of shell and beam-column elements. Special attention must also be given to the initial imperfect shape of the stiffeners with open cross-sections.
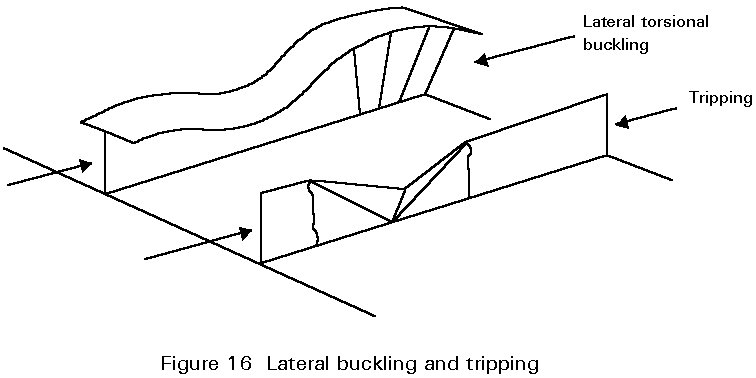
It is difficult to describe all possible failure modes within one and the same finite element model. It is easier, therefore, to describe the beam-column behaviour of the stiffeners together with the local and overall buckling of the unstiffened plate panels and the stiffened assemblage respectively and to verify specific items such as lateral-torsional buckling separately (see Figure 16). Only for research purposes is it sometimes necessary to model the complete structure such that all the possible phenomena are simulated by the finite element model.
The theory described in Section 3.1.1 of Lecture 8.2 can only be applied to stiffened plates if the stiffeners are sufficiently closely spaced so that orthotropic behaviour occurs. If this is not the case it is better to consider the unstiffened plate panels in between the stiffeners separately. The remaining grillage of stiffeners must be considered as a beam system in bending (see Section 3.1.2).
The unstiffened sub-panels can be analysed as described in Section 3.1.1 of Lecture 8.2.
The remaining beam grillage is formed by the stiffeners which are welded to the plate, together with a certain part of the plate. The part can be taken as for buckling, namely the effective width as described in Section 2.2.2 of this Lecture. In this way the distribution of forces and moments can be determined quite easily.
Similar considerations hold for using FEM to determine the force and moment distribution in stiffened plates which are subject to out-of-plane actions as for using FEM for stiffened plates loaded in-plane (see Section 2.1.3) except that the finite elements used must be able to take large deflections and elastic-plastic material behaviour into account.
All considerations mentioned in Section 3.2 of Lecture 8.2 for unstiffened plates are valid for the analysis of stiffened plates both for deflections and ultimate resistance. It should be noted, however, that for design purposes it is easier to verify specific items, such as lateral-torsional buckling, separately from plate buckling and beam-column behaviour.
The points made in Section 4 of Lecture 8.2 also apply here; that is, the stability of the stiffened plate is unfavourably influenced if the deflections, due to out-of-plane actions, are similar to the stability collapse mode.
[1] Klöppel, K., Scheer, J., "Beulwerte Ausgesteifter Rechteckplatten", Bd. 1, Berlin, W. Ernst u. Sohn 1960.
[2] Klöppel, K., Möller, K. H., "Beulwerte Ausgesteifter Rechteckplatten", Bd. 2, Berlin, W. Ernst u. Sohn 1968.
[3] Petersen, C., "Statik und Stabilität der Baukonstruktionen", Braunschweig: Vieweg 1982.
[4] Dubas, P., Gehri, E., "Behaviour and Design of Steel Plated Structures", ECCS, 1986.
[5] Briassoulis, D., "Equivalent Orthotropic Properties of Corrugated Sheets", Computers and Structures, 1986, 129-138.
[6] Chwalla, E., "Uber die Biegungsbeulung der langsversteiften Platte und das Problem der Mindeststeifigeit", Stahlbau 17, 1944, 84-88.
[7] ECCS, "Conventional design rules based on the linear buckling theory", 1978.
[8] DIN 18800 Teil 3 (1990), "Stahlbauten, Stabilitätsfalle, Plattenbeulen", Berlin: Beuth.
[9] ECCS, "Design of longitudinally stiffened webs of plate and box girders", Draft 1989.
[10] ECCS, "Stiffened compression flanges of box girders", Draft 1989.
[11] Eurocode 3, "Design of Steel Structures": ENV 1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.