ESDEP WG 7

ELEMENTS

Lecture 7.6: Built-up Columns

OBJECTIVE/SCOPE

To derive the equations for the buckling loads of built-up columns and to present the design methods used in Eurocode 3 [1].

PREREQUISITES

Lectures 6: Applied Stability

Lectures 7.5: Columns

RELATE WORKED EXAMPLES

Worked Example 7.6: Built-Up Columns

SUMMARY

This lecture is divided into two main parts; the first part concentrates on the influence of shear deformations on the elastic critical loads and on the slenderness of columns (this effect is crucial for built-up columns and secondary for solid columns - rolled or welded shapes); the second part deals with the design approach adopted in Eurocode 3 [1] which is related to experimental behaviour.

1. INTRODUCTION

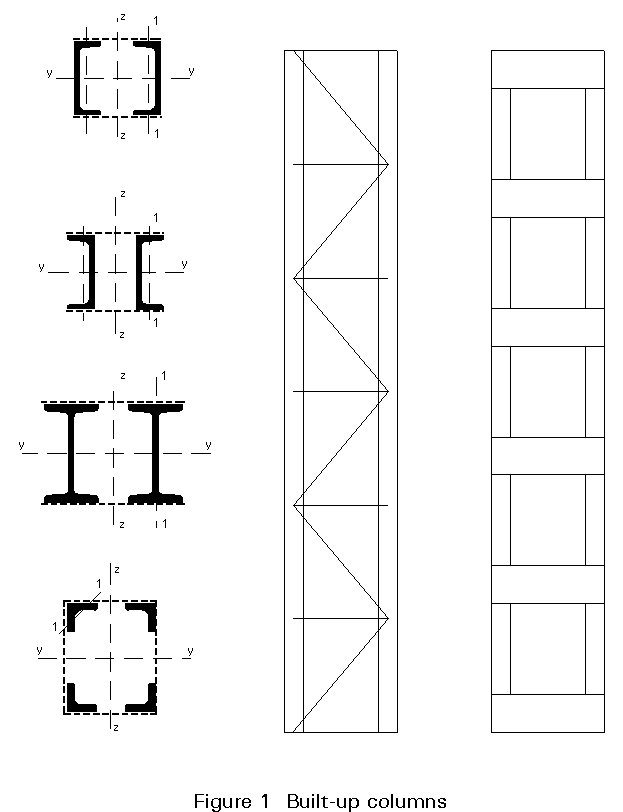
Built-up columns are widely used in steel construction especially when the effective lengths are great and the compression forces light. They are composed of two or more parallel main components interconnected by lacing or batten plates (Figures 1 and 2). The greater the distance between the chord axes, the greater is the moment of inertia of the built-up cross section; the increase in stiffness, however, is counterbalanced by the increased weight and cost of the connection of members.

It should be noted that built-up columns (especially battened built-up columns) are more flexible than solid columns with the same moment of inertia; this must be taken into account in the design.

In order to derive the carrying capacity of steel built-up columns, the following must be studied:

the elastic buckling load and the global behaviour;
the local behaviour of the chords;
the internal forces in the connecting members.

2. THE EFFECT OF SHEAR DEFORMATIONS ON THE ELASTIC CRITICAL COLUMN LOAD

This section discusses the effect of shear deformation on the elastic critical column load.

The simple case of a pin-ended column, shown in Figure 3, is considered; for M, N, V, x and y, as defined in this Figure, the following relationships hold:

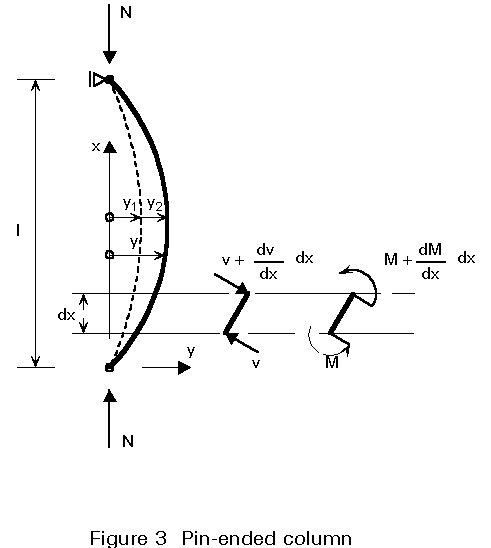
M = N y, (2.1)

The total lateral deflection y of the centreline is the result of two components:

y = y₁ + y₂ (2.2)

the bending moment M gives rise to the deflection y₁, and the shearing force V to the additional deflection y₂.

According to elastic theory the curvature due to the bending moment M is as follows:

(2.3)

where

E is the modulus of elasticity or Young's modulus.

I is the moment of inertia of the cross-section.

The slope due to the shearing force V is as follows:

(2.4)

where

A is the cross-sectional area.

G is the modulus of rigidity or shear modulus.

b is the shape factor of the column cross-section (b =1,11 for solid circular cross-sections; b = 1,2 for rectangular cross-sections).

The curvature due to the effect of the shearing force V is as follows:

(2.5)

The total curvature of the buckling curve is due both to the bending moment, Equation (2.3), and to the shearing force, Equation (2.5):

(2.6)

It is possible to rearrange Equation (2.6) in the form:

(2.7)

Adopting the same procedure as in the Euler case, the critical load is defined by the equation:

(2.8)

Solving for N, the following expression for the elastic critical load N_cr,id is obtained:

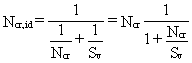(2.9)

where:

N_cr = is the Euler buckling load obtained disregarding the deformations due to shearing force

S_v = is the shear stiffness of the column.

Obviously N_cr,id < N_cr ; the greater the ratio N_cr / S_v, the smaller the ratio N_cr,id/ N_cr < 1. The ratio N_cr,id / N_cr obtained from Equation (2.9) is plotted, in Figure 4, as a function of the ratio N_cr / S_v.

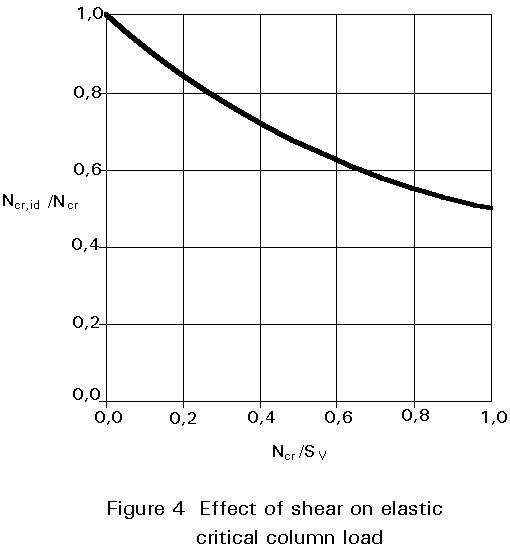
For solid rolled cross-sections the shear stiffness S_v is much greater than N. The difference between N_cr,id and N_cr is very small therefore, and can be disregarded for design purposes.

However, as will be shown below, the shear stiffness S_v, of built-up columns, is much smaller than it is for solid shapes; in this case, therefore, the influence of the shearing forces on the reduction of the critical load is very significant.

In order to compare the shear stiffness S_v to the Euler buckling loads of solid columns N_cr, consider as an example a HE200A column buckling in the plane of the web.

The shear stiffness S_v is as follows:

S_v =

E = 200 kNmm^-2

n = 0,3

A_w = the area of the web = 6,5 x 170 = 1105 mm²

The Euler buckling load N_cr is:

N_cr =

where:

A is the cross-sectional area = 5380 mm².

l is the slenderness of the column.

In Table 1 the critical buckling loads N_cr,id, the Euler buckling loads N_cr, and the ratios N_cr / S_v are given as functions of the slenderness; it clearly shows that in the case of solid cross-sections, N_cr is always far smaller than S_v; therefore, for technical purposes, it is possible to disregard the influence of the shear deformations on the elastic buckling loads N_cr,id.

3. EVALUATION OF THE SHEAR STIFFNESS OF LACED AND BATTENED COLUMNS

3.1 Laced Columns

In laced columns the elastic extension of the diagonals and the horizontals must be considered in order to derive the shear stiffness S_v; the elongation of the chords (the main components) should not be taken into account, because they are already considered in the global flexural stiffness E I of the built-up column.

With an N-shape arrangement of lacing, as shown in Figure 5, the elongations of one diagonal and of one horizontal are taken into account in order to derive S_v:

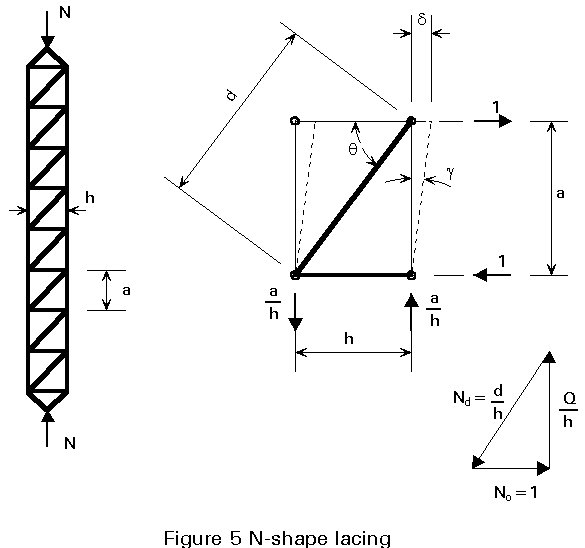
1/S_v = d/a = g (3.1)

where d is the lateral displacement due to the unit shearing force.

The total displacement d is the result of two components: d₁ is the contribution from the elongation of the diagonal; d₂ is the contribution from the shortening of the horizontal. From virtual work theory:

Thus, for one plane of lacing:

(3.2)

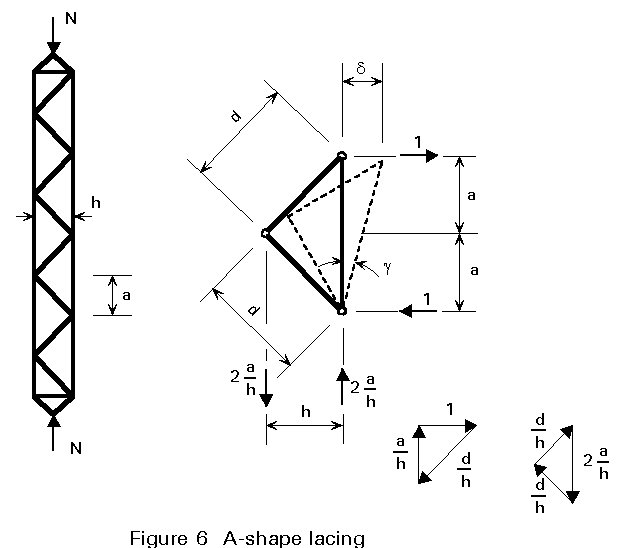
With an A shape arrangement of lacing, as shown in Figure 6:

Therefore:

(3.3)

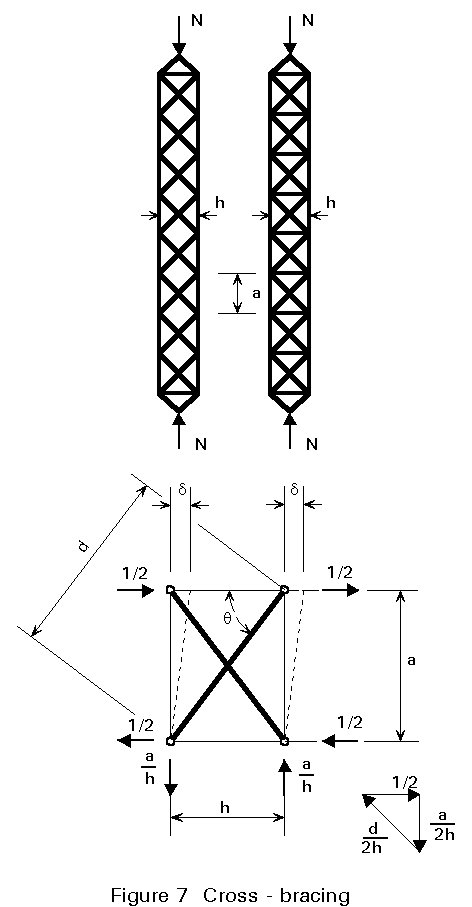
The cross-bracings, shown in Figure 7, have the same shear stiffness, because the horizontals do not take part in the transmission of the shearing force:

and the shear stiffness is:

(3.4)

3.2 Battened Built-up Columns

For battened built-up columns, as shown in Figure 8, the flexural deformations both of the chords and of the battens must be considered in order to derive the shear stiffness S_v; as is the case for laced built-up columns, the extensions of the main chords are not considered because their contributions appear in the global flexural stiffness E I.

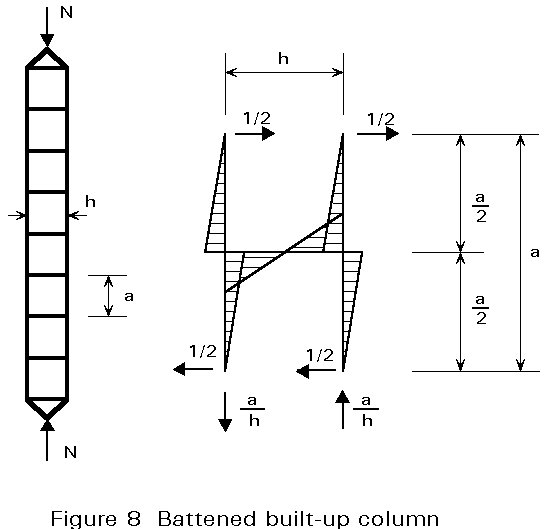
Adopting the virtual work method, the displacement d due to unit shearing force is obtained:

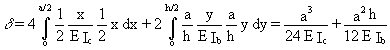
and the shear stiffness is:

(3.5)

where I_c is the in-plane second moment of area of one chord.

I_b is the in-plane second moment of area of one batten.

The above formula may be refined by taking into account the deformations due to the shearing force in the battens.

3.3 Quantitative Comparison

Table 2 gives a comparison of the shear stiffness S_v for a solid column and three different built-up columns; the global dimensions of the cross-sections and the weights of steel per unit length are kept constant.

The solid column (a) is made up of two HE400A shapes each welded to a common plate 8mm thick x 1000mm wide.

Built-up columns (b) and (c) are laced: the chords are HE400A shapes and there are two planes of lacing with 100 ´ 10 equal angles.

Built-up column (d) is with batten plates: the same shape HE400A as above is adopted for the chords; the batten plates, which have rectangular cross-section 400 ´ 20mm, are on two planes.

Whereas the steel employed in the web and in the connecting members has almost the same weight in the four columns, Table 2 shows that the shear stiffness S_v has a wide range of variation.

4. THE ELASTIC CRITICAL LOADS OF BUILT-UP COLUMNS

For design purposes the elastic critical loads of built-up columns can be obtained from Equation (2.9): that is, it is possible to assume a continuous distribution of the shear stiffness S_v if the number of panels is greater than or equal to six; if not, more complex analysis, with methods suitable for frames, has to be performed (for further reading on this topic see (1, 2, and 3).

By introducing formulae for the shear stiffness S_v (3.2, 3.3, 3.4 and 3.5) in Equation (2.9), it is easy to derive, for the various types of lacings and battens, specific formulae for the elastic critical loads N_cr,id and, as a consequence, for the effective length of built-up columns; formulae of this type are widely adopted in the European codes and standards for steel construction.

The details of the analytical procedure are now outlined.

When the lacing is N shaped (as shown in Figure 5), the expression for the shear stiffness S_v (3.2) is substituted in Equation (2.9), where:

N_cr = p² E I / l² is the Euler critical load, as for a solid column.

I = 2 I_c + A_c h², is the moment of inertia of the built-up cross-section.

A_c is the cross-sectional area of the chords.

I_c is the relevant moment of inertia of the chords.

Substitution gives the following:

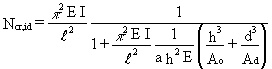(4.1)

By introducing the slenderness l for the column without shear deformations, such that:

l² = 1/ r² = 2 A_c l² /I

the elastic critical stress s_cr,id, for the built-up column becomes:

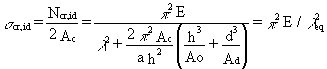(4.2)

where:

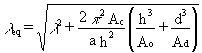(4.3)

is the equivalent slenderness of the built-up column.

Following the same procedure, when simple A bracing (Figure 6) is adopted, the equivalent slenderness of the column is:

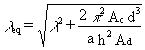(4.4)

For cross-bracing (Figure 7):

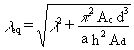(4.5)

Finally, for battened built-up columns (Figure 8), the equivalent slenderness is:

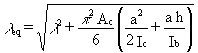(4.6)

If the batten plates are very stiff, their flexural deformations may be disregarded and it is possible to put:

, in Equation (4.6).

In this case the equivalent slenderness of battened built-up columns becomes:

l_eq= Ö{l² + p²A_ca² /(12I_c)} = Ö{l² + p²l₁² /12} (4.7)

where l₁ is the local slenderness of the chords between the centrelines of the batten plates.

5. THE BEARING CAPACITY OF STEEL BUILT-UP COLUMNS AND THE DESIGN PHILOSOPHY OF EUROCODE 3

The experimental behaviour of a steel built-up column (with batten plates) [2] in a compression test up to collapse, is summarised in Figure 9.

in Figure 9(a) the lateral displacement v at midspan is plotted as a function of the applied external compression load N_i.
in Figure 9(b) the axial forces N₁ and N₂ in the chords at midspan are plotted as a function of the compression load N_i.
finally in Figure 9(c) the shearing forces in the batten plates are plotted, and in Figure 9(d) the distribution of the shearing forces in the battens is shown.

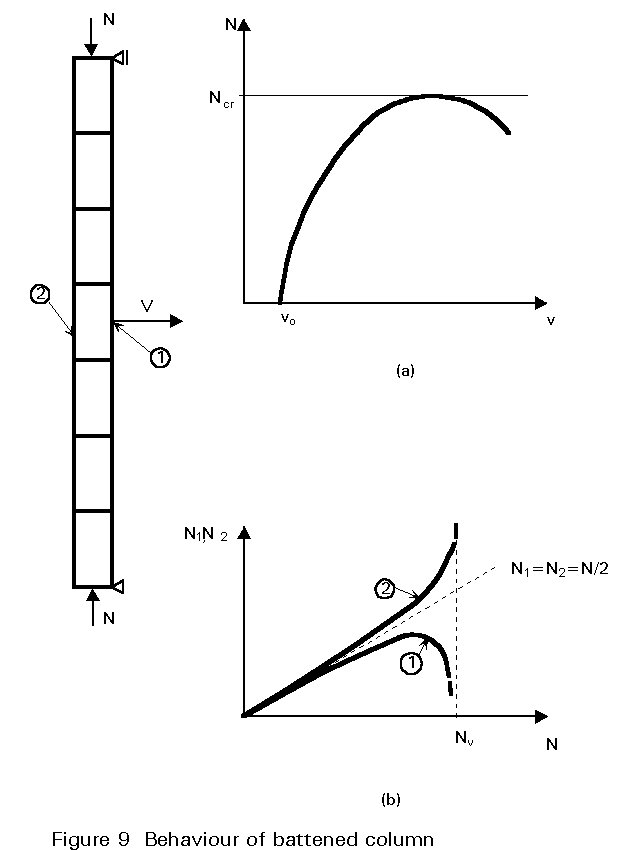
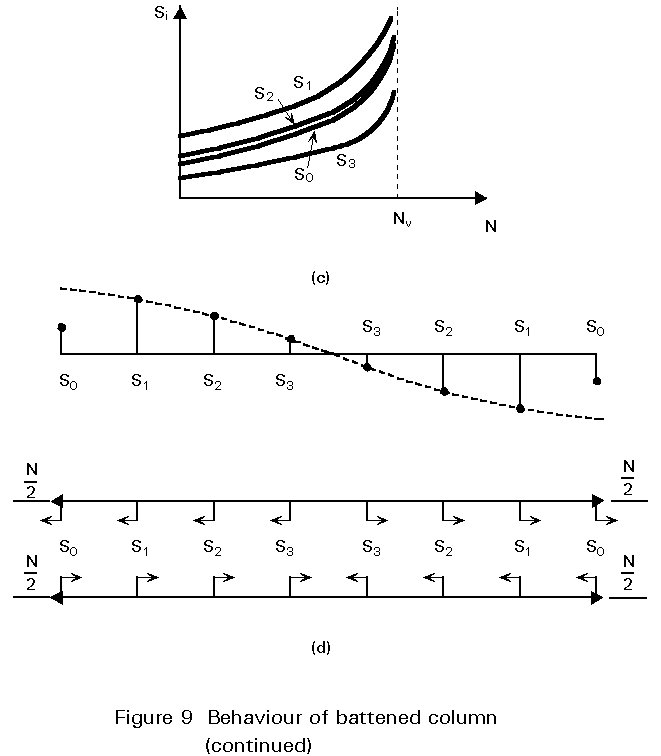
Due to the initial geometrical imperfections and residual stresses, the lateral displacements increase with the applied load more and more rapidly up to the bearing capacity N_cr of the column; the presence of lateral displacements explains why one chord is more compressed than the other, which tends to unload after it has reached maximum compression.

In the batten plate at the end, the framing effect is smaller than in the next internal one, because of the presence of only half a field.

The maximum carrying capacity of the built-up column is reached when one of the following possibilities occurs:

at mid-span the more compressed chord buckles.
at the end a chord fails by compression and flexure.
a batten-plate and/or its connection to the chords fails by shear and flexure.

The main features of the experimental behaviour of a built-up compression member summarised above may be represented by a simple elastic column with equivalent initial geometrical imperfections and shear flexibility (Figure 10).

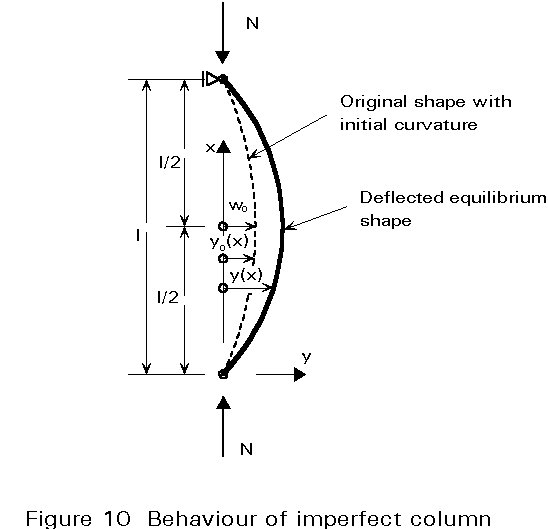
The design philosophy of Eurocode 3 [1] is based on this simple model: it is assumed that in the initial unloaded state the column is not perfectly straight and that the initial deflection y (x) is given by a sine curve for a pin-ended member:

y_o (x) = w_o sin (p x / l) (5.1)

where

w_o is the equivalent geometrical out of straightness at mid-span (w_o = 0,002l = l / 500);

l is the length of the pin-ended column.

When the design axial load N is applied to the built-up column the initial geometrical imperfection is then amplified elastically; the lateral displacements in the equivalent state are:

sin (p x / l) (5.2)

where, in Equation (5.2), N_cr,id is the elastic critical load of the built-up column as given in Section 4.

At mid-span of the built-up column, the axial force is N and the bending moment M equals:

(5.3)

The axial force N_f in the most loaded chord is:

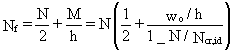(5.4)

The buckling resistance of the chords N_Rd must be greater than N_f:

N_Rd ³ N_f (5.5)

In laced built-up columns the effective length of the chords is taken equal to the system length between lacing connections; in battened built-up columns (for the sake of simplicity and disregarding any possible end restraint) the effective length of the chords is taken equal to the distance between the centre lines of the battens.

The shearing force V at the ends of a built-up column is given by:

(5.6)

The forces in the lacing members and in the chords adjacent to the ends are derived from the shearing force V and from the axial force N.

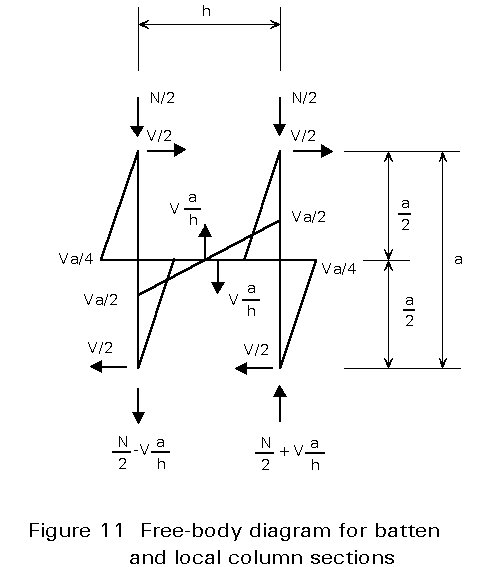
The battens, their connections to the chords, and the chords themselves are checked for the moments and forces due to the shearing force V and the axial force N as shown in Figure 11.

The design philosophy of Eurocode 3 [1] may be summarized in the following six steps:

derive the design axial load.
derive the flexural stiffness and the shear stiffness of the built-up columns.
derive the elastic critical load of the built-up column.
compute the design bending moment at midspan and the design shear force at the ends of the built-up-column.
check the buckling strength of the chords at midspan.
check the strength of the web members and of their connections to the chords for the most loaded panel at the ends.

6. CONCLUDING SUMMARY

The bearing capacity of built-up columns is largely affected by the shear deformations.
It is possible to study the behaviour of built-up columns using a simple elastic model.
Because of shear deformations the initial lack of straightness of the column is strongly amplified.
The design method proposed in Eurocode 3 is based on the above approach.

7. REFERENCES

[1] Eurocode 3: "Design of Steel Structures": ENV 1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.

[2] Ballio, G. & Mazzolani, F. M., "Theory and Design of Steel Structures", Chapmann and Hall, New York, 1983.

8. ADDITIONAL READING

Bleich, F., "Buckling Strength of Metal Structures", McGraw Hill, New York, 1952.
Timoshenko, S., "Theory of Elastic Stability", McGraw Hill, New York, 1936.
Galambos, Th. V., "Guide to Stability Design Criteria for Metal Structures - Fourth Edition", J. Wiley & Sons, New York, 1988.

Table 1 Example of the influence of shear flexibility on stability