ESDEP WG 15A
STRUCTURAL SYSTEMS: OFFSHORE
To introduce the types of loads for which a fixed steel offshore structure must be designed. To present briefly the loads generated by environmental factors.
A basic knowledge of structural analysis for static and dynamic loadings.
The categories of load for which a pile supported steel offshore platform must be designed are introduced and then the different types of environmental loads are presented. The loads include: wind, wave, current, earthquake, ice and snow, temperature, sea bed movement, marine growth and tide generated loads. Loads due to wind, waves and earthquake are discussed in more detail together with their idealizations for the various types of analyses. Frequent references are made to the codes of practice recommended by the American Petroleum Institute, Det Norske Veritas, the British Standards Institution and the British Department of Energy, as well as to the relevant regulations of the Norwegian Petroleum Directorate.
The loads for which an offshore structure must be designed can be classified into the following categories:
Whilst the design of buildings onshore is usually influenced mainly by the permanent and operating loads, the design of offshore structures is dominated by environmental loads, especially waves, and the loads arising in the various stages of construction and installation. This lecture deals with environmental loads, whilst the other loadings are treated in Lecture 15A.3.
In civil engineering, earthquakes are normally regarded as accidental loads (see Eurocode 8 [1]), but in offshore engineering they are treated as environmental loads. This practice is followed in the two lectures dealing with loads, Lectures 15A.2 and 15A.3.
Environmental loads are those caused by environmental phenomena such as wind, waves, current, tides, earthquakes, temperature, ice, sea bed movement, and marine growth. Their characteristic parameters, defining design load values, are determined in special studies on the basis of available data. According to US and Norwegian regulations (or codes of practice), the mean recurrence interval for the corresponding design event must be 100 years, while according to the British rules it should be 50 years or greater. Details of design criteria, simplifying assumptions, required data, etc., can be found in the regulations and codes of practice listed in [1] - [8].
Wind loads act on the portion of a platform above the water level, as well as on any equipment, housing, derrick, etc. located on the deck. An important parameter pertaining to wind data is the time interval over which wind speeds are averaged. For averaging intervals less than one minute, wind speeds are classified as gusts. For averaging intervals of one minute or longer they are classified as sustained wind speeds.
The wind velocity profile may be taken from API-RP2A [2]:
Vh/VH = (h/H)1/n (1)
where:
Vh is the wind velocity at height h,
VH is the wind velocity at reference height H, typically 10m above mean water level,
1/n is 1/13 to 1/7, depending on the sea state, the distance from land and the averaging time interval. It is approximately equal to 1/13 for gusts and 1/8 for sustained winds in the open ocean.
From the design wind velocity V(m/s), the static wind force Fw(N) acting perpendicular to an exposed area A(m2) can be computed as follows:
Fw = (1/2) r V2 Cs A (2)
where:
r
is the wind density (r » 1.225 Kg/m3)Cs is the shape coefficient (Cs = 1,5 for beams and sides of buildings, Cs = 0,5 for cylindrical sections and Cs = 1,0 for total projected area of platform).
Shielding and solidity effects can be accounted for, in the judgement of the designer, using appropriate coefficients.
For combination with wave loads, the DNV [4] and DOE-OG [7] rules recommend the most unfavourable of the following two loadings:
a. 1-minute sustained wind speeds combined with extreme waves.
b. 3-second gusts.
API-RP2A [2] distinguishes between global and local wind load effects. For the first case it gives guideline values of mean 1-hour average wind speeds to be combined with extreme waves and current. For the second case it gives values of extreme wind speeds to be used without regard to waves.
Wind loads are generally taken as static. When, however, the ratio of height to the least horizontal dimension of the wind exposed object (or structure) is greater than 5, then this object (or structure) could be wind sensitive. API-RP2A requires the dynamic effects of the wind to be taken into account in this case and the flow induced cyclic wind loads due to vortex shedding must be investigated.
The wave loading of an offshore structure is usually the most important of all environmental loadings for which the structure must be designed. The forces on the structure are caused by the motion of the water due to the waves which are generated by the action of the wind on the surface of the sea. Determination of these forces requires the solution of two separate, though interrelated problems. The first is the sea state computed using an idealisation of the wave surface profile and the wave kinematics given by an appropriate wave theory. The second is the computation of the wave forces on individual members and on the total structure, from the fluid motion.
Two different analysis concepts are used:
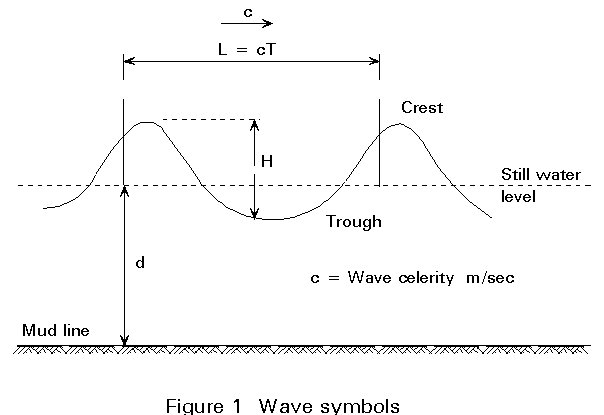
Wave theories describe the kinematics of waves of water on the basis of potential theory. In particular, they serve to calculate the particle velocities and accelerations and the dynamic pressure as functions of the surface elevation of the waves. The waves are assumed to be long-crested, i.e. they can be described by a two-dimensional flow field, and are characterized by the parameters: wave height (H), period (T) and water depth (d) as shown in Figure 1.

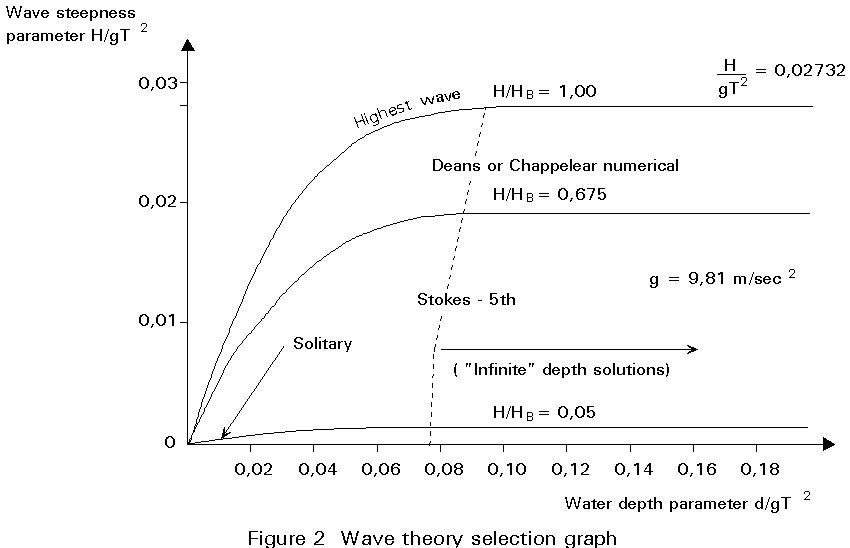
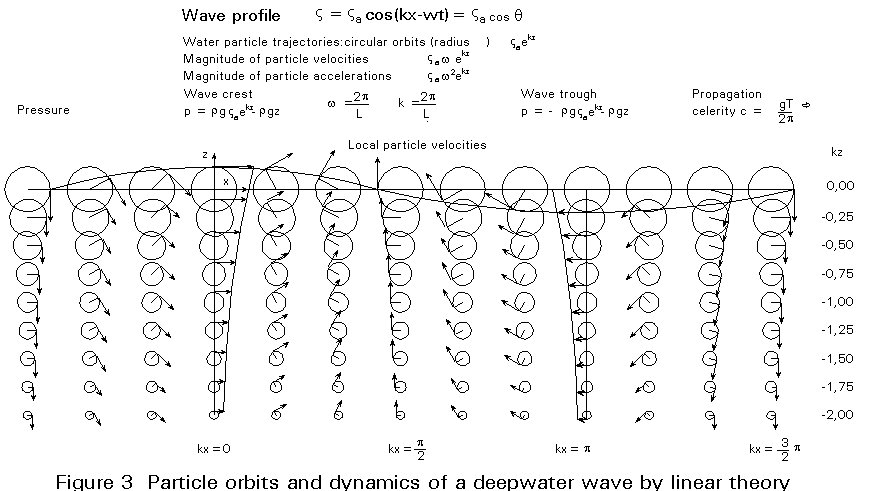
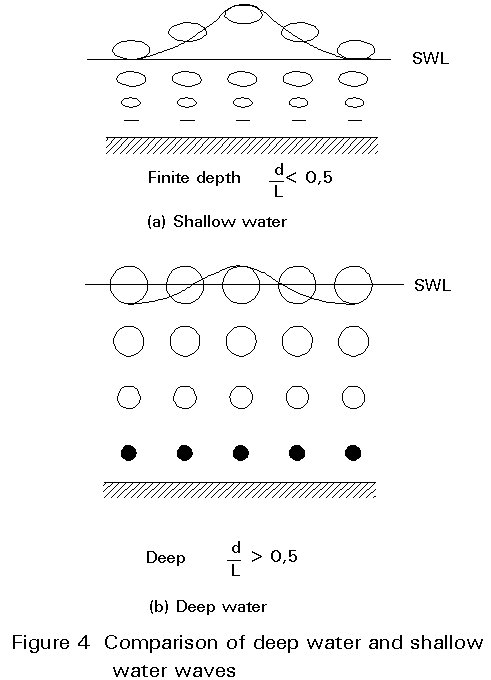
Different wave theories of varying complexity, developed on the basis of simplifying assumptions, are appropriate for different ranges of the wave parameters. Among the most common theories are: the linear Airy theory, the Stokes fifth-order theory, the solitary wave theory, the cnoidal theory, Dean's stream function theory and the numerical theory by Chappelear. For the selection of the most appropriate theory, the graph shown in Figure 2 may be consulted. As an example, Table 1 presents results of the linear wave theory for finite depth and deep water conditions. Corresponding particle paths are illustrated in Figures 3 and 4. Note the strong influence of the water depth on the wave kinematics. Results from high-order wave theories can be found in the literature, e.g. see [9].
In reality waves do not occur as regular waves, but as irregular sea states. The irregular appearance results from the linear superposition of an infinite number of regular waves with varying frequency (Figure 5). The best means to describe a random sea state is using the wave energy density spectrum S(f), usually called the wave spectrum for simplicity. It is formulated as a function of the wave frequency f using the parameters: significant wave height Hs (i.e. the mean of the highest third of all waves present in a wave train) and mean wave period (zero-upcrossing period) To. As an additional parameter the spectral width can be taken into account.
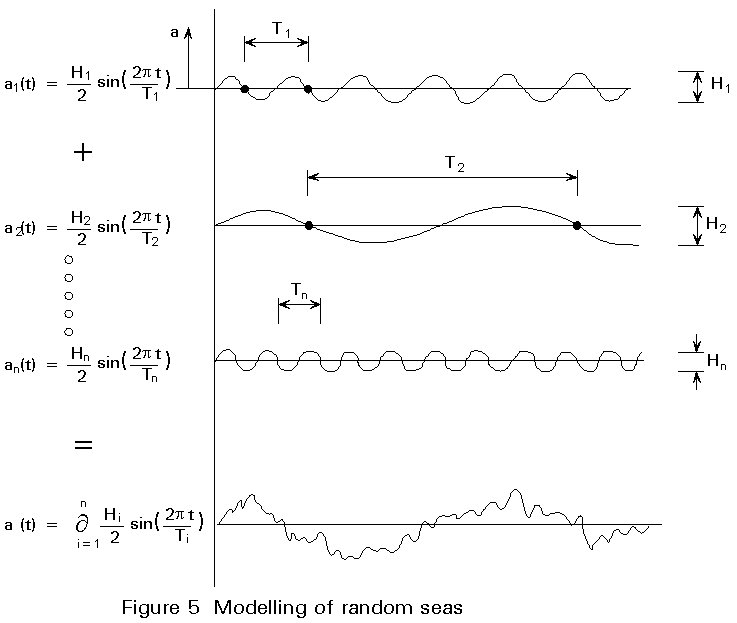
Wave directionality can be introduced by means of a directional spreading function D(f,s), where s is the angle of the wave approach direction (Figure 6). A directional wave spectrum S (f,s) can then be defined as:
S (f,s ) = S(f).D (f,s ) (3)
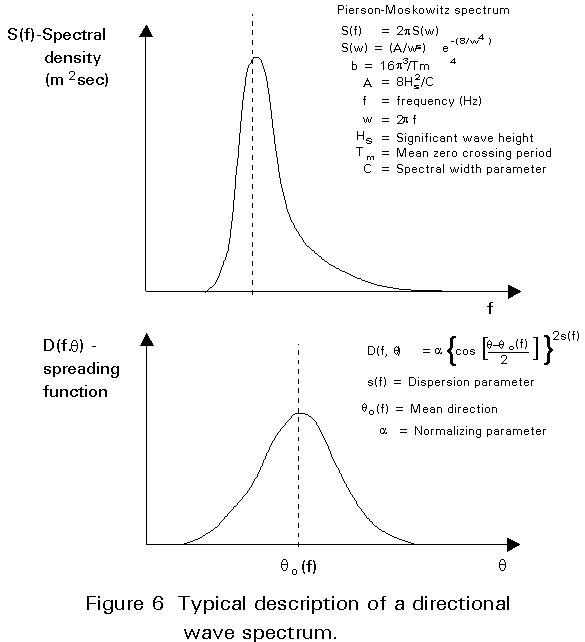
The response of the structure, i.e. forces, motions, is calculated by multiplication of the wave energy spectrum with the square of a linear transfer function. From the resulting response spectrum the significant and the maximum expected response in a given time interval can be easily deduced.
For long-term statistics, a wave scatter diagram for the location of the structure is needed. It can be obtained from measurements over a long period or be deduced from weather observations in the region (the so-called hindcast method). The scatter diagram contains the joint probability of occurrence of pairs of significant wave height and mean wave period. For every pair of parameters the wave spectrum is calculated by a standard formula, e.g. Pierson-Moskowitz (Figure 6), yielding finally the desired response spectrum. For fatigue analysis the total number and amplitude of load cycles during the life-time of the structure can be derived in this way. For structures with substantial dynamic response to the wave excitation, the maximum forces and motions have to be calculated by statistical methods or a time-domain analysis.
Structures exposed to waves experience substantial forces much higher than wind loadings. The forces result from the dynamic pressure and the water particle motions. Two different cases can be distinguished:
The steel jackets of offshore structures can usually be regarded as hydrodynamically transparent. The wave forces on the submerged members can therefore be calculated by Morison's equation, which expresses the wave force as the sum of an inertia force proportional to the particle acceleration and a non-linear drag force proportional to the square of the particle velocity:
![]() (4)
(4)
where
F is the wave force per unit length on a circular cylinder (N)
v, |v| are water particle velocity normal to the cylinder, calculated with the selected wave theory at the cylinder axis (m/s)
are water particle acceleration normal to the cylinder, calculated with the selected wave theory at the cylinder axis (m/s2)
r
is the water density (kg/m3)D is the member diameter, including marine growth (m)
CD, CM are drag and inertia coefficients, respectively.
In this form the equation is valid for fixed tubular cylinders. For the analysis of the motion response of a structure it has to be modified to account for the motion of the cylinder [10]. The values of CD and CM depend on the wave theory used, surface roughness and the flow parameters. According to API-RP2A, CD » 0,6 to 1,2 and CM » 1,3 to 2,0. Additional information can be found in the DNV rules [4].
The total wave force on each member is obtained by numerical integration over the length of the member. The fluid velocities and accelerations at the integration points are found by direct application of the selected wave theory.
According to Morison's equation the drag force is non-linear. This non-linear formulation is used in the design wave concept. However, for the determination of a transfer function needed for frequency domain calculations, the drag force has to be linearized in a suitable way [9]. Thus, frequency domain solutions are appropriate for fatigue life calculations, for which the forces due to the operational level waves are dominated by the linear inertia term. The nonlinear formulation and hence time domain solutions are required for dynamic analyses of deepwater structures under extreme, storm waves, for which the drag portion of the force is the dominant part [10].
In addition to the forces given by Morison's equation, the lift forces FD and the slamming forces FS, typically neglected in global response computations, can be important for local member design. For a member section of unit length, these forces can be estimated as follows:
FL = (1/2) r CL Dv2 (5)
FS = (1/2) r Cs Dv2 (6)
where CL, CS are the lift and slamming coefficients respectively, and the rest of the symbols are as defined in Morison's equation. Lift forces are perpendicular to the member axis and the fluid velocity v and are related to the vortex shedding frequency. Slamming forces acting on the underside of horizontal members near the mean water level are impulsive and nearly vertical. Lift forces can be estimated by taking CL » 1,3 CD. For tubular members Cs » p.
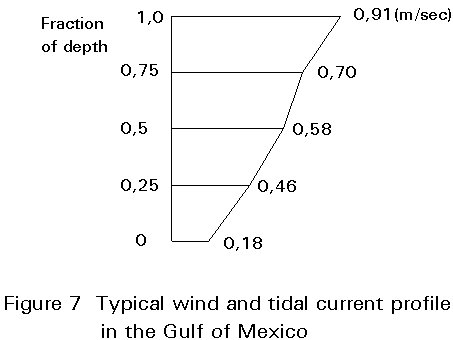
There are tidal, circulation and storm generated currents. Figure 7 shows a wind and tidal current profile typical of the Gulf of Mexico. When insufficient field measurements are available, current velocities may be obtained from various sources, e.g. Appendix A of DNV [4]. In platform design, the effects of current superimposed on waves are taken into account by adding the corresponding fluid velocities vectorially. Since the drag force varies with the square of the velocity, this addition can greatly increase the forces on a platform. For slender members, cyclic loads induced by vortex shedding may also be important and should be examined.
Offshore structures in seismic regions are typically designed for two levels of earthquake intensity: the strength level and the ductility level earthquake. For the strength level earthquake, defined as having a "reasonable likelihood of not being exceeded during the platform's life" (mean recurrence interval ~ 200 - 500 years), the structure is designed to respond elastically. For the ductility level earthquake, defined as close to the "maximum credible earthquake" at the site, the structure is designed for inelastic response and to have adequate reserve strength to avoid collapse.
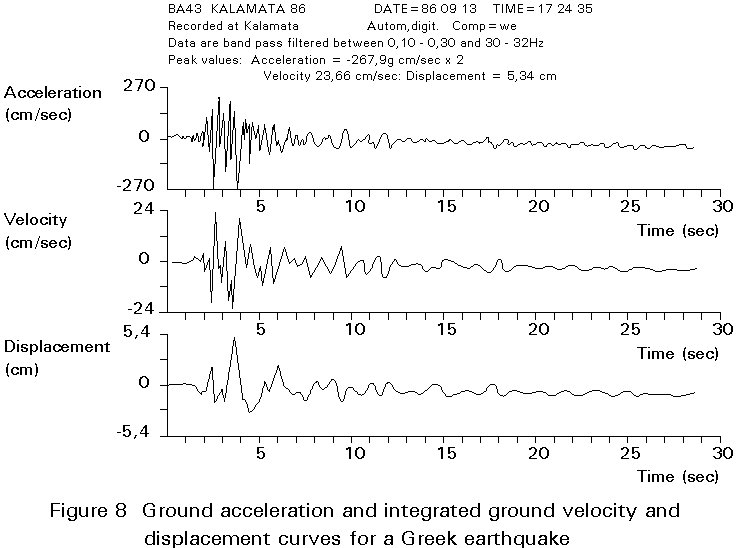
For strength level design, the seismic loading may be specified either by sets of accelerograms (Figure 8) or by means of design response spectra (Figure 9). Use of design spectra has a number of advantages over time history solutions (base acceleration input). For this reason design response spectra are the preferable approach for strength level designs. If the design spectral intensity, characteristic of the seismic hazard at the site, is denoted by amax, then API-RP2A recommends using amax for the two principal horizontal directions and 0,5amax for the vertical direction. The DNV rules, on the other hand, recommend amax and 0,7 amax for the two horizontal directions (two different combinations) and 0,5 amax for the vertical. The value of amax and often the spectral shapes are determined by site specific seismological studies.
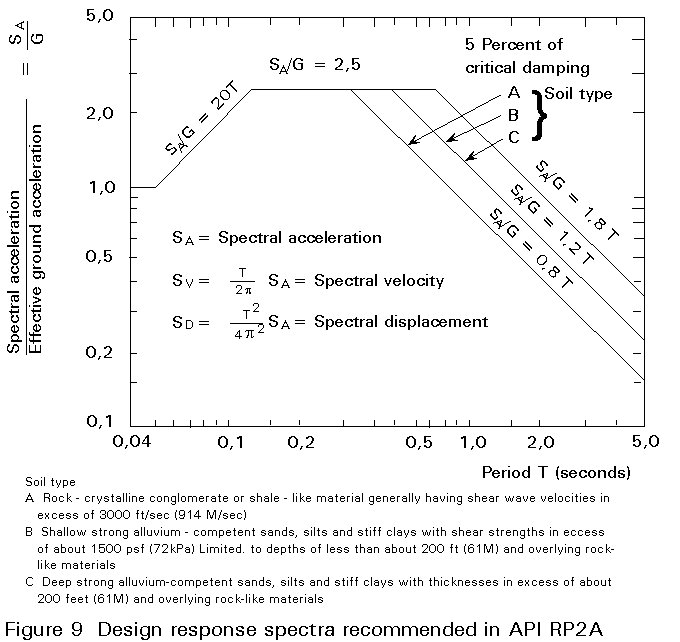
Designs for ductility level earthquakes will normally require inelastic analyses for which the seismic input must be specified by sets of 3-component accelerograms, real or artificial, representative of the extreme ground motions that could shake the platform site. The characteristics of such motions, however, may still be prescribed by means of design spectra, which are usually the result of a site specific seismotectonic study. More detail of the analysis of earthquakes is given in the Lectures 17: Seismic Design.
Ice is a primary problem for marine structures in the arctic and sub-arctic zones. Ice formation and expansion can generate large pressures that give rise to horizontal as well as vertical forces. In addition, large blocks of ice driven by current, winds and waves with speeds that can approach 0,5 to 1,0 m/s, may hit the structure and produce impact loads.
As a first approximation, statically applied, horizontal ice forces may be estimated as follows:
Fi = CifcA (7)
where:
A is the exposed area of structure,
fc is the compressive strength of ice,
Ci is the coefficient accounting for shape, rate of load application and other factors, with usual values between 0,3 and 0,7.
Generally, detailed studies based on field measurements, laboratory tests and analytical work are required to develop reliable design ice forces for a given geographical location.
In addition to these forces, ice formation and snow accumulations increase gravity and wind loads, the latter by increasing areas exposed to the action of wind. More detailed information on snow loads may be found in Eurocode 1 [8].
Offshore structures can be subjected to temperature gradients which produce thermal stresses. To take account of such stresses, extreme values of sea and air temperatures which are likely to occur during the life of the structure must be estimated. Relevant data for the North Sea are given in BS6235 [6]. In addition to the environmental sources, human factors can also generate thermal loads, e.g. through accidental release of cryogenic material, which must be taken into account in design as accidental loads. The temperature of the oil and gas produced must also be considered.
Marine growth is accumulated on submerged members. Its main effect is to increase the wave forces on the members by increasing not only exposed areas and volumes, but also the drag coefficient due to higher surface roughness. In addition, it increases the unit mass of the member, resulting in higher gravity loads and in lower member frequencies. Depending upon geographic location, the thickness of marine growth can reach 0,3m or more. It is accounted for in design through appropriate increases in the diameters and masses of the submerged members.
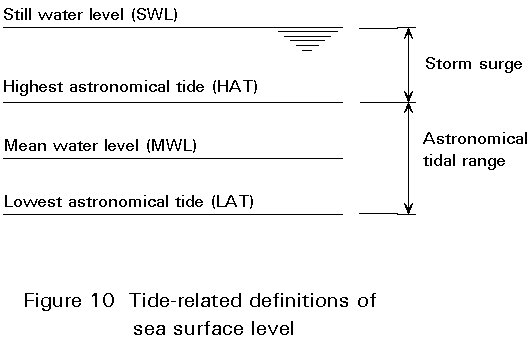
Tides affect the wave and current loads indirectly, i.e. through the variation of the level of the sea surface. The tides are classified as: (a) astronomical tides - caused essentially from the gravitational pull of the moon and the sun and (b) storm surges - caused by the combined action of wind and barometric pressure differentials during a storm. The combined effect of the two types of tide is called the storm tide. Tide dependent water levels and the associated definitions, as used in platform design, are shown in Figure 10. The astronomical tide range depends on the geographic location and the phase of the moon. Its maximum, the spring tide, occurs at new moon. The range varies from centimetres to several metres and may be obtained from special maps. Storm surges depend upon the return period considered and their range is on the order of 1,0 to 3,0m. When designing a platform, extreme storm waves are superimposed on the still water level (see Figure 10), while for design considerations such as levels for boat landing places, barge fenders, upper limits of marine growth, etc., the daily variations of the astronomical tide are used.
Movement of the sea floor can occur as a result of active geologic processes, storm wave pressures, earthquakes, pressure reduction in the producing reservoir, etc. The loads generated by such movements affect, not only the design of the piles, but the jacket as well. Such forces are determined by special geotechnical studies and investigations.
[1] Eurocode 8: "Structures in Seismic Regions - Design", CEN (in preparation).
[2] API-RP2A, "Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms", American Petroleum Institute, Washington, D.C., 18th ed., 1989.
[3] OCS, "Requirements for Verifying the Structural Integrity of OCS Platforms"., United States Geologic Survey, National Centre, Reston, Virginia, 1980.
[4] DNV, "Rules for the Design, Construction and Inspection of Offshore Structures", Det Norske Veritas, Oslo, 1977 (with corrections 1982).
[5] NPD, "Regulation for Structural Design of Load-bearing Structures Intended for Exploitation of Petroleum Resources", Norwegian Petroleum Directorate, 1985.
[6] BS6235, "Code of Practice for Fixed Offshore Structures", British Standards Institution, London, 1982.
[7] DOE-OG, "Offshore Installation: Guidance on Design and Construction", U.K., Dept. of Energy, London 1985.
[8] Eurocode 1: "Basis of Design and Actions on Structures", CEN (in preparation).
[9] Clauss, G. T. et al: "Offshore Structures, Vol 1 - Conceptual Design and Hydromechanics", Springer, London 1992.
[10] Anagnostopoulos, S.A., "Dynamic Response of Offshore Structures to Extreme Waves including Fluid - Structure Interaction", Engr. Structures, Vol. 4, pp.179-185, 1982.
[11] Hsu, H.T., "Applied Offshore Structural Engineering", Gulf Publishing Co., Houston, 1981.
[12] Graff, W.J., "Introduction to Offshore Structures", Gulf Publishing Co., Houston, 1981.
[13] Gerwick, B.C. Jr., "Construction of Offshore Structures", John Wiley, New York, 1986.
Table 1 Results of Linear Airy Theory [11]
Phase q = kx - w t Relative water depth d/L |
Deep water d/L ³ 0,5 |
Finite water depth d/L < 0,5 |
Velocity potential q
Surface elevation z Dynamic pressure pdyn = |
za cos q r gza ekz cos q |
za cos q
|
|
Water particle velocities
horizontal u =
vertical w = |
za w ekz cos q
za w ekz sin q |
|
|
Water particle accelerations horizontal u' = vertical w' = |
za w2 ekz sin q
-za w2 ekz cos q |
|
Wave celerity c = Group velocity cgr = Circular frequency w
= Wave length L = Wave number k = |
co = cgr = w
= Lo = ko = |
c = cgr = w
= L = kd tanh kd = |
|
Water particle displacements horizontal x vertical z
Particle trajectories |
-za ekz sin q za ekz cos q
Circular orbits |
Elliptical orbits |
Where
z a =