Previous | Next | Contents

Lecture 14.9: Methods of Analysis for

Multi-Storey Frames

OBJECTIVE/SCOPE

To present the factors which are taken into account in the analysis of multi-storey buildings, and the methods which can be adopted.

PRE-REQUISITES

Lecture 1B.3: Background to Loadings

Lectures 1B.7: Introduction to Design of Multi-Storey Buildings

Lectures 5: Computer Aided Design and Manufacture

RELATED LECTURES

Lecture 14.7: Anatomy of Multi-Storey Buildings

Lecture 14.10: Simple Braced Non-Sway Multi-Storey Buildings

Lecture 14.13: Design of Multi-Storey Frames with Partial Strength & Semi-Rigid Connections

Lecture 14.15: Tall Building Design

SUMMARY

Methods of analysing the elements of structure described in Lecture 14.7 are presented.

The following aspects are considered:

• Purpose of Analysis
• Performance Requirements
• Loading Effects
• Analysis Assumptions
• Hand Methods
• Computer Methods
• Future Systems

1. INTRODUCTION

Lecture 14.7 described the assembly of the structural elements forming the anatomy of multi-storey buildings. This lecture examines the procedures which should be adopted to conduct an analysis of the structure. It should be noted that specific methods of analysis for certain types of frames (e.g. rigid jointed, wind-moment, braced and partial strength) are, for clarity, presented in the appropriate subsequent lectures. The objective of this particular lecture is therefore to introduce the general philosophy of frame analysis and to identify those considerations which are common to all frame types.

2. OBJECTIVES AND PRELIMINARY CONSIDERATIONS

The objectives of analysis are:

• To gain a better understanding of the structural behaviour under the action of the applied loading.
• To obtain sets of applied actions which are in equilibrium with the reactions and which can be used for the design of individual structural elements.
• To predict the static and dynamic movements of the structure and their effect on the building finishes and occupant comfort.

In order determine whether the structure is satisfactory, the structural response is compared with the appropriate codified limits, e.g. member stresses, local and overall deflection response, stability criteria, etc.

Clearly it is important that the model assumed in the analysis is indeed representative of the way in which the proposed structure would behave. As a result, it is important that prior to conducting an analysis, consideration is given to the following:

• An appraisal of the building construction. For example, the type of floor construction and its ability to distribute lateral forces, or the nature of the cladding and how it will distribute the applied wind loading.
• The overall building geometry and proposed foundation construction. For large structures, expansion joints may be required thereby disrupting the overall integrity of the structure.
• For structures with top storeys at different levels, and hence significantly different load intensities over the 'footprint', the potential for ground settlement due to soil-structure interaction or the eventual need for structural articulation should be considered in the analysis (Figure 1).
• It is particularly important that the load path through the structure is identified, i.e. how the permanent and variable actions are transferred to the primary structural frame and how these actions are subsequently transferred by the frame to the foundations (Figure 2).
• The nature and magnitude of the permanent and variable actions and the co-existent combinations which are likely to have the most detrimental effects on the structure.
• An understanding of building economy including fabrication and erection procedures. Specifically, the ideal arrangement of the primary structural frame and whether the nature of the frame, e.g. simple or rigid beam to column connections, is appropriate for the structure being considered.
• Overall frame stability and ability to resist lateral forces. Specifically, whether bracings are present within the structure or whether lateral forces have to be resisted by frame action.

3. ACTIONS

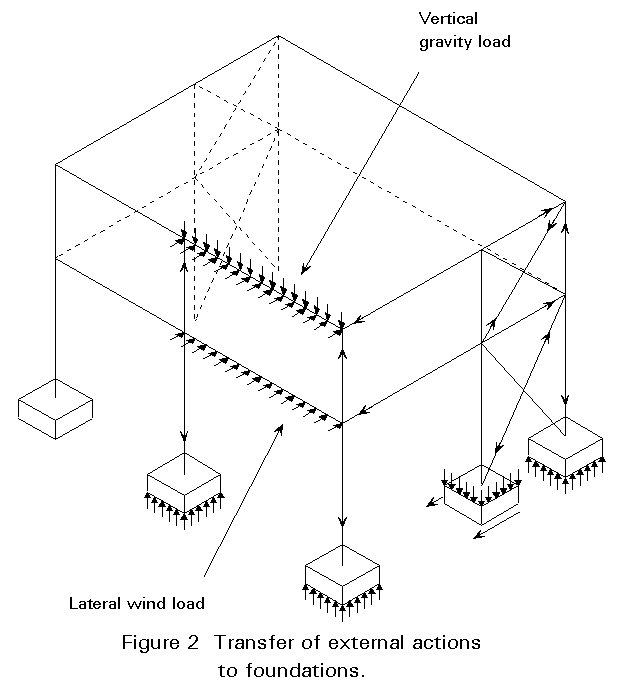
The following categories of loading are considered for the analysis of multi-storey buildings:

3.1 Permanent Actions

These actions typically comprise the following:

• Self-weight of structural elements (slabs, beams, columns, bracing).
• Floor finishes.
• False ceiling.
• Services.
• Fixed partitions.
• Fire protection.
• Cladding.

Information on the characteristic load for proprietary products can be obtained from manufacturer's literature.

3.2 Variable Actions - Imposed Load

Minimum imposed loading is based on the usage of the building being considered, and specified in local regulations. Buildings are often designed for imposed loads specified in excess of these minima, to increase the flexibility of future usage. Items to consider are:

• People.
• Furniture.
• Moveable partitions.
• Plant.
• Storage.
• Snow/roof loading.

Usually only static analysis is required for imposed load, but dynamic analysis may be necessary to assess the effects of:

• Seismic actions.
• Vehicle impact.
• Transmission of noise and vibrations from plant within the building or from adjacent roads or railways.
• Floor vibrations due to walking, usually assessed by considering the effect of a standard 'heel drop'.

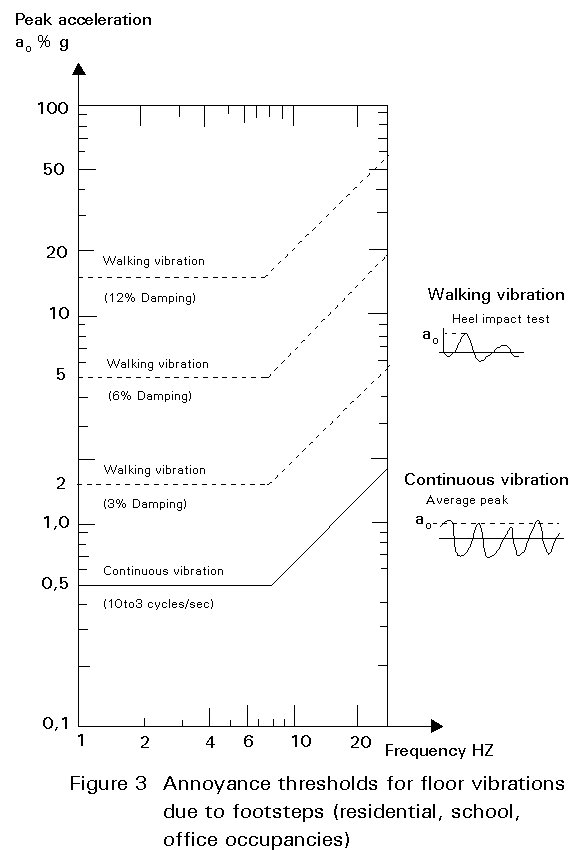
Figure 3 presents generally accepted limits (annoyance thresholds) for vibrations induced by walking.

3.3 Variable actions - Wind Loads

The magnitude of the design wind loading to be applied to a building depends on the location and local topography of the site. The following terms are used to describe the different types of wind loading:

• Mean: Static effect due to steady wind flow around the building. Usually based on windspeed averaged over a period of one hour. The magnitude decreases with increase in ground roughness upwind of the site.
• Gust: Dynamic effect of gusts on the building. The magnitude of this component reduces as building size increases since an individual gust is not large enough to envelop the whole of a large building. Magnitude increases with ground roughness.
• Resonant: Dynamic effect due to the flexibility of the building interacting with the applied gusts. Magnitude increases with building height, and reduces with mass and damping.

Cross-wind effects may also be present:

• List: Static and dynamic 'aerofoil' effect due to building shape.
• Buffeting: Dynamic effect due to fluctuations in wind direction.
• Vortexes: Dynamic effect of vortices being shed on alternate sides downwind of the building.

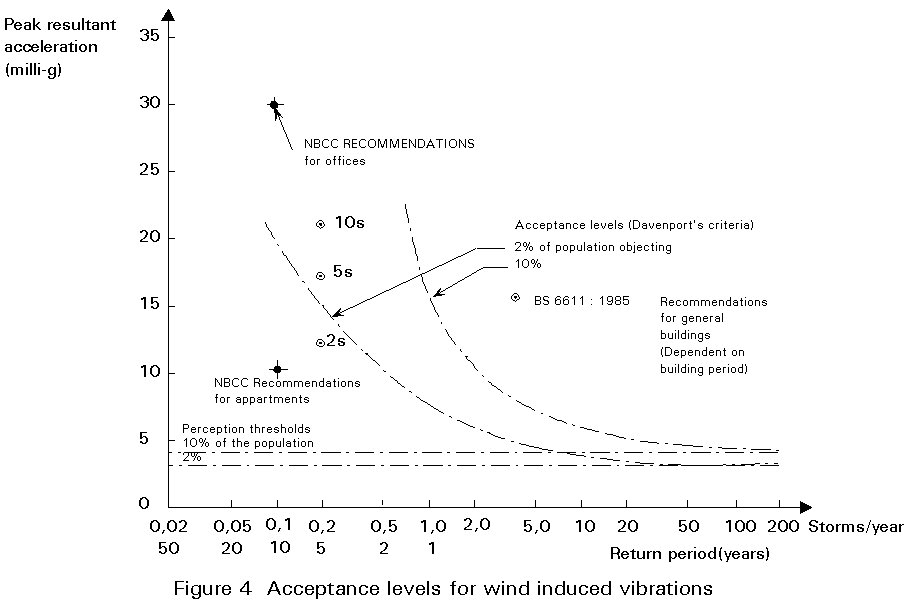
For low and medium rise multi-storey buildings, complex wind analysis is usually unnecessary, and equivalent static loads defined in local regulations or Eurocode 1 (when available) may be used. Cross-wind effects are not normally significant for ultimate limit state analysis, but can have an important influence on comfort. Figure 4 presents some acceptance levels for wind induced vibrations.

3.4 Seismic Actions

Seismic action need normally not be considered in northern Europe, but is the dominating action in southern Europe. It is a function of:

• Regional seismicity.
• Local ground conditions.
• Building period (a function of height, mass and lateral stiffness).
• Structural form and materials.

Buildings subjected to seismic forces should be designed not only for strength but also for ductility. Details for the seismic resistant design are given in Lectures 17.

3.5 Temperature

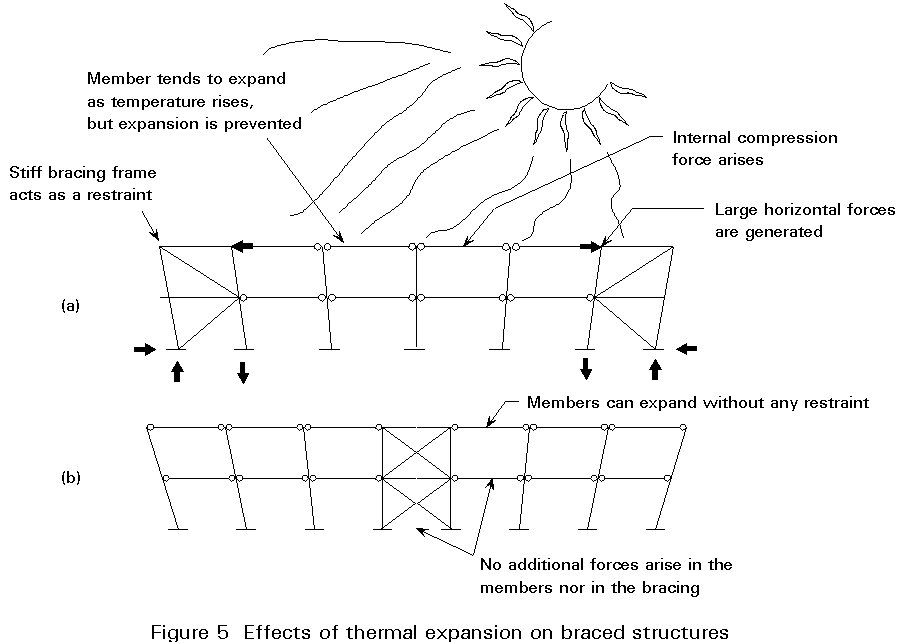
Depending on the size and layout of the structure, thermal strains due to change in temperature can be significant. For example, if a long building has stiff bracing frames at each end, differential thermal strains will be generated between the superstructure and the foundations and large internal forces will be generated in beams and bracings (Figure 5a). To avoid this inconvenience, the location of bracings in the middle of the structure allows for free expansion of members without any restraint (Figure 5b), so no additional internal forces arise.

Thermal effects can be taken into account by adopting an appropriate temperature range (depending on the building location and usage) and a thermal coefficient of expansion for steel.

4. LIMIT STATES

The structure should be analysed to ensure that the probability of reaching any of the limit states at which it would become unfit for its intended use within the design life of the building is acceptably low.

4.1 Ultimate Limit State

The ultimate limit state considers the strength and stability requirements of the structure - essentially a collapse criterion. Individual types of characteristic loadings are multiplied by the relevant factors to derive the design loads, and applied in the most unfavourable realistic combination for the element or overall structural response being considered. A simplified expression when considering only the most unfavourable variable action is of the following form:

F_d =

where

F_d is the design action

G_k is the characteristic permanent load

Q_k is the characteristic variable load

g_G is the permanent load factor

g_Q is the variable load factor

The load factors proposed in Eurocode 3 [1] when designing for the ultimate limit state are given in Table 1. It should be noted that permanent actions are effectively the self weight of the elements of the structure and of non-structural elements, whilst variable actions are the applied loads, e.g. wind load, imposed floor load, settlement load, etc. Where more than one variable actions are considered to act co-existently, the load factors are reduced to reflect the reduced probability of this combination of loading actually occurring on the real structure, i.e.:

F_d =

Figure 6 shows how these load factors may be applied to determine the most critical design conditions for a range of different frame types. The allowance for imperfections is explained in Section 6.

4.2 Serviceability Limit State

The serviceability limit state for steelwork addresses the following:

• deformations or deflections which adversely affect the appearance or the effective use of the structure (including the proper functioning of machines or services).
• vibration, oscillation or sway which causes discomfort to the occupants of a building or damage to its contents.
• deformations, deflections, vibrations, oscillations or sway which causes damage to finishes or non-structural elements.

Eurocode 3 [1] presents guidelines to ensure that these limits are not exceeded.

When assessing the serviceability performance of the structure subject to a single variable load in addition to the permanent (self weight) load, the load factors are unity. The structure is effectively analysed using the characteristic actions. However, where the serviceability response of the structure is being assessed with more than one variable action, or where the dynamic response is being considered, Eurocode 3 [1] introduces three types of combinations of loading:

• Rare combination

• Frequent combination

• Quasi-permanent combination

The factors in the above formula (y_o, y₁ and y₂ ) vary and are detailed in the individual National Application Documents for Eurocode 3 of the various Member States. The rare combination, as the name suggests, considers a larger proportion of the variable action compared to that assumed in the frequent combination. It is a requirement in Eurocode 3 that the rare combination of loading is considered when conducting an appraisal of the member or overall frame deflections, whereas the frequent combination of load is considered when the dynamic response of the structure is being assessed.

5. FRAME CLASSIFICATION

When analysing a principle structural frame, it is important to classify it as being either sway or non-sway, braced or unbraced. The classification of the frame determines the method of global analysis which may be employed and the influence of secondary effects on frame actions (see Lecture 14.8).

5.1 Classification as Braced or Unbraced

The frame is classified as braced or unbraced depending on the relative stiffness of the bracing system providing the resistance to lateral forces.

The criterion for a braced frame is that the bracing system is at least five times stiffer than the lateral stiffness of the frame. It should be noted that this requirement will automatically be satisfied for simple frames incorporating bracing systems. In the absence of a bracing system a simple frame has zero lateral stiffness.

For a frame which is deemed to be braced, the bracing system must be designed to resist all lateral loads applied to the structure including those arising due to frame imperfections, see Section 6.

A frame which is classified as braced is automatically designed as non-sway. A frame which is deemed to be unbraced must be further classified as either sway or non-sway.

5.2 Classification as Sway or Non-Sway

A frame is classified as non-sway for a given load case if the following criterion is satisfied:

where

V_sd is the design value of the total vertical load

V_cr is the elastic critical load for failure of the frame in a sway mode.

For multi-storey beam-and-column plane frames, with beams connecting each column at each storey level, classification as non-sway can be made for a given load combination, simply by determining whether the following condition is satisfied:

where

d is the deflection over a storey height (interstorey drift)

h is the storey height

V is the vertical reaction at the bottom of a storey

H is the horizontal reaction at the bottom of a storey.

Frames classified as sway must subsequently be checked for overall sway stability using the procedures given in Eurocode 3 [1].

6. ALLOWANCE FOR IMPERFECTIONS

The effects of frame imperfections must be included in the global analysis of any frame. Effectively, the imperfections are treated as a load case to be used in conjunction with all the critical load combinations acting on the frame.

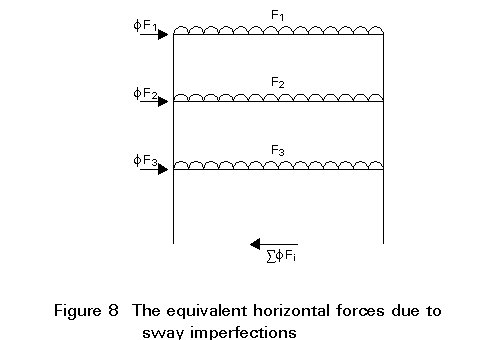
In Eurocode 3 [1], imperfection effects are quantified in terms of an initial sway rotation at the base of the column (see Figure 7), but may then be converted to an equivalent horizontal force (see Figure 8).

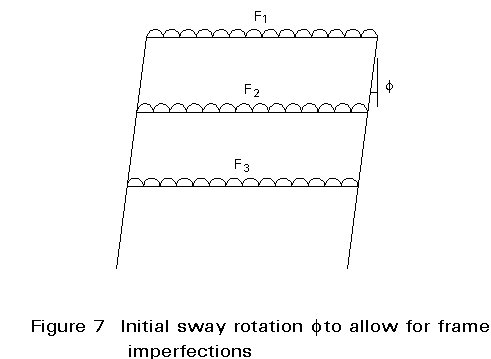
The initial sway imperfections f may be determined directly from Table 3. The number of columns n_c includes only the main load bearing columns (i.e. only those which carry over 50% of the average load taken by all the columns in the frame being considered) which extend through all the storeys considered when evaluating n_s. Similarly, the number of storeys n_s only includes those floor and roof levels which are connected to all the columns included in evaluating n_c. A single value of f is adopted for the whole frame. If the column arrangement is such that it is possible to calculate more than one value, it is permissible to choose the value which has the most beneficial effect. Alternatively, any other choice will be conservative. The values of f range from an upper bound of 1/200 to a lower limit of about 1/630.

The equivalent horizontal force fF at each roof and floor level is calculated by multiplying the proportion of the vertical load, F, applied at that level by the initial sway imperfection, f (see Figure 8).

The equivalent horizontal forces may be applied in any horizontal direction, but only in one direction at a time.

At the supports, the equivalent horizontal forces obtained by multiplying the vertical reactions by f are applied so that the equivalent horizontal forces on the whole frame form a closed system, which results in a net horizontal reaction of zero in the absence of actual horizontal loads.

It should be emphasised that the resulting equivalent horizontal forces should be applied in addition to any other horizontal forces which may be acting.

7. ANALYSIS MODEL AND METHOD

The modelling of structural systems will be covered in Annex H in a future addendum to Eurocode 3 [2]. In the meantime the following general principles apply.

It is conventional to assume that the members in a principle structural frame have centre lines intersecting at a point. The manner in which the design actions are distributed around the frame is dependant on the nature of the connections and the measures employed to resist lateral loading. Table 3, extracted from Eurocode 3, illustrates the different methods of global analysis which are permitted depending on the type of framing and connection.

7.1 Simple Framing

The method for analysis and design of simple framing is dealt with at length in Lecture 14.10. The frame incorporates a separate bracing system which is designed to resist lateral loading and provide lateral stability to the part of the structure resisting gravity load (see Figure 9).

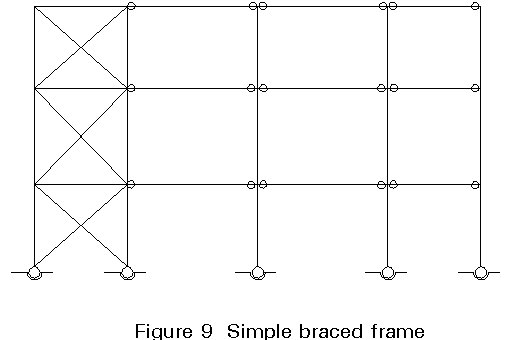
The model assumes the following:

• The members intersecting at a joint are pin connected.
• The necessary flexibility in connections may result in some non-elastic deformation of the connecting parts (other than the fasteners).
• The supporting columns are not subjected to any direct moment transferred through the connection.

As a result, the structure is statically determinate. The internal forces and moments are therefore determined from a consideration of statics.

Simple frames are invariably designed as non-sway (see Section 5) and, as a result, the effect of frame deformations on the distribution of internal forces and moments can be ignored.

7.2 Continuous Frames

Such structures are statically indeterminate. A detailed appraisal of the analysis and design of partial-strength (or partially continuous) frames is presented in Lecture 14.13, whilst those where full continuity is assumed at the connection are addressed in Lecture 14.14.

For continuous frames, the internal forces can be determined using either:

a. elastic global analysis.

b. plastic global analysis.

Whilst elastic methods of global analysis can be used throughout, plastic global analysis is only applicable where the frame members are of the appropriate classification to enable the development of plastic hinges.

7.2.1 Elastic first order analysis

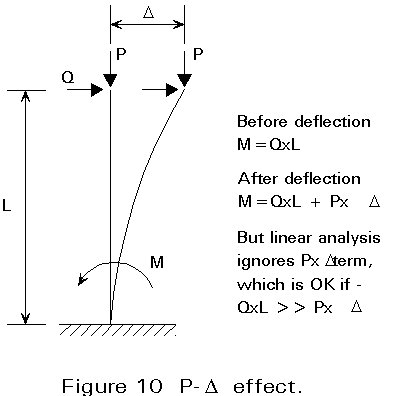
In a first-order analysis, the additional secondary actions due to the deformation of the structure (see Figure 10) are ignored. 

This assumption is only valid in the following cases:

a. Where the frame is classified as braced (see Section 5.1).

b. Where the frame is classified as non-sway (see Section 5.2).

c. Where a design method is used in which an indirect allowance (amplification) is made for the occurrence of second-order effects.

In this latter case, the sway moments obtained from a first order linear elastic analysis are multiplied by the ratio:

(Formula 1)     1/[1 - V_sd/V_cr],         for     V_sd/V_cr £ 0,25

where

V_sd is the design value of the total vertical load.

V_cr is the elastic critical value in a sway mode.

For conventional framed structures, the ratio V_sd/V_cr can be determined as follows:

The first order elastic method of analysis is a convenient approach. Most design offices possess computer software capable of performing this method of analysis on large highly indeterminate structures. Figures 11 - 13 show typical graphical output from first order analysis made using computer software.

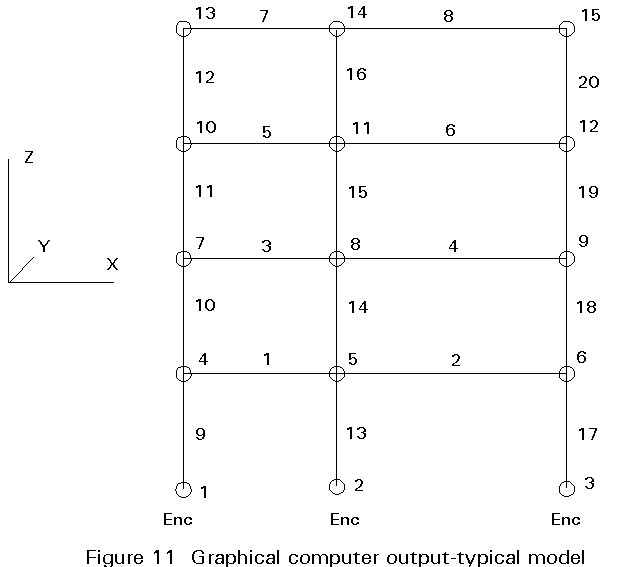
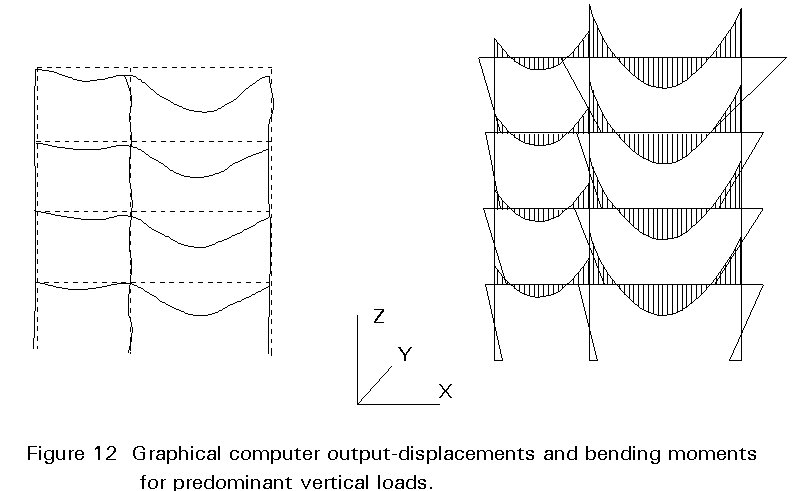
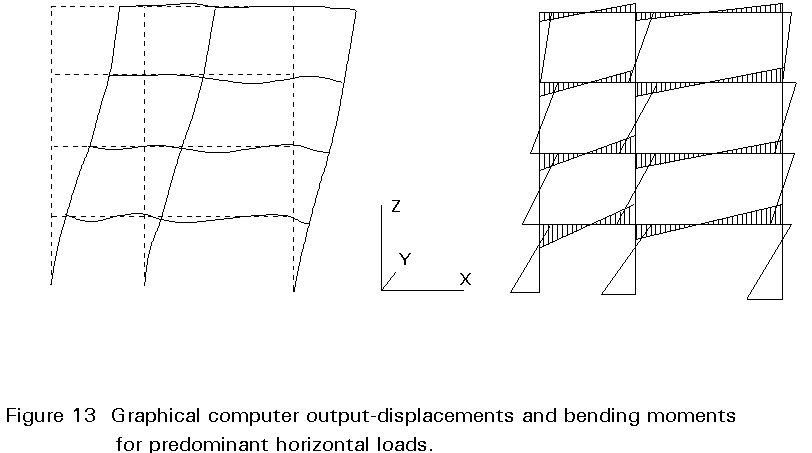
As an alternative, hand calculations can be performed on appropriate subframes within the structure (see Figure 14) comprising a significantly reduced number of members. These simple calculations are also recommended to make some physical check of the out-put of the computer.

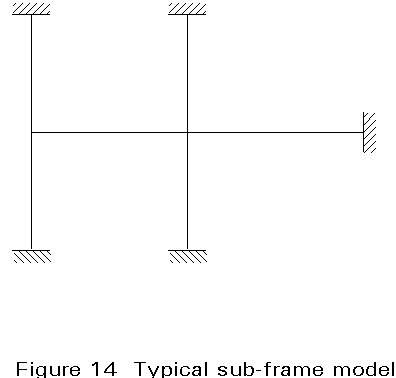
When conducting the analysis of an isolated subframe it is important that:

a. The subframe is indeed representative of the structure as a whole.

b. The selected boundary conditions are appropriate.

c. Account is taken of the possible adverse effects between adjacent subframes.

7.2.2 Plastic global analysis

Plastic global analysis may be made by means of either:

• Rigid-plastic, methods (i.e. simple plastic) or
• Elastic-plastic methods.

Elastic-plastic methods require quite sophisticated computer programs, which enable second order effects to be taken into account.

As a design tool, Eurocode 3 [1] does present a method of rigid plastic analysis which takes into account secondary effects by amplifying the design internal forces and moments by means of the ratio given in Formula (1). The method is only applicable where frames have fixed bases and the only hinge to form in the column is at the base (see Figure 15) and the V_Sd/V_cr ratio does not exceed 0,2.

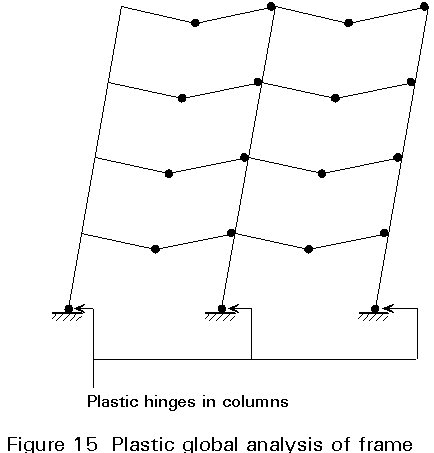
By means of this method the design is based on an incomplete mechanism in which the columns are designed to remain elastic at the calculated plastic hinge moment.

For building structures in which the required rotations are not calculated, all members containing plastic hinges shall have Class 1 cross-sections at the plastic hinge location.

8. CONCLUDING SUMMARY

• The main objectives of the analysis of multi-storey buildings have been identified.
• The various loadings have been given and the limit states for verification have been discussed.
• Analytical models and methods relevant to the frame characteristics have been presented.

9. REFERENCES

[1] Eurocode 3: "Design of Steel Structures": ENV1993-1-1: Part 1.1: General rules and rules for buildings, CEN, 1992.

[2] Eurocode 3: "Design of Steel Structures": Annex H: Modelling of Building Structures for Analysis (in preparation).

	Permanent actions (gG)	Variable actions (gQ)
		Leading variable action	Accompanying variable actions
Favourable effect gF,inf	1,0*)	0,0	0,0
Unfavourable effect gF,sup	1,35*)	1,5	1,5

Table 1: Load factors in Eurocode 3

Type of framing	Method of global analysis	Types of connections
Simple	Pin joints	Nominally pinned Nominally pinned
Continuous	Elastic	Rigid Nominally pinned (6.4.3.1)
	Rigid-Plastic	Full-strength Nominally pinned
	Elastic-Plastic	Full-strength Rigid Nominally pinned
Semi-continuous	Elastic	Semi-rigid Rigid Nominally pinned
	Rigid-Plastic	Partial-strength Full-strength Nominally pinned
	Elastic-Plastic	Partial-strength Semi-rigid Partial-strength Rigid Full-strength Semi-rigid Full-strength Rigid Nominally pinned

Table 2: Methods of global analysis given in Eurocode 3 for different types of frame and connection

nc ns	2	3	4	5	6	7	8
1	1/200	1/220	1/230	1/240	1/245	1/250	1/255
2	1/240	1/260	1/275	1/285	1/290	1/295	1/300
3	1/275	1/300	1/315	1/325	1/335	1/345	1/375
4	1/300	1/325	1/345	1/355	1/365	1/375	1/400
5	1/315	1/350	1/365	1/375	1/385	1/400	1/400
6	1/325	1/360	1/375	1/390	1/400	1/400	1/400
ns is the number of storeys nc is the number of columns per plane f = kc ks f0 with f0 = 1/200 kc = √{0,5 + 1/nc} ≤ 1 ks = √{0,2 + 1/nc} ≤ 1

Table 3: Sway imperfection f

Previous | Next | Contents