ESDEP WG 15C
STRUCTURAL SYSTEMS: MISCELLANEOUS
To outline calculation methods for guyed masts, in particular manual calculation of erection tensions in guy ropes, and computer calculation of forces in non-linear mode; to explain the main principles of non-linear calculation; to cover erection methods.
Lecture 15C.3: Lattice Towers and Masts
The components of a guyed mast are described, i.e. mast, guy ropes, accessories, equipment.
Specific items of the calculation of guyed masts are introduced. The definition and manual calculation of erection tensions in guy ropes is described together with the principles and computer calculation of forces and strains.
The fabrication and erection of guyed masts are briefly discussed.
The permanent development of regional, national and international communications requires very high structures.
These structures are generally designed for the following purposes:
Steel guyed masts may be designed specifically to meet the above needs since very high structures (up to 600 metres high) which are both light and stiff can be designed and built in steel.
The present lecture does not give:
The component parts of a guyed mast are:
It is not the purpose of the present lecture to describe the foundations in a detailed way. It is only indicated that:
The mast may be considered as a continuous beam on elastic supports which are provided by the guy ropes. In most cases, it is a lattice column with a square or equilateral triangle cross-section. It is also possible to design masts with a round tubular section.
For the masts with 3 faces, the most adequate section of the legs is a round hollow section or a round solid section. A circular flange is welded onto each end of each leg element. The leg elements are connected by bolting the flanges one to the other. The truss bars are bolted onto gusset plates which are welded on the legs. The section of the truss bars consists of one or two connected angles or of a circular tube. Where circular tubes are used, they are slotted and pressed at their ends in order to allow the bolted connection.
For masts with 4 faces, the same design can be used as for masts with 3 faces. Single angle legs or two cross-connected angle legs can also be used.
Where angle legs are used, the leg elements are connected together with bolted cover-plates. The truss bars are bolted onto the legs, either directly or by bolted gusset plates. For this type of mast, there is no welding work.
A mast structure with 4 faces must have horizontal bracings which prevent deformation of the cross-section.
In general in the few cases where the mast has a round tubular section, the mast has a fixed foot. It is very difficult to make a pinned foot for a mast with a tubular section. The mast elements are connected together by welded hollow flanges with external bolts.
The guy ropes create elastic bearings with horizontal action on the mast. Where the mast has three truss faces, each bearing consists of three guy ropes situated in the medium plane of the angle of two adjacent truss faces. Where the mast has four truss faces, each bearing consists of four guy ropes each situated in a diagonal plane. Where the mast has a round hollow section, each bearing has three 120° spaced guy ropes or four 90° spaced guy ropes.
All the guy ropes (3 or 4) of a bearing form the same angle with the horizontal plane of between 30° and 60° .
The guy ropes are generally steel cables. In special cases where a guy rope enters the transmission field, cables of synthetic materials can be used. The three or four guy ropes which constitute a bearing must be of the same material.
The criteria for choosing cables are as follows:
It is always necessary to find the best compromise between the two first criteria and the fifth. The above analysis generally leads to the use of all-steel cables with large diameter wires, mainly one twist cables.
Guy ropes are provided with a socket at each end. The sockets are cast steel pieces of a conical shape and two parallel flanges which receive a connecting pin. The cable is entered in the hollow conical part of the socket, the wires constituting the cable are separated and bent to form a regular "flower" which is introduced into the socket. The socket cavity is then filled with a molten alloy. At one of the cable ends, the pin perpendicular to cable connects the bottom socket to the foundation anchor. At the other end, the pin connects the top socket to a thick gusset plate welded onto the mast leg.
The structural accessories are generally supplied by the steel manufacturer of the mast and include:
The equipment is generally not supplied by the steel manufacturer of the mast and includes:
The design of guyed masts - as other structures - contains two main steps:
In this step, the engineer chooses a first set of sections for the bar elements which constitute the mast and for the different guy ropes in relation to the overall design requirements:
and also in relation to the loads to be considered, i.e.
The difficulty of this step arises from the interdependence of the values of the actions and of the choice of the sections. The procedure can be as follows:
a. Choose the first set of sections for bar elements of the mast by considering the mast as a continuous beam on unmovable supports (at guy rope connection levels). This beam supports the actions of the self-weight and of the maximum wind. In this step, the dynamic factor on wind actions can be evaluated with a first vibration mode period (in seconds) equal to a hundredth of the height of the mast (in metres).
The engineer must provide the sections with a large margin in expectation of phenomena which have not been considered explicitly, i.e.
× the compression in the mast due to the guy rope tensions.
× the influence on the bending moment diagram of the misalignment of the supports in the real deformed structure.
× the influence on the bending moment diagram of the eccentricity of the guy rope compression in the mast.
× the effects of the non-linear behaviour of the structure. These effects are explained in Section 3.2.
× the yielding of foundations in tension and compression.
It is not possible to state a definite percentage for the margin which should be provided because it depends on the overall design of each guyed mast.
b. Calculate the actions of the mast on its supports, according to the simplified procedure. Fi is the action of the mast on the support i, Tij is the unknown tension of the guy rope i.j when the maximum wind blows (j varies from 1 to 3 or from 1 to 4 following the number of ropes per support); ai is the angle between rope and support i; i is at a horizontal plane.
c. In the case of a support i with three guy ropes, if the wind blows in the direction of the guy rope i.1, then:
Ti.2 = Ti.3
(Ti.1 - Ti.2) = Fi / cos ai
The section of the ropes which constitute the support i is chosen so that:
Ti.1 - Ti.2 £ 0,75
where
TR.i is the breaking force of the rope
s is the required safety factor.
d. In the case of a support i with four guy ropes , if the wind blows in the direction of the guy rope i.1, then:
(Ti.1 - Ti.3) = Fi / cos ai
The section of the ropes which constitute the support i is chosen so that:
Ti.1 - Ti.3 £ 0,75 
e. After the choice of the guy rope sections, the engineer has to determine the values of initial tensions Ti.o (the same value for a given i and any j) which are necessary to keep the supports aligned when the maximum wind blows. The general slope of the mast for which initial tensions are calculated is chosen in relation to the supported equipment.
In this step, the following approximations are made:
× the direct action of wind on the guy ropes is neglected
× the effect of the temperature is neglected
× the second order effects due to mast compression are neglected
× the deformed shape of the rope i.j is considered as a parabola, the length of which is:
si.j = li.j + 
where li.j is the chord length
fi.j =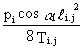 
is the maximum cable deformation, measured perpendicularly to the chord.
pi is the weight per metre of the cable.
If Di.j is the projection, on the vertical plane which contains the rope i.j, of the horizontal displacement Di of the support i:
Di.j
= 
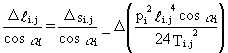
Di.j
= 
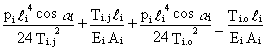
at the first order, where li is the initial value of the chord length. The above equation can be written in the form:
Di.j = g (Ti.j) - g (Ti.o)
f. Where the support i has 3 ropes and when the wind blows in the direction of the rope i.1:
Di.j = Di = - 2 Di.2 = - 2 Di.3
The equations may be solved as follows: A graph of the function g (Ti.1) is drawn, point by point for different values of Ti.1 together with a separate graph of the function - 2 g (Ti.2) at the same scale on transparent paper. If the two graphs are superimposed in order to get simultaneously:
Ti.1 - Ti.2 = 0,75 
(distance between the curves on the T scale)
g(Ti.1) + 2 g (Ti.2) = 2 Di (distance between the curves on the g (T) scale)
then Ti.o is read at the intersection of the two curves, on the T scale.
g. Where the support i has 4 ropes, the same procedure is applied:
Di.1 = Di = - Di.3
and the curves g (Ti.1) and - g (Ti.3) are drawn as above.
After the sections of the mast bar elements and the guy ropes, and the values of the initial tensions have been evaluated, the final dimensioning step can begin.
The final values of forces and strains are calculated by computer.
It is necessary to use software which allows:
The first non-linear factor is that the stiffness of a guy rope is not constant. The stiffness varies with the tension. It is necessary therefore to have a cable element in the finite element library of the software. The stiffness matrix of the cable element contains terms which depend on the strain status of the element (geometric stiffness terms). A cable element is defined by the origin and extremity nodes, its length and its loading.
The second non-linear factor is that the displacements are generally not infinitely small so that the bar elements have to be described by a stiffness matrix, the terms of which depend on the displacement status (deformed stiffness terms).
It is not necessary to take into consideration the geometric stiffness terms of the bar elements if the calculation model contains a sufficient number of nodes (at least 5 nodes between two supports).
The calculation runs in which the above mentioned factors are taken into account are iterative ones and are executed independently for each loading combination. In the first step, the displacements are calculated with a cable stiffness corresponding to the initial tension and a bar element stiffness corresponding to nil displacements. The forces are calculated from the displacements.
In the second step, the stiffness matrix terms are modified in relation to the displacements and forces previously obtained. A new set of displacements and forces is calculated. The difference between the second step forces and the first step ones gives the equilibrium residuals. The forces and displacements due to the equilibrium residuals are calculated, using the second step stiffness matrix and added to those calculated at the first step.
The process continues until the residuals become negligible. The structure has then reached the deformed equilibrium status which corresponds to the considered loading combination.
The successive runs are generally:
To do that, a preliminary calculation model is used where the cable elements have the length of their chord in the unloaded status and where the anchoring node of each guy rope is free to displace along the chord. At the anchoring node of each cable, an external force equal to the initial tension is applied. The equilibrium length of a cable element is equal to the chord length plus the calculated displacement of the anchoring node.
In the calculation model, the mast can be described in a detailed way (legs and truss bars) or in a global way (co-linear equivalent bars). In the global description, the influence of shear deformations is taken into account and also the eccentricity of the connections of the guy rope from the centre line of the mast.
The usual checks which norms and codes prescribe for steel structures have to be done from the results of the calculations mentioned in Section 3.2. They contain the following points in particular:
× the mast foot
× the reinforcement around apertures
× the guy rope connection rings.
The current dimensions of the conical cavity of sockets to get a correct connection are:
diameter of the large part: 2,5 times the cable diameter
diameter of the narrow part: 1,15 times the cable diameter
height of the cavity: 5 times the cable diameter.
After the cable has been entered through the narrow part, it is bound for a distance of 5 diameters from the former. The wires are separated and bent over about 10 wire diameters in order to form a "flower" as regular as possible, the large diameter of which is about 2,5 times the cable diameter. The "flower" is entered in the socket. The socket is heated to about 200° C and then fulfilled with a molten alloy (electrolytic zinc or Pb - Zn - Sb alloy).
The bottom part of the mast, e.g. four sections of about 6 metres each, is assembled at ground level and erected with a crane. This part is supported in its vertical position by temporary guy ropes, the tension of which has been calculated in the erection study.
An erection device is connected at the top of the erected part. It is used to lift the following section, either in one piece or face by face, or bar by bar, into position.
After the connection of the new mast section, the erection device is transferred to the 'new' top of the assembled part.
This operation is repeated section by section and the provisional guy ropes are placed as determined by the erection study.
When the level of the first permanent guy ropes is reached, they are mounted and their tension is adjusted to the calculated initial tension. The temporary guy ropes of the bottom part are removed.
After all the mast sections and permanent guy ropes have been assembled, the final adjustment of the tensions is made in order to ensure that:
The tension adjustment is made with a large diameter threaded bar which is placed between the bottom sock of the rope and the anchoring device through pins and flanges. The bar is aligned with the cables.
For the adjustment, the threaded bar is shunted by two parallel jacks.
The current tolerances for verticality are given by:
D = 
cm for h ³ 20m