GRAVIMETRIJA

1 Naloga gravimetrije

Gravimetrija pomeni merjenje težnosti. Izhaja iz latinske besede "gravis" – težek in grške besede "metrew" – meriti. Gravimetrija predstavlja skupino metod uporabne geofizike, ki se ukvarjajo z merjenjem težnega pospeška in s proučevanjem težnostnega polja. Rezultati gravimetrične izmere imajo velik pomen za geodezijo oz. ožje gledano fizikalno geodezijo, satelitsko geodezijo itd., vsaj se vse geodetske meritve opravljajo v težnostnem polju. Na primer nehorizontirani instrument pomeni neupoštevanje vpliva težnosti na opravljene meritve. Brez poznavanja celostne teorije težnostnega polja Zemlje je tudi naše geodetsko znanje nepopolno.

Težni pospešek, ki ga določamo z gravimetričnimi meritvami je velikost (jakost) vektorja sile teže. Ta predstavlja rezultanto delovanja centrifugalno in gravitacijske (privlačne) sile na točko obravnave (točko v kateri izvajamo gravimetrične meritve). Velikost vektorja sile teže – težnost ima fizikalno dimenzijo pospeška. V praksi (posebej geodetski in geofizikalni) je lažje delati s skalarjem, zato se namesto sile, obravnava pospešek. S tem v zvezi je bil uveden pojem težnega pospeška (uporablja se tudi težnostni pospešek).

Enota za težni pospešek v SI sistemu merskih enot je ms^-2. Za prikaz odstopanj težnosti od polja normalne sile teže se uporabljata manjši enoti:

1mms^-2=10^-6ms^-2 1nms^-2=10^-9ms^-2

V geodeziji in geofiziki oz. gravimetriji je še vedno v rabi pomožna enota:

1mGal=10^-5ms^-2 1mGal=10^-8ms^-2

Izpeljani sta iz enote Gal, poimenovani po G. Galileu (1Gal=1cms^-2, CGS sistem merskih enot). Te enote v uradni rabi niso dovoljene, vendar se v znanstvenem komuniciranju še vedno uporabljajo. V tabeli so podane zveze med enotami SI sistema in enotami v praktični rabi.

količina	SI enote	uporabniške (tradicionalne)
težnost	10^-2 ms^-2	1 Gal
(težni pospešek)	10^-5 ms^-2	1 mGal
	10^-8 ms^-2	1 mGal
težnostni potencial	10 m^2s^-2 =	1 kGal
	= 1 g.p.u.

Tabela 1: merske enote za težni pospešek v gravimetriji

Zaradi sploščenosti Zemlje na polih, sprememb v gostoti Zemljine notranjosti in zaradi različnega centrifugalnega pospeška se vrednost g giblje med g=9,78ms^-2 (na ekvatorju) in g=9,83ms^-2 (na polih). Srednja vrednost težnega pospeška na površini Zemlje znaša g=9,803 ms^-2.

Pri izvajanju gravimetričnih meritev je pomembno poznati tudi položaj opazovališča, saj se težni pospešek spreminja na površini Zemlje. Spremembe nastajajo zaradi že omenjene sploščenosti Zemlje na polih in zaradi Zemljine nehomogene strukture (spememb gostote kamnin v njeni notranjosti).

Naloga gravimetrije je določitev težnostnega polja Zemlje (lahko tudi drugih nebesnih tečes) kot funkcijo položaja in časa z merjenjem težnega pospeška in gradienta težnosti (vektor, ki kaže v smeri največjega naraščanja težnosti).

Gradient težnega pospeška je pomemben pri določitvi sprememb težnega pospeška po enoti dolžine. Uporablja se za vrednostenje in interpretacijo podatkov gravimetrične izmere. Horizontalni gradient težnega pospeška lahko merimo s pomočjo gradiometra ali pa torzijske tehtnice. Osnovna enota gradienta težnega pospeška je Eötvös (E):

1E = 1´10^-9s^-2 = 1mms^-2/km = 0,1mgal/km

2 Metode merjenja težnega pospeška

Čeprav so številni fizikalni pojavi odvisni od vrednosti težnega pospeška, lahko izkoristimo samo nekatere od njih za njegovo določitev. Vse obstoječe metode merjenja lahko razdelimo na dinamične in statične.

1. Dinamične metode obravnavajo gibanje telesa pod vplivom sile teže. Pri njih merimo neposredno čas, ki potrebuje telo, da se premakne iz enega v drugi položaj.

2. Statične metode obravnavajo spremembo ravnovesja telesa pod vplivom sile teže in njej nasprotne sile. Neposredno merimo dolžinski premik ali spremembo kota telesa konstantne mase. Nasprotno delujoča sila je v tem primeru lahko sila prožnosti vzmeti, torzija nitke, membrane itd.

Instrumente za merjenje težnega pospeška imenujemo gravimetri. Ne glede na to, katero metodo uporabljamo, določamo lahko absolutne in relativne vrednosti težnega pospeška. Absolutne meritve pomenijo določitev težnega pospeška v polnem iznosu, relativne meritve pa nam dajo razlike vrednosti težnega pospeška med dvema točkama (glede na točko z znano vrednostjo g-ja).

Z dinamičnimi metodami lahko določamo absolutne in relativne vrednosti težnega pospeška. Pri absolutnih določitvah vrednosti g je potrebno izmeriti poleg časa, še razdaljo (dolžino nihala, oz. dolžino poti prostega padanja).

S statičnimi metodami določamo samo relativne vrednosti težnega pospeška, torej razlike vrednosti težnega pospeška med dvema točkama.

2.1 Absolutne meritve težnega pospeška

Pri dinamičnih metodah merjenja težnega pospeška izkoriščamo naslednja fizikalna pojava:

· nihanje telesa pod vplivom sile teže,

· prosti pad telesa.

Absolutni gravimetri za dinamične metode so konstruirani kot nihala ali pa t.i. balistični instrumenti (gravimetri na principu prostega padanja telesa v vakuumu). Danes se skoraj izključno uporabljajo gravimetri na principu prostega padanja. Natančnost absolutne določitve vrednosti težnega pospeška s prostim padom znaša od ±10^-7 do ±10^-9 g.

Meritve z nihalom so bile, vse do sredine tega stoletja, prevladujoči način določitve absolutnih vrednosti težnega pospeška. Princip delovanja teh gravimetrov je zasnovan na teoriji matematičnega nihala oz. nihanja togega telesa (težno nihalo).

Gravimetri z nihalom so grajeni na principu težnega nihala (togo telo, ki niha pod vplivom težnosti) ali pa t.i. reverzibilnega nihala (ima dve osi nihanja, dve vrtišči).

Instrumente na principu matematičnega nihala lahko zasledimo že na začetku XVIII. stoletja. Natančnost takratne določitve težnosti v pariški astronomski observatoriji je znašal okrog
±10^-5g. XIX. stoletje je zaznamovano z konstrukcijo lažjih prenosnih nihalnih instrumentov, ki so svoj vrhunec doživeli v začetku tega stoletja.

Problem absolutne določitve težnega pospeška z nihalnimi gravimetri je od samega začetka vezan na pravilno ovrednotenje vpliva številnih pogreškov. Če želimo določiti g z natančnostjo ±10^-7g=0,1mGal z nihalom dolžine 1m in nihajnim časom 1s, je potrebno poznati njegovo dolžino z natančnostjo ±0,1mm in izmeriti nihajni čas z natančnostjo ±0,1ms. Te natančnosti pa lahko dosežemo samo s posebnimi napravami: merjenje dolžin s pomočjo laserskih interferometrov in merjenje časa s elektronskimi števci, ki jih krmilijo časovni signali. Z upoštevanjem vsega naštetega je zgornja meja določitve absolutne vrednosti g ±0,3-0,4mGal (reverzibilna nihala). Natančnost z začetka stoletja je bila desetkrat manjša.

Pozkusi za določitev absolutne vrednosti težnega pospeška na principu prostega padanja telesa so bili prvič opravljeni med leti 1950 in 1960. Možni so bili šele takrat, ko je sodobna tehnologija (metrologija) omogočila merjenje dolžin in časa s natančnostjo ±0,5nm oz. ±0,2ns (laserski interferometri in elektronsko merjenje časa ® uvedba kvarčnih kristalov).

Matematična zasnova določitve g je merjenje časa (t) v katerem telo zaradi prostega padanja preide določeno pot (s):

od tod je

Največji vpliv na določitev g ima pogrešek izmerjene razdalje (poti) s. To pomankljivost lahko odpravimo s kombinacijo navpičnega meta in prostega pada. Posebna naprava vrže telo v višino; ko le-to doseže največjo višino začne prosto padati. Registriramo samo čas med deli poti navzgor in navzdol (1).

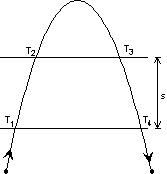
slika 1: princip merjenja časa pri balističnemu gravimetru

Časovne intervale med dvema sosednima točkama označimo z t₁=T₄–T₁ in t₂=T₃–T₂. Težni pospešek dobimo potem kot:

Od leta 1970 približno trideset različnih prenosnih absolutnih gravimetrov (na principu prostega padanja) je bilo narejenih in danih v uporabo. Instrumenti se uporabljajo za razvoj in izmero fundamentalne gravimetrične mreže točk, za pridobitev podatkov o časovnih spremembah težnostnega polja ter v različnih raziskavah na področju tektonskih premikov, volkanologije, seizmike, oceanogafije itd.

Natančnost določitve absolutne vrednosti g s prenosnimi absolutnimi gravimetri je danes 3mGal do 4mGal. Največji vpliv na natančnost ima mikroseizmičnost okolice.

2.2 Relativno merjenje težnega pospeška

Pri relativnih meritvah težnega pospeška čutilo (senzor) gravimetra omogoča posredno ali neposredno opazovanje ene od dveh temeljnih količin pospeška, časa ali dolžine. To je nedoločen problem, ki ga lahko rešimo z opazovanjem časa ali dolžine na enem opazovališču, pri čemer je druga, neopazovana količina privzeta kot fiksna. Razliko vrednosti težnega pospeška med dvema točkama lahko izračunamo iz opazovanih razlik časa ali dolžine. Relativne meritve težnosti je moč izvesti hitreje in bolj ekonomično od absolutnih meritev.

Relativne meritve težnega pospeška lahko opravimo z dinamičnimi in statičnimi metodami.

Za dinamične relativne meritve se uporabljajo gravimetri na principu nihala. Slonijo na merjenju nihajnih časov T₁ in T₂ nihala s konstantno dolžino na dveh opazovališčih.

Sistematični pogreški, ki so neodvisni od položaja in časa se izničijo v razliki pospeškov. Natančnost določitve razlike težnosti 0,1mGal terja določitev nihajnega časa nihala z relativno natančnostjo boljšo od ±5´10^-8. V praksi so se uporabljala nihala dolžine l=0,25m, s nihajnim časom T=1s; za te instrumente je zahtevana natančnost določitve časa ±0,05ms in ±0,025mm stalnosti (konstantnosti) dolžine nihala.

V prvi polovici XIX. stoletja so bile opravljene številne relativne meritve v kombinaciji z absolutnimi. Avstrijski geodet R. von Sterneck je z iznajdbo posebnega relativnega gravimetra z nihali leta 1887 omogočil množične meritve po vsej Evropi. Številne nacionalne gravimetrične mreže točk so bile izmerjene in vezane na točke z znanimi absolutnimi vrednosti g-ja. Nihalni relativni gravimetri so bili v množični uporabi do tridesetih let tega stoletja, ko so jih nadomestili t.i. mehanski gravimetri, ki omogočajo relativne meritve težnega pospeška s statičnimi metodami.

Mehanski gravimetri delujejo v biti kot izredno občutljive vzmetne tehtnice. Čutila gravimetrov predstavlja sistem vzmeti, ročic, tozijskih elementov ipd. Deformacija vzmeti nastane pod vplivom teže uteži, ki pa je odvisna od sile teže. Prirastek deformacije med dvema točkama je merilo spremembe sile teže (težnega pospeška), to pa je dejansko podatek, ki merimo.

Konstrukcijsko so izpeljani kot gravimetri z vertikalno vzmetjo ali kot gravimetri z horizontalno vzvodno (torzijsko) vzmetjo. Moderni gravimetri imajo t.i. astatičen sistem vzmeti, to je sistem, ki je nenehno uravnotežen.

Princip merjenja ponazarja v grobem naslednja slika 2. Med težo mase in napetostjo vzmeti je na danem mestu vzpostavljeno ravnotežje.

Če prestavimo gravimeter na drugo mesto, kjer je težni pospešek večji za Dg, se vzmet čutila raztegne za dolžino Dx zaradi povečanja teže za mDg. Pri tem se napetost vzmeti poveča za kDx (k je konstanta prožnosti vzmeti). Ker je povečanje teže izravnano s povečanjem napetosti, velja:

mDg = kDx

Od tod lahko izračunamo neznano razliko težnega pospeška Dg.

slika 2: princip delovanja mehanskih gravimetrov

Ob prestavitvi gravimetra na mesto z manjšo težnostjo se vzmet skrči, Dx je torej negativen.

Moderni gravimetri ne merijo premika Dx neposredno, temveč ga izničijo z nekim lažje merljivim pomikom. Najbolj znane konstrukcije sodobnih gravimetrov so naslednje: Wordenov gravimeter (kremenčeva vzmet), Scintrex gravimeter (podobna konstrukcija) in LaCoste–Rombergov gravimeter (jeklena vzmet).

Rezultati merjenja gravimetrom se izražajo v različnih enotah njegove merilne naprave (čutila). Da bi te enote lahko pretvorili v enote težnega pospeška je potrebno opraviti kalibracijo gravimetra. Kalibracija je torej postopek določevanja t.i. kalibracijske funkcije, ki omogoča omenjeno pretvorbo merskih enot. Kalibracijo lahko izvedemo na dva načina:

1. z meritvami na odprtem ® merjenjem na točkah z znanimi vrednostmi težnega pospeška,

2. z laboratorijskimi meritvami ® merjenjem sprememb težnega pospeška pri odklonu čutila gravimetra iz horizontale.

Za kalibracijo na prostem se uporabljajo gravimetrične merske baze, ki jih tvorijo točke z natančno določenimi vrednostmi težnega pospeška.

2.3 Vplivi na izmerjene vrednosti težnega pospeška

Vse vplive na izmerjene vrednosti težnega pospeška lahko razdelimo v dve skupini:

1. vplivi zaradi neizpopolnjenosti instrumenta ® instrumentalni pogreški,

2. zunanji vplivi okolice.

Instrumentalne pogreške povzroča sama konstrukcija gravimetra. V to skupino sodijo pogreški čitanja (v primeru, da gravimeter nima zaslona z možnostjo digitalnega odčitka), pogrešek zaradi nepravilnega horizontiranja, elastična histereza, nestabilna napetost v instrumentu ter kalibracijska funkcija.

Elastična histereza ali zmanšanje (popuščanje) napetosti vzmeti nastaje zaradi spremembe dolžine vzmeti s časom. Vpliv se lahko zmanjša (< 0,001mGal) z načinom dela.

Gravimeter mora biti na vsaki točki čim bolj pazljivo horizontiran. Scintrex CG-3 omogoča celo upoštevanje vpliva nehorizontalnosti na izmerjeno vrednost g-ja.

Med zunanje vplive sodijo: spremembe zunanje temperature in pritiska, vplivi magnetnega polja, pretresi gravometra zaradi transporta ter naravna in umetna mikroseizmičnost okolice.

Zaradi sprememb zunanje temperature in pritiska se spreminjajo lastnosti čutila gravimetra oz. prihaja do sprememb v ravnotežju sistema vzmeti. Zaradi tega se spreminja ničelni položaj čutila ("zero position") kar je znano kot tek (hod) gravimetra ("gravimeter drift"). S posebnim načinom dela se lahko upošteva vpliv hoda na opazovanja, predvsem v daljšem časovnem obdobju.

Natančnost relativne določitve vrednosti težnega pospeška je od 10mGal do 30mGal. Relativne meritve lahko izvajamo povsod. Navadni gravimetri se uporabljajo za meritve na kopnem in podzemeljskih prostorih in vrtinah. Za morske in zračne meritve se uporabljajo posebno prirejeni gravimetri. Natančnost teh meritev je manjša od omenjene.

3 Gravimetrična izmera

Gravimetrična izmera se med seboj loči glede na medsebojno oddaljenost izmeritvenih točk in glede na zahtevano natančnost izmere, ki jo terja sam namen nadaljnje raziskave.

Točke z izmerjenimi vrednostmi težnega pospeška so povezane v gravimetrične mreže. Te lahko razdelimo na globalne, regionalne in lokalne mreže gravimetričnih kontrolnih točk. Detajlna gravimetrična izmera za potrebe ožjih goedetskih, geoidinamičnih in geofizikalnih raziskav se potem navezuje na te mreže.

Uporaba gravimetričnih meritev v širših območjih zahteva, da gravimetrični podatki ne vsebujejo sistematičnih pogreškov. Zato se je IUGG (MZGG - Mednarodna Zveza za Geodezijo in Geofiziko) že od samega začetka prizadevala za ustanovitev referenčnega gravimetričnega sistema na katerega bi bilo možno vezati regionalne in lokalne meritve. V letih 1909 – 1971 je bil v veljavi Potsdamski težnostni sistem ("Potsdam Gravity System"). Temeljil je na absolutni določitvi vrednosti težnega pospeška na Geodetskem Inštitutu v Potsdamu leta 1900. Kasnejše meritve so ugotovile zamik v izhodišču sistema; absolutna vrednost g je večja za +14mGal.

Med leti 1950 in 1970 je bila, z mednarodnim sodelovanjem, zasnovana nova globalna gravimetrična mreža točk, ki jo je IUGG na skupščini v Moskvi leta 1971 preimenovalo v International Gravity Standardization Net 1971 I.G.S.N.71. Izhodišče novega sistema predstavlja 10 absolutnih meritev na osmih točkah. Te so določili z novo generacijo absolutnih (balističnih) gravimetrov.

Zaradi vse večjega števila razpoložljivih absolutnih gravimetrov se po letu 1983 vzpostavlja t.i. "International Absolute Gravity Basestation Network", IAGBN. Dejansko predstavlja globalno gravimetrično mrežo 0. reda. Vsebuje 36 globalno razporejenih osnovnih točk (te so kategorije natančnosti A – reda velikosti mGal ali bolje). Glavni namen te mreže je nadzor trenutnih sprememb težnosti v globalnem smislu (obstaja možnost permanentne kontrole absolutnih vrednosti na teh točkah). Poleg tega se točke uporabljajo tudi kot kontrolne točke regionalnih mrež.

Enotna evropska gravimetrična mreža 1994 ("Unified European Gravity Network 1994") - EUGN94 redstavlja poizkus vzpostavitve evropske gravimetrične mreže, ki bi z večjo natančnostjo in homogenostjo, dopolnila IGSN71. Trenutno mreža vsebuje okoli 500 točk v 11 evropskih državah. Izravnana opazovanja vsebujejo okoli 120 absolutnih in 14500 relativnih meritev. Zaradi pomanjkanja absolutnih točk v nekaterih področjih (in s tem nehomogenosti) se mreža navezuje na vrednosti IGSN71. Dosežena natančnost točk v tej mreži je okoli 20 mGal.

3.1 Gravimetrična izmera v Sloveniji

Prve grvimetrične meritve pri nas je izvedel Vojaški geografski inštitut iz Dunaja med letoma 1887 in 1894. Meritve so izvajali s Sterneckovim nihalnim gravimetrom, predvsem v dolini reke Drave, ter okolici Trsta in Reke. Namenjene so bile vojaškim potrebam. Leta 1938 je jugoslovanski VGI iz Beograda navezal osnovno gravimetrično točko v Beogradu na evropsko referenčno točko v Potsdamu.

Po drugi svetovni vojni sta bili zasnovani gravimetrični mreži I. in II. reda. Jugoslovansko mrežo I. reda je tvorilo 15 točk; v Sloveniji je točka v Ljubljani. Mreža je, razen s Parizom povezana tudi z italijansko gravimetrično mrežo. Obstaja še mreža II. reda. Konec šestdesetih let sta obe mreži združeni v eno t.i. osnovno gravimetrično mrežo Jugoslavije. Tvori jo okoli 350 točk, od tega v Sloveniji 32 točk. Razen nekaj izjem, položaji točk niso znani slovenskim strokovnjakom. Vse meritve se nanašajo na stari Potsdamski sistem in so bile opravljene z gravimetri, ki so bili kalibrirani na bazi v Jugoslaviji. Izračun vseh vrednosti težnega pospeška je bil opravljen z vrednostjo Mgala dobljenega na tej bazi (velika baza: Beograd – Skopje, mala baza: na Avali kraj Beograda).

V novo mednarodno mrežo IGSN71 sta bili vključeni, z neposrednimi meritvami, samo točki v Zagrebu in Beogradu. Primerjava vrednosti težnega pospeška na teh točkah v starem in novem sistemu poda razliko +15,1mGal; absolutna vrednost v starem sistemu je manjša. Izmerjene vrednosti g na ostalih točkah niso bile prevedene v novi sistem.

V Sloveniji obstajata tudi obsežna regionalna in lokalna izmera. Regionalna izmera je bila opravljena z namenom določitve regionalne gravimetrične karte Slovenije. Skupno število gravimetričnih točk na celem ozemlju znaša približno 2800. Lokalno oz. detajlno izmero so izvajali strokovnjaki Geološkega zavoda Ljubljana za potrebe raziskav v zvezi z nafto in plinom. Meritve so potekale od leta 1951 dalje. Popolnejši podatki obstajajo samo za obdobje 1985–1991.

Leta 1995 je GURS (Geodetska uprava Republike Slovenije) začel z delom na obnovi gravimetričnih meritev na območju Slovenije. Tako je bilo stabilizirano in opazovano šest novih absolutnih gravimetričnih točk. Te točke so: Bogenšperk, Gotenica, cerkev sv. Areha na Pohorju, Sevniški grad pri Sevnici, grad Socerb, ter grad Kluže pri Bovcu (slika 3). Meritve in izvrednotenje so opravili nemški in italijanski strokovnjaki. Te točke naj bi služile kot osnova za novo gravimetrično mrežo Slovenije.

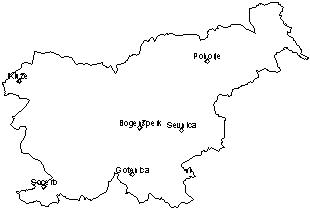
Slika 3: razporeditev absolutnih gravimetričnih točk v Sloveniji

V tabeli 2 so prikazani rezultati dosedanjih absolutnih meritev.

Točka	Absolutni Gravimeter	Epoha	Vertikalni gradient [mGal/m]	Rezultat na opazovani višini [mGal]	Opazovana višina [mm]	Standardniodklon [mGalg
Bogenšperk	FG5 101 IMGC JILAg-5	Maj 1996 Julij 1996 December 1998	-284,5 -294,7	980 593 154,3 980 593 304,9 980 593 288,4	1303 860 835	0,8
Gotenica	IMGC JILAg-5	Julij 1996 December 1998	-205,8	980 506 649,2 980 506 653,7	867 834	0,5
Pohorje	IMGC	Julij 1996		980 483 436,9	860	1,4
Sevnica	IMGC	November 1996		980 640 727,0	897	2,3
Socerb	IMGC	November 1996		980 558 272,9	895	1,3
Kluže	IMGC	November 1996		980 545 639,7	881	1,5

Tabela 2: Rezultati dosedanjih absolutnih meritev na ozemlju Slovenije

V Sloveniji se vzpostavlja tudi nova kalibracijska baza za relativne gravimetre. Baza je sestavljena iz treh absolutnih točk (Gotenica, Bogenšperk in Sevnica) in dodatne točke v Velikih Laščah. Skupni razpon baze je 134 mGal, ki jih lahko razdelimo na linije po 44,3 mGal, 42,3 mGal in 47,4 mGal. Prve relativne meritve na tej bazi so bile izvedene z instrumentoma LCR G-55 (last Finish Geodetic Institute) in Scintrex CG-3M (last GURS).