Poglavje 1. Uvod
NumPy https://numpy.org/ je odprtokodna (brezplačna) knjižnica programskega jezika Python, ki se uporablja za numerično računanje. Glavni atribut knjižnice numpy je hitrost procesiranja. In sicer je bistvo knjižnice v temu, da ne obdelujemo posameznih numeričnih vrednosti, ampak se podatke združuje v nize (eno ali več dimenzionalne sezname), ki se nato obdelujejo z integriranimi orodji.
Hitrost obdelave podatkov je, predvsem ko imamo opravka z velikim številom podatkov, za nekaj razredov velikosti večja, kot če bi uporabili čisto Python kodo. Ključ do te hitrosti se skriva v temeljih knjižnice numpy, ki poleg programskega jezika Python uporabljajo zelo hitre rutine napisane v programskem jeziku C.
V tem smislu se lahko Python v kombinaciji s knjižnico numpy uporablja kot alternativa plačljivemu programskemu jeziku Matlab https://www.mathworks.com.
|
Ta dokument je na razpolago v več različicah, in sicer kot: |
1.1. Namestitev knjižnice numpy
Knjižnico numpy lahko namestimo na več načinov; glej npr. https://numpy.org/install/.
Za začetnike oziroma za tiste, ki želijo namestiti vsa orodja za numerično obdelavo podatkov, je priporočljivo, da naložijo aplikacijo Anaconda https://www.anaconda.com/download, saj z njo dobijo čisto vsa potrebna orodja (npr. Jupyter-Notebook) in knjižnice za numerično računanje (python, numpy, scipy, matplotlib, itd.).
1.2. Uvoz knjižnice numpy
Tako kot vse ostale knjižnice tudi numpy vključimo v svojo kodo z ukazom import, kot je prikazano v spodnji programski kodi.
1
2
import numpy as np
seznam = np.array([1, 2, 3])
|
V nekaterih razdelkih smo pri opisu delovanja posameznih funkciji zaradi jedrnatosti izpustili vrstico |
| vrstica | komentar |
|---|---|
1 |
Dobra praksa je, da na začetku vsakega dokumenta vključimo potrebne knjižnice. Tu smo vključili knjižnico |
2 |
Kot primer uporabe je prikazana funkcija |
1.3. Hiter začetek
Za tiste, ki že imajo nekaj znanja iz programiranja v jeziku Python oz. izkušnje s kakšnim drugim računskim orodjem (npr. Matlab), priporočamo ogled naslednjega videa, ki v zelo zgoščeni obliki predstavi uporabo knjižnice numpy:
Poglavje 2. Numpy seznami
2.1. Ustvarjanje seznamov
Glavna prednost knjižnice numpy je v temu, da se podatke združuje v nize oziroma sezname in tako ne obdelujemo posameznih numeričnih vrednosti. Pri tem se namesto standardne podatkovne strukture list uporablja poseben seznam, ki ga uvaja knjižnica numpy. V nadaljevanju bomo temu seznamu rekli seznam numpy ali pa bolj formalno numpy.ndarray.
Seznam numpy ima podobno strukturo seznamu list iz programskega jezika Python. Glavna razlika je v tem, da je numpy.ndarray precej hitrejši in bolj učinkovit v smislu uporabljenega spomina.
2.1.1. np.array()
Seznam numpy lahko ustvarimo na več načinov. Najbolj osnoven način je, da podatkovni tip list kot argument uporabimo v funkciji np.array. Na primer:
import numpy as np seznam_list = [1, 2, 3] seznam_numpy = np.array(seznam_list)
ali pa neposredno:
import numpy as np seznam_numpy = np.array([1, 2, 3])
kar v obeh primerih ustvari seznam oblike [1 2 3].
Podobno lahko iz podatkovnih tipov list ustvarimo tudi dvo in več dimenzionalne sezname. Na primer:
import numpy as np
seznam_2D_list = [[1, 2, 3],[4, 5, 6]]
seznam_numpy_2D = np.array(seznam_2D_list)
seznam_3D_list = [[[1, 2, 3],[4, 5, 6]],
[[7, 8, 9],[10, 11, 12]]]
seznam_numpy_3D = np.array(seznam_3D_list)
kjer najprej ustvarimo 2D seznam, ki je oblike:
[[1 2 3] [4 5 6]]
nato še 3D seznam oblike:
[[[ 1 2 3] [ 4 5 6]] [[ 7 8 9] [10 11 12]]]
2.1.2. np.zeros(), np.ones(), np.full()
Poleg funkcije np.array() lahko ustvarimo sezname še na druge načine.
Na primer:
-
funkcija
np.zeros()ustvari seznam, kjer so vsi elementi enaki 0, -
funkcija
np.ones()ustvari seznam, kjer so vsi elementi enaki 1, -
funkcija
np.full()ustvari seznam, kjer imajo vsi elementi poljubno vrednost.
Pri vseh zgornjih funkcijah kot parameter nastopa tudi dimenzija seznama. Na primer:
import numpy as np seznam_0 = np.zeros(3) seznam_1 = np.ones(4) seznam_2 = np.full(5, 2.) seznam_zeros_2D = np.zeros((2,3)) seznam_ones_3D = np.zeros((2,3,4)) seznam_full_2D = np.full((2,3),3)
kjer smo najprej ustvarili seznam s tremi ničlami [0 0 0], nato seznam s štirimi enkami [1. 1. 1. 1.], sledi seznam s petimi dvojkami [2. 2. 2. 2. 2.], nato smo ustvarili 2D seznam z ničlami:
[[0. 0. 0.] [0. 0. 0.]]
nato 3D seznam z enkami:
[[[1. 1. 1. 1.] [1. 1. 1. 1.] [1. 1. 1. 1.]] [[1. 1. 1. 1.] [1. 1. 1. 1.] [1. 1. 1. 1.]]]
in na koncu še 2D seznam s trojkami:
[[3 3 3] [3 3 3]]
2.1.3. np.random.random(), np.random.randn()
V kolikor bi radi ustvarili seznam naključnih števil, lahko uporabimo:
-
funkcijo
np.random.random(), ki generira naključna števila med 0 in 1, ali pa -
funkcijo
np.random.randn(), ki ustvarja naključne vrednosti, ki ustrezajo normalni porazdelitvi z aritmetično sredino 0 in standardnim odklonom 1.
import numpy as np seznam_0 = np.random.random(4) seznam_1 = np.random.randn(5) seznam_random_3D = np.random.random((2,3,4)) seznam_randn_2D = np.random.randn(2,3,4)
V zgornji programski kodi smo najprej ustvarili seznam s štirimi naključnimi števili med 0 in 1 [0.48919153 0.37661206 0.82123356 0.12992426], nato seznam s petimi elementi [-0.79611779 0.69580781 -0.17002363 1.0144476 1.11151188], sledi mu naključni 3D seznam:
[[[0.34266366 0.85709128 0.53028222 0.39594552] [0.46052613 0.12232418 0.51135007 0.39929888] [0.24536472 0.15279226 0.17880979 0.35304374]] [[0.9157075 0.73993641 0.00146697 0.252301 ] [0.07161547 0.59074746 0.91014181 0.26519995] [0.64553695 0.53732667 0.98011274 0.67180845]]]
in na koncu še 2D naključni seznam z normalno porazdelitvijo:
[[-0.27083714 -0.40626521 0.59413101] [-0.51287891 0.30977327 1.11657568]]
|
Vrednosti v zgornjih seznamih so naključne in se spremijo vsakič, ko izvrednotimo programsko kodo. |
2.1.4. np.linspace()
V kolikor bi radi interval razdelili na določeno število vmesnih točk, uporabimo funkcijo np.linspace(), kot na primer:
import numpy as np seznam = np.linspace(1,7,5)
kjer ustvarimo seznam s petimi točkami na intervalu med 1 in 7, ki je oblike [1. 2.5 4. 5.5 7.].
2.1.5. np.arange()
Funkcija np.arange() deluje podobno kot Python-ova funkcija range(), le da ni omejena na cela števila.
import numpy as np seznam = np.arange(1,7,1.2)
V zgornji kodi smo interval med 1 in 7 razdelili na podintervale dolžine 1.2, kar ustvari seznam [1. 2.2 3.4 4.6 5.8].
|
Funkcija |
2.1.6. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Ustvarjanje seznamov. Rešitve nalog najdete v razdelku Rešitve.
-
Pripravi in izpiši seznam
seznam_0, ki vsebuje števila od 1 do 5. -
Pripravi in izpiši seznam
seznam_1, ki vsebuje števila od 6 do 9. Uporabi funkcijorange(). -
Pripravi in izpiši seznam
seznam_2, ki vsebuje 5 elementov z vrednostjo 0. -
Pripravi in izpiši seznam
seznam_3, ki vsebuje 5 elementov z vrednostjo 1. -
Pripravi in izpiši seznam
seznam_4, ki vsebuje 5 elementov z naključno vrednostjo med 0 in 1. -
Pripravi in izpiši seznam
seznam_5, ki vsebuje 5 elementov z normalno naključno porazdelitvijo. -
Pripravi in izpiši seznam
seznam_6, ki vsebuje 3 vrednosti med 0 in 10 ter z enakomernim razmikom med njimi. -
Pripravi in izpiši seznam
seznam_7, ki vsebuje števila med 0 in 10 z razmakom 2. Uporabi funkcijonp.arange(). -
Pripravi in izpiši seznam
seznam_8, ki vsebuje 5 elementov z vrednostjo 1. Uporabi funkcijonp.full(). -
Pripravi in izpiši seznam
seznam_2D_list, ki v prvi vrstici vsebuje števila od 1 do 3 ter v drugi vrstici števila 4 do 6. -
Pripravi in izpiši seznam
seznam_3D_list, kjer je prvi sloj enak seznamuseznam_2D_list, drugi sloj pa vsebuje v prvi vrstici števila od 7 do 9 ter v drugi vrstici števila 10 do 12. -
Pripravi in izpiši seznam
seznam_zeros_2D, ki vsebuje 2 vrstici in 3 stolpce samih ničel. Uporabi funkcijonp.zeros(). -
Pripravi in izpiši seznam
seznam_ones_3D, ki vsebuje 2 sloja, 3 vrstice in 4 stolpce samih enic. Uporabi funkcijonp.ones(). -
Pripravi in izpiši seznam
seznam_full_2D, ki vsebuje 2 vrstici in 3 stolpce samih trojk. Uporabi funkcijonp.full(). -
Pripravi in izpiši seznam
seznam_random_3D, ki vsebuje 2 sloja, 3 vrstice in 4 stolpce naključnih vrednosti. -
Pripravi in izpiši seznam
seznam_randn_2D, ki vsebuje 2 vrstici in 3 stolpce naključnih vrednosti z normalno porazdelitvijo. -
Pripravi in izpiši seznam
seznam_empty_3D, ki vsebuje 2 sloja, 3 vrstice in 4 stolpce in nima predpisanih vrednosti. Uporabi funkcijonp.empty().
2.1.7. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import numpy as np
############
# 1D seznami
############
# seznam iz lista
seznam_0 = np.array([1,2,3,4,5])
print("iz lista", seznam_0)
# seznam iz range-a
seznam_1 = np.array(range(6,10))
print("iz range-a", seznam_1)
# seznam ničel
seznam_2 = np.zeros(5)
print("seznam ničel", seznam_2)
# seznam enic
seznam_3 = np.ones(5)
print("seznam enic", seznam_3)
# naključna števila
seznam_4 = np.random.random(5)
print("random", seznam_4)
# naključen seznam z normalno porazdelitvijo
seznam_5 = np.random.randn(5)
print("normalna porazdelitev", seznam_5)
# seznam z enakomernim razmakom med številkami
seznam_6 = np.linspace(0, 10, 3)
print("enakomeren razmak", seznam_6)
# seznam z arange
seznam_7 = np.arange(0, 11, 2)
print("arange", seznam_7)
# predpisana vrednost
seznam_8 = np.full(5,1.)
print("predpisana vrednost", seznam_8)
###############
# 2D/3D seznami
###############
# 2D iz list-a
seznam_2D_list = [[1, 2, 3],[4, 5, 6]]
seznam_numpy_2D = np.array(seznam_2D_list)
print("seznam_2D_list\n", seznam_numpy_2D)
# 3D iz list-a
seznam_3D_list = [[[1, 2, 3],[4, 5, 6]],
[[7, 8, 9],[10, 11, 12]]]
seznam_numpy_3D = np.array(seznam_3D_list)
print("seznam_2D_list\n", seznam_numpy_3D)
# 2D seznam ničel
seznam_zeros_2D = np.zeros((2,3))
print("seznam_zeros_2D\n", seznam_zeros_2D)
# 3D seznam enic
seznam_ones_3D = np.ones((2,3,4))
print("seznam_ones_3D\n", seznam_ones_3D)
# 2D seznam z vrednostmi 3
seznam_full_2D = np.full((2,3),3)
print("seznam_full_2D\n", seznam_full_2D)
# 3D naključen seznam
seznam_random_3D = np.random.random((2,3,4))
print("seznam_random_3D\n", seznam_random_3D)
# 2D seznam z normalno porazdelitvijo
seznam_randn_2D = np.random.randn(2,3)
print("seznam_randn_2D\n", seznam_randn_2D)
# 3D prazen seznam
seznam_empty_3D = np.empty((2,3,4))
print("seznam_empty_3D\n", seznam_empty_3D)
iz lista [1 2 3 4 5] iz range-a [6 7 8 9] seznam ničel [0. 0. 0. 0. 0.] seznam enic [1. 1. 1. 1. 1.] random [0.22698497 0.58858667 0.75416968 0.01295893 0.12006102] normalna porazdelitev [ 0.72476733 0.47211282 -1.52345608 0.78531476 -1.75543055] enakomeren razmak [ 0. 5. 10.] arange [ 0 2 4 6 8 10] predpisana vrednost [1. 1. 1. 1. 1.] seznam_2D_list [[1 2 3] [4 5 6]] seznam_2D_list [[[ 1 2 3] [ 4 5 6]] [[ 7 8 9] [10 11 12]]] seznam_zeros_2D [[0. 0. 0.] [0. 0. 0.]] seznam_ones_3D [[[1. 1. 1. 1.] [1. 1. 1. 1.] [1. 1. 1. 1.]] [[1. 1. 1. 1.] [1. 1. 1. 1.] [1. 1. 1. 1.]]] seznam_full_2D [[3 3 3] [3 3 3]] seznam_random_3D [[[0.81687724 0.1316954 0.43249378 0.68183805] [0.24865459 0.46379858 0.45217242 0.68531292] [0.71744644 0.96624331 0.59466896 0.7927558 ]] [[0.58785492 0.62404746 0.37233981 0.44714767] [0.62235022 0.9475961 0.19247777 0.63526505] [0.28919388 0.96775128 0.58987585 0.15418241]]] seznam_randn_2D [[ 0.57894841 -1.57132949 1.47556929] [-0.43090203 0.57412793 -0.90833248]] seznam_empty_3D [[[0.81687724 0.1316954 0.43249378 0.68183805] [0.24865459 0.46379858 0.45217242 0.68531292] [0.71744644 0.96624331 0.59466896 0.7927558 ]] [[0.58785492 0.62404746 0.37233981 0.44714767] [0.62235022 0.9475961 0.19247777 0.63526505] [0.28919388 0.96775128 0.58987585 0.15418241]]]
2.2. Indeksiranje numpy seznamov
Podobno kot pri podatkovni strukturi list dostopamo do posameznih elementov seznama numpy z zaporedno številko elementa (angl. array index).
Kot pri vseh ostalih indeksiranih podatkovnih strukturah Python, se tudi pri seznamu numpy številčenje oziroma indeksiranje elementov začne s števiko 0.
2.2.1. Vrednosti elementov
Pri 1D seznamih numpy je indeksiranje povsem identično kot pri podatkovnem tipu list:
seznam[indeks]
kjer indeks določa indeks oziroma zaporedno številko elementa v seznamu, ki bi ga radi dobili.
Na primer do posameznih elementov seznama seznam = np.array([1, 2, 3, 4, 5, 6, 7])
dostopamo na naslednje načine:
-
seznam[0]- nam vrne prvi element (vrednost 1), -
seznam[3]- nam vrne četrti element (vrednost 4), -
seznam[6]- nam vrne sedmi element (vrednost 7), -
seznam[-1]- nam vrne zadnji element (vrednost 7), -
seznam[-3]- nam vrne tretji element iz zadnje strani (vrednost 5), -
itd.
Indeksiranje večdimenzionalnih seznamov je podobno kot pri 1D seznamih, le da je potrebno za vsako dodatno dimenzijo navesti dodaten indeks. Pri 2D seznamih je posamezen element določen z indeksom vrstice in indeksom stolpca:
seznam_2D[indeks_vrstice, indeks_stolpca]
pri 3D seznamih pa je potrebno dodati še indeks sloja:
seznam_3D[indeks_sloja, indeks_vrstice, indeks_stolpca]
2.2.2. Urejanje elementov
Tudi urejanje posameznih elementov 1D seznama numpy poteka identično kot pri tipu list, in sicer:
seznam[indeks] = nova_vrednost
kjer indeks določa zaporedno številko elementa v seznamu, ki ga popravljamo, nova_vrednost pa je nova vrednost, s katero bomo povozili trenutno vrednost elementa seznam[indeks].
Na primer, če bi radi popravili nekaj elementov iz seznama seznam = np.array([1, 2, 3, 4, 5, 6, 7]), lahko to storimo z naslednjo programsko kodo:
# popravimo 1. element seznam[0] = 2 # popravimo 4. element seznam[3] = 3 # popravimo 7. element seznam[6] = 4 # popravimo zadnji element seznam[-1] = 5 # tretji element iz zadnje strani seznam[-3] = 6
Končna vrednost seznama po izvrednotenju zgornje programske kode je [2 2 3 3 6 6 5].
Pri urejanju posameznih elementov 2D seznamov moramo navesti indeks vrstice in indeks stolpca:
seznam_2D[indeks_vrstice, indeks_stolpca] = nova_vrednost
oziroma pri 3D seznamih je potrebno navesti še indeks sloja:
seznam_3D[index_sloja, indeks_vrstice, indeks_stolpca] = nova_vrednost
2.2.3. Napredno indeksiranje
Indeksiranje seznamov numpy ni omejeno le na posamezen element, ampak lahko dostopamo oz. spreminjamo tudi več elementov naenkrat.
Vrednosti elementov
Sintaksa je v primeru naprednega indeksiranja naslednja:
seznam[seznam_indeksov]
kjer seznam_indeksov določa seznam, v katerem so zapisani indeksi elementov, ki bi jih radi dobili.
Na primer, če bi radi iz seznama seznam = np.array([1, 2, 3, 4, 5, 6, 7, 8]) dobili elemente na indeksih 5, 2, in -1, lahko to storimo z naslednjo programsko kodo:
izbrani_elementi = seznam[[5, 2, -1]] print(izbrani_elementi) # izpis: [6 3 8]
kjer smo v spremenljivko izbrani_elementi shranili seznam z željenimi vrednostmi.
Indeksiranje seznamov numpy nam omogoča tudi, da iz obstoječega seznama določimo nov seznam, ki je lahko poljubnih dimnezij. In sicer je dimenzija novega seznama določena s seznamom indeksov. Na primer programska koda:
izbrani_elementi = seznam[[[1, 2, 3],[4, 5, 6]]] print(izbrani_elementi) # izpis: [[2 3 4] [5 6 7]]
ustvari dvodimenzionalni seznam izbrani_elementi, ki vsebuje izbrane vrednosti iz 1D seznama seznam.
Napredno indeksiranje seveda ni omejeno le na 1D sezname. Na primer:
seznam_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) izbrani_stolpci = seznam_2d[:,[1,2]] print(izbrani_stolpci) # izpis: [[2 3] [6 7] [10 11]]
iz seznama seznam_2d pridobi elemente, ki so v stolpcih z ideksom 1 in 2.
Urejanje elementov
Z naprednim indeksiranjem lahko tudi popravimo vrednosti večih elementov hkrati. Sintaksa je v temu primeru naslednja:
seznam[seznam_indeksov] = nove_vrednosti
oziroma v konkternem primer nam programska koda:
seznam[[4, 5, 6]] = [9 , 10 , 11] print(seznam) # izpis: [1 2 3 4 9 10 11 8]
popravi vrednosti na indeksih 4, 5 in 6.
2.2.4. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Indeksiranje numpy seznamov. Rešitve nalog najdete v razdelku Rešitve.
-
Pripravi seznam
seznam_1D, ki vsebuje števila od 1 do 7. -
Izpiši 1. element seznama.
-
Izpiši 4. element seznama.
-
Izpiši 7. element seznama.
-
Izpiši zadnji element seznama.
-
Izpiši 3. element z zadnje strani seznama.
-
Popravi 1. element seznama in mu priredi vrednost 2.
-
Popravi 4. element seznama in mu priredi vrednost 3.
-
Popravi 7. element seznama in mu priredi vrednost 4.
-
Popravi zadnji element seznama in mu priredi vrednost 5.
-
Popravi 3. element z zadnje strani seznama in mu priredi vrednost 6.
-
Pripravi seznam
seznam_2D, ki je oblike [[1, 2, 3],[4, 5, 6],[7, 8, 9]]. -
Izpiši element na poziciji 0, 0.
-
Izpiši element na poziciji -3, -3.
-
Izpiši element na poziciji 2, 2.
-
Izpiši element na poziciji -1, -1.
-
Izpiši element na poziciji 1, 1.
-
Izpiši element na poziciji -2, -2.
-
Popravi element na poziciji -3, -3 in mu priredi vrednost 12.
-
Popravi element na poziciji 2, 2 in mu priredi vrednost 13.
-
Popravi element na poziciji -1, -1 in mu priredi vrednost 14.
-
Popravi element na poziciji 1, 1 in mu priredi vrednost 15.
-
Popravi element na poziciji -2, -2 in mu priredi vrednost 16.
-
Pripravi seznam
seznam_3D, ki je oblike [[[1, 2, 3],[4, 5, 6],[7, 8, 9]],[[11, 12, 13],[14, 15, 16],[17, 18, 19]]]. -
Izpiši element na poziciji 0, 0, 0.
-
Izpiši element na poziciji -2, -3, -3.
-
Izpiši element na poziciji 1, 2, 2.
-
Izpiši element na poziciji -1, -1, -1.
-
Izpiši element na poziciji 1, 1, 1.
-
Izpiši element na poziciji -2, -2, -2.
-
Popravi element na poziciji -3, -3, 1 in mu priredi vrednost 112.
-
Popravi element na poziciji 1, 2, 2 in mu priredi vrednost 113.
-
Popravi element na poziciji -1, -1, -1 in mu priredi vrednost 114.
-
Popravi element na poziciji 1, 1, 1 in mu priredi vrednost 115.
-
Popravi element na poziciji -2, 2, -2 in mu priredi vrednost 116.
2.2.5. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
import numpy as np
#########################
#########################
# 1D SEZNAMI #
#########################
#########################
print("1D")
# pripravimo seznam
seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7])
#########################
# dostopanje do elementa#
#########################
# izpišemo prvi element
print("1. element", seznam_1D[0])
# izpišemo 4. element
print("4. element", seznam_1D[3])
# izpišemo 7. element
print("7. element", seznam_1D[6])
# izpišemo zadnji element
print("-1. element", seznam_1D[-1])
# izpišemo tretji element iz zadnje strani
print("-3. element", seznam_1D[-3])
#########################
# urejanje elementa #
#########################
# popravimo 1. element
seznam_1D[0] = 2
# popravimo 4. element
seznam_1D[3] = 3
# popravimo 7. element
seznam_1D[6] = 4
# popravimo zadnji element
seznam_1D[-1] = 5
# tretji element iz zadnje strani
seznam_1D[-3] = 6
print("popravljen seznam_1D\n", seznam_1D)
#########################
#########################
# 2D SEZNAMI #
#########################
#########################
print("\n2D")
# pripravimo seznam
seznam_2D = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
#########################
# dostopanje do elementa#
#########################
# izpišemo element 0, 0
print("element 0, 0:", seznam_2D[0, 0])
# izpišemo element -3, -3
print("element -3, -3:",seznam_2D[-3, -3])
# izpišemo element 2, 2
print("element 2, 2:",seznam_2D[2, 2])
# izpišemo element -1, -1
print("element -1, -1:",seznam_2D[-1, -1])
# izpišemo element 1, 1
print("element 1, 1:",seznam_2D[1, 1])
# izpišemo element -2, -2
print("element -2, -2:",seznam_2D[-2, -2])
#########################
# urejanje elementa #
#########################
# popravimo element -3, -3
seznam_2D[-3, -3] = 12
# popravimo element 2, 2
seznam_2D[2, 2] = 13
# popravimo element -1, -1
seznam_2D[-1, -1] = 14
# popravimo element 1, 1
seznam_2D[1, 1] = 15
# popravimo element -2, -2
seznam_2D[-2, -2] = 16
print("popravljen seznam_2D\n", seznam_2D)
#########################
#########################
# 3D SEZNAMI #
#########################
#########################
print("\n3D")
# pripravimo seznam
seznam_3D = np.array([[[1, 2, 3],[4, 5, 6],[7, 8, 9]],[[11, 12, 13],[14, 15, 16],[17, 18, 19]]])
#########################
# dostopanje do elementa#
#########################
# izpišemo element 0, 0, 0
print("element 0, 0, 0:", seznam_3D[0, 0, 0])
# izpišemo element -2, -3, -3
print("element -2, -3, -3:",seznam_3D[-2, -3, -3])
# izpišemo element 1, 2, 2
print("element 1, 2, 2:",seznam_3D[1, 2, 2])
# izpišemo element -1, -1, -1
print("element -1, -1, -1:",seznam_3D[-1, -1, -1])
# izpišemo element 1, 1, 1
print("element 1, 1, 1:",seznam_3D[1, 1, 1])
# izpišemo element -2, -2, -2
print("element -2, -2, -2:",seznam_3D[-2, -2, -2])
#########################
# urejanje elementa #
#########################
# popravimo element -3, -3, 1
seznam_3D[0, -3, 1] = 112
# popravimo element 1, 2, 2
seznam_3D[1, 2, 2] = 113
# popravimo element -1, -1, -1
seznam_3D[-1, -1, -1] = 114
# popravimo element 1, 1, 1
seznam_3D[1, 1, 1] = 115
# popravimo element -2, 2, -2
seznam_3D[-2, 2, -2] = 116
print("popravljen seznam_3D\n", seznam_3D)
1D 1. element 1 4. element 4 7. element 7 -1. element 7 -3. element 5 popravljen seznam_1D [2 2 3 3 6 6 5] 2D element 0, 0: 1 element -3, -3: 1 element 2, 2: 9 element -1, -1: 9 element 1, 1: 5 element -2, -2: 5 popravljen seznam_2D [[12 2 3] [ 4 16 6] [ 7 8 14]] 3D element 0, 0, 0: 1 element -2, -3, -3: 1 element 1, 2, 2: 19 element -1, -1, -1: 19 element 1, 1, 1: 15 element -2, -2, -2: 5 popravljen seznam_3D [[[ 1 112 3] [ 4 5 6] [ 7 116 9]] [[ 11 12 13] [ 14 115 16] [ 17 18 114]]]
2.3. Rezanje seznamov
Z rezanjem seznamov (angl. slicing) lahko na prepost način iz celotnega seznama izločimo podseznam, ali pa rezanje uporabimo za urejanje seznamov.
2.3.1. Podseznam
Sintaksa pri 1D seznamih je ekvivalentna klasični sintaksi Python:
seznam[zacetek:konec:korak]
kjer,
-
zacetekpredstavlja indeks elementa, ki bo prvi vključen v izbor, -
konec- predstavlja indeks zadnjega elementa v izboru, kateri pa ne bo vključen v izbor, -
korak- določa dolžino koraka med dvema elementoma v izboru.
Do podseznamov spodnjega seznama numpy:
seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
lahko lahko dostopamo na primer z:
-
seznam_1D[1:8:2]razrežeseznam_1Dod indeksa 1 do indeksa 8 s korakom 2, kar vrne seznam[2 4 6 8], -
seznam_1D[3:-1:3]razrežeseznam_1Dod indeksa 3 do indeksa -1 s korakom 3, kar vrne seznam[4 7], -
seznam_1D[3:6]razrežeseznam_1Dod indeksa 3 do indeksa 6 s prednastavljenim korakom, kar vrne seznam[4 5 6], -
seznam_1D[3::4]razrežeseznam_1Dod indeksa 3 do konca seznama s korakom 4, kar vrne seznam[4 8], -
seznam_1D[:8:3]razrežeseznam_1Dod začetka do indeksa 8 s korakom 3, kar vrne seznam[1 4 7], -
seznam_1D[::4]razrežeseznam_1Dod začetka do konca s korakom 4, kar vrne seznam[1 5 9], -
seznam_1D[:4:]razrežeseznam_1Dod začetka do indeksa 4 s prednastavljenim korakom, kar vrne seznam[1 2 3 4], -
seznam_1D[4::]razrežeseznam_1Dod indeksa 4 do konca s prednastavljenim korakom, kar vrne seznam[5 6 7 8 9]. -
seznam_1D[-3:]razrežeseznam_1Dod indeksa -3 do konca s prednastavljenim korakom, kar vrne seznam[7 8 9], -
seznam_1D[-5:-2]razrežeseznam_1Dod indeksa -5 do indeksa -2 s prednastavljenim korakom, kar vrne seznam[5 6 7], -
seznam_1D[-1::-2]razrežeseznam_1Dod indeksa -1 do začetka seznama s korakom -2, kar vrne seznam[9 7 5 3 1], -
seznam_1D[::-1]razrežeseznam_1Ds korakom -1, kar dejansko vrne obrnjen seznam[9 8 7 6 5 4 3 2 1].
Sintaksa pri večdimenzionalnih seznamih je podobna, le da je za vsako dodatno dimenzijo potrebno navesti vse tri parametre (začetni indeks, končni indeks in korak). V primeru 2D seznamov je sintaksa sledeča:
seznam_2D[zac_vrstica:kon_vrstica:korak_vrstica, zac_stolpec:kon_stolpec:korak_stolpec]
2.3.2. Urejanje podseznamov
Rezanje lahko uporabimo tudi za urejanje seznamov. Sintaksa je povsem identična kot v prejšnjem razdelku, le da je za ureditev podseznama potrebno podati tudi novo vrednost:
seznam[zacetek:konec:korak] = nova_vrednost
oziroma v primeru 2D seznamov:
seznam_2D[zac_vrstica:kon_vrstica:korak_vrstica, zac_stolpec:kon_stolpec:korak_stolpec] = nova_vrednost
kjer nova_vrednost predstavlja novo vrednost, ki se bo zapisala v izbrane elemente. Nova vrednost je lahko skalar, če vsem elementom priredimo enako vrednost.
Lahko pa za novo_vrednost podamo tudi eno ali več dimenzionalni seznam, če elementom prirejamo različne vrednosti.
Nekaj primerov urejanja 1D seznamov je navedenih spodaj, kjer smo za izvorni seznam vedno vzeli seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]):
-
seznam_1D[1:8:2] = 0, kjer vsem elementom podseznama, določenega z začetnim indeksom 1, končnim indeksom 8 in korakom 2 priredimo vrednost 0. Po opreaciji je vsebinaseznam_1Denaka[1 0 3 0 5 0 7 0 9]. -
seznam_1D[3:-1:3] = [10, 20], kjer uredimo podseznam, določen z začetnim indeksom 3, končnim indeksom -1 in korakom 3 in mu priredimo novo vrednost [10, 20]. Po opreaciji je vsebinaseznam_1Denaka[ 1 2 3 10 5 6 20 8 9]. -
seznam_1D[-5:-2] = [1, 2, 3], kjer uredimo podseznam, določen z začetnim indeksom -5 in končnim indeksom -2 in mu priredimo novo vrednost [1, 2, 3]. Po opreaciji je vsebinaseznam_1Denaka[1 2 3 4 1 2 3 8 9]. -
seznam_1D[-1::-2] = 15, kjer vsem elementom podseznama, določenega z začetnim indeksom -1 in korakom -2 priredimo vrednost 15. Po opreaciji je vsebinaseznam_1Denaka[15 2 15 4 15 6 15 8 15].
2.3.3. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Rezanje seznamov. Rešitve nalog najdete v razdelku Rešitve.
-
Definiraj seznam
seznam_1D, ki vsebuje števila od 1 do 9. -
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od 1 do 8 s korakom 2.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od 3 do -1 s korakom 3.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od 3 do 6.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od 3 do konca s korakom 4.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente od začetka seznama do indeksa 8 s korakom 3.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente od začetka do konca seznama s korakom 4.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente od začetka seznama do indeksa 4.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od 4 do konca seznama.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od -3 do konca seznama.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od -5 do -2.
-
Z rezanjem izpiši podseznam, ki vsebuje elemente na indeksih od -1 do začetka seznama s korakom -2.
-
Z rezanjem izpiši seznam v obratnem vrstnem redu.
-
Definiraj seznam
seznam_1D, ki vsebuje števila od 1 do 9. Podseznamu, ki je na indeksih od 1 do 8 s korakom 2, priredi vrednosti 0 za vse elemente. Izpiši seznamseznam_1D. -
Definiraj seznam
seznam_1D, ki vsebuje števila od 1 do 9. Podseznamu, ki je na indeksih od 3 do -1 s korakom 3, priredi vrednost[10, 20]. Izpiši seznamseznam_1D. -
Definiraj seznam
seznam_1D, ki vsebuje števila od 1 do 9. Podseznamu, ki je na indeksih od -5 do -2, priredi vrednost [1, 2, 3]. Izpiši seznamseznam_1D. -
Definiraj seznam
seznam_1D, ki vsebuje števila od 1 do 9. Podseznamu, ki je na indeksih od -1 do začetka, priredi vrednosti 15 za vse elemente. Izpiši seznamseznam_1D. -
Definiraj seznam
seznam_2D, ki v treh vrsticah in štirih stolpcih vsebuje števila od 1 do 12. -
Z rezanjem izpiši podseznam, ki vsebuje presek prvih dveh vrstic in prvih dveh stolpcev.
-
Z rezanjem izpiši podseznam, ki vsebuje presek zadnjih dveh vrstic in zadnjih dveh stolpcev.
-
Z rezanjem izpiši podseznam, ki vsebuje presek 1. in 3. vrstice ter 2. in 4. stolpca.
-
Z rezanjem izpiši podseznam, ki vsebuje prvo vrstico.
-
Z rezanjem izpiši podseznam, ki vsebuje drugi stolpec.
-
Definiraj seznam
seznam_2D, ki v treh vrsticah in štirih stolpcih vsebuje števila od 1 do 12. Podseznamu, ki je presek prvih dveh vrstic in prvih dveh stolpcev, priredi vrednosti 0 za vse elemente. Izpiši seznamseznam_2D. -
Definiraj seznam
seznam_2D, ki v treh vrsticah in štirih stolpcih vsebuje števila od 1 do 12. Podseznamu, ki je presek zadnjih dveh vrstic in zadnjih dveh stolpcev, priredi vrednost [[ 15, 16], [17, 18]]. Izpiši seznamseznam_2D. -
Definiraj seznam
seznam_2D, ki v treh vrsticah in štirih stolpcih vsebuje števila od 1 do 12. Podseznamu, ki je presek presek 1. in 3. vrstice ter 2. in 4. stolpca, priredi vrednost [[2, 4], [10, 12]]. Izpiši seznamseznam_2D. -
Definiraj seznam
seznam_2D, ki v treh vrsticah in štirih stolpcih vsebuje števila od 1 do 12. Podseznamu, ki vsebuje prvo vrstico, priredi vrednosti 15 za vse elemente. Izpiši seznamseznam_2D. -
Definiraj seznam
seznam_2D, ki v treh vrsticah in štirih stolpcih vsebuje števila od 1 do 12. Podseznamu, ki vsebuje drugi stolpec, priredi vrednosti [15, 16, 17]. Izpiši seznamseznam_2D.
2.3.4. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
import numpy as np
#########################
#########################
# REZANJE 1D SEZNAMOV #
#########################
#########################
print("1D")
# pripravimo seznam
seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
print("seznam_1D", seznam_1D)
# rez od indeksa 1 do 8 s korakom 2
print("seznam_1D[1:8:2]", seznam_1D[1:8:2])
# rez od indeksa 3 do -1 s korakom 3
print("seznam_1D[3:-1:3]", seznam_1D[3:-1:3])
# rez od indeksa 3 do 6
print("seznam_1D[3:6]", seznam_1D[3:6])
# rez od indeksa 3 do konca s korakom 4
print("seznam_1D[3::4]", seznam_1D[3::4])
# rez od začetka do indeksa 8 s korakom 3
print("seznam_1D[:8:3]", seznam_1D[:8:3])
# rez od začetka do konca s korakom 4
print("seznam_1D[::4]", seznam_1D[::4])
# rez od začetka do indeksa 4
print("seznam_1D[:4:]", seznam_1D[:4:])
# rez od indeksa 4 do konca
print("seznam_1D[4::]", seznam_1D[4::])
# rez od indeksa -3 do konca
print("seznam_1D[-3:]", seznam_1D[-3:])
# rez od indeksa -5 do indeksa -2
print("seznam_1D[-5:-2]", seznam_1D[-5:-2])
# rez od indeksa -1 do začetka s korakom -2
print("seznam_1D[-1::-2]", seznam_1D[-1::-2])
# obrnjen seznam
print("seznam_1D[::-1]", seznam_1D[::-1])
#########################
#########################
# UREJANJE 1D SEZNAMOV #
#########################
#########################
print("1D urejanje")
seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
seznam_1D[1:8:2] = 0
print("seznam_1D[1:8:2] = 0 - >", seznam_1D)
seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
seznam_1D[3:-1:3] = [10, 20]
print("seznam_1D[3:-1:3] = [10, 20] - >", seznam_1D)
seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
seznam_1D[-5:-2] = [1, 2, 3]
print("seznam_1D[-5:-2] = [1, 2, 3] - >", seznam_1D)
seznam_1D = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
seznam_1D[-1::-2] = 15
print("seznam_1D[-1::-2] = 15 - >", seznam_1D)
#########################
#########################
# REZANJE 2D SEZNAMOV #
#########################
#########################
print("2D")
# pripravimo seznam
seznam_2D = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
print("seznam_2D\n", seznam_2D)
# prvi dve vrstici in stolpca
print("seznam_2D[:2, :2]\n", seznam_2D[:2, :2])
# zadnji dve vrstici in stolpca
print("seznam_2D[-2:, -2:]\n", seznam_2D[-2:, -2:])
# zadnji 1. in 3. vrstica in 2. in 4. stolpec
print("seznam_2D[0::2, 1::2]\n", seznam_2D[0::2, 1::2])
# celotna prva vrstica
print("seznam_2D[0, :]\n", seznam_2D[0, :])
# celoten drugi stolpce
print("seznam_2D[:, 1]\n", seznam_2D[:, 1])
#########################
#########################
# UREJANJE 2D SEZNAMOV #
#########################
#########################
print("2D urejanje")
seznam_2D = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
seznam_2D[:2, :2] = 0
print("seznam_2D[:2, :2] = 0\n", seznam_2D)
seznam_2D = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
seznam_2D[-2:, -2:] = [[ 15, 16], [17, 18]]
print("seznam_2D[-2:, -2:] = [[ 15, 16], [17, 18]]\n", seznam_2D)
seznam_2D = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
seznam_2D[0::2, 1::2] = np.array([[2, 4], [10, 12]])
print("seznam_2D[0::2, 1::2] = np.array([[2, 4], [10, 12]])\n", seznam_2D)
seznam_2D = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
seznam_2D[0, :] = 15
print("seznam_2D[0, :] = 15\n", seznam_2D)
seznam_2D = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
seznam_2D[:, 1] = np.array([15, 16, 17])
print("seznam_2D[:, 1] = np.array([15, 16, 17])\n", seznam_2D)
1D seznam_1D [1 2 3 4 5 6 7 8 9] seznam_1D[1:8:2] [2 4 6 8] seznam_1D[3:-1:3] [4 7] seznam_1D[3:6] [4 5 6] seznam_1D[3::4] [4 8] seznam_1D[:8:3] [1 4 7] seznam_1D[::4] [1 5 9] seznam_1D[:4:] [1 2 3 4] seznam_1D[4::] [5 6 7 8 9] seznam_1D[-3:] [7 8 9] seznam_1D[-5:-2] [5 6 7] seznam_1D[-1::-2] [9 7 5 3 1] seznam_1D[::-1] [9 8 7 6 5 4 3 2 1] 1D urejanje seznam_1D[1:8:2] = 0 - > [1 0 3 0 5 0 7 0 9] seznam_1D[3:-1:3] = [10, 20] - > [ 1 2 3 10 5 6 20 8 9] seznam_1D[-5:-2] = [1, 2, 3] - > [1 2 3 4 1 2 3 8 9] seznam_1D[-1::-2] = 15 - > [15 2 15 4 15 6 15 8 15] 2D seznam_2D [[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] seznam_2D[:2, :2] [[1 2] [5 6]] seznam_2D[-2:, -2:] [[ 7 8] [11 12]] seznam_2D[0::2, 1::2] [[ 2 4] [10 12]] seznam_2D[0, :] [1 2 3 4] seznam_2D[:, 1] [ 2 6 10] 2D urejanje seznam_2D[:2, :2] = 0 [[ 0 0 3 4] [ 0 0 7 8] [ 9 10 11 12]] seznam_2D[-2:, -2:] = [[ 15, 16], [17, 18]] [[ 1 2 3 4] [ 5 6 15 16] [ 9 10 17 18]] seznam_2D[0::2, 1::2] = np.array([[2, 4], [10, 12]]) [[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] seznam_2D[0, :] = 15 [[15 15 15 15] [ 5 6 7 8] [ 9 10 11 12]] seznam_2D[:, 1] = np.array([15, 16, 17]) [[ 1 15 3 4] [ 5 16 7 8] [ 9 17 11 12]]
2.4. Transponiranje seznamov
Funkcija np.transpose() nam omogoče transponiranje seznamov z naslednjo sintakso:
transponiran_seznam = np.transpose(originalen_seznam)
Pri 2D seznamih se pri transponiranju stolpci zamenjajo z vrsticami oziroma je obnašanje povsem identično kot pri transponiranju matrik. Na primer seznam:
seznam_2D = np.array([[1, 2],[3, 4]])
oziroma izpisana vrednost seznam_2D:
[[1 2] [3 4]]
se po transponiranju:
transponiran_seznam_2D = np.transpose(seznam_2D)
preoblikuje v:
[[1 3] [2 4]]
|
Namesto ukaza |
|
Omogočeno je tudi transponiranje tri in več dimenzionalnih seznamov, kjer je potrebno navesti še dodaten argument, s katerim določimo, katere osi se bodo zamenjale med seboj. transponiran_seznam = np.transpose(originalen_seznam, nov_vrstni_red_osi) |
2.4.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Transponiranje seznamov. Rešitve nalog najdete v razdelku Rešitve.
-
Pripravi seznam
seznam_1D, ki je oblike [1, 2, 3, 4]. -
Pripravi seznam
seznam_2D, ki je oblike [[1, 2],[3, 4]]. -
Pripravi seznam
seznam_3D, ki je oblike [[[1, 2],[3, 4]],[[5, 6],[7, 8]]]. -
Transponiraj seznam
seznam_1Din ga shrani v spremenljivkotransponiran_seznam_1D. -
Izpiši vrednosti originalnega in transponiranega seznama.
-
Transponiraj seznam
seznam_2Din ga shrani v spremenljivkotransponiran_seznam_2D. -
Izpiši vrednosti originalnega in transponiranega seznama.
-
Transponiraj seznam
seznam_3D, kjer stolpci zamenjajo sloje, sloji zamenjajo vrstice, vrstice zamenjajo stolpce in ga shrani v spremenljivkotransponiran_seznam_3D. -
Izpiši vrednosti originalnega in transponiranega seznama.
2.4.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
#########################
#########################
# transponiranje #
#########################
#########################
# pripravimo originalne sezname
seznam_1D = np.array([1, 2, 3, 4])
seznam_2D = np.array([[1, 2],[3, 4]])
seznam_3D = np.array([[[1, 2],[3, 4]],[[5, 6],[7, 8]]])
# transponiramo 1d seznam
transponiran_seznam_1D = np.transpose(seznam_1D)
print("original 1D\n", seznam_1D)
print("transponiran 1D\n", transponiran_seznam_1D)
# transponiramo 2d seznam
transponiran_seznam_2D = np.transpose(seznam_2D)
print("original 2D\n", seznam_2D)
print("transponiran 2D\n", transponiran_seznam_2D)
# transponiramo 3d seznam z dodatnim argumentom (2, 0, 1)
# 2 - stolpci zamenjajo sloje
# 0 - sloji zamenjajo vrstice
# 1 - vrstice zamenjajo stolpce
transponiran_seznam_3D = np.transpose(seznam_3D, (2, 0, 1))
print("original 3D\n", seznam_3D)
print("transponiran 3D\n", transponiran_seznam_3D)
original 1D [1 2 3 4] transponiran 1D [1 2 3 4] original 2D [[1 2] [3 4]] transponiran 2D [[1 3] [2 4]] original 3D [[[1 2] [3 4]] [[5 6] [7 8]]] transponiran 3D [[[1 3] [5 7]] [[2 4] [6 8]]]
Poglavje 3. Matematične operacije
3.1. Aritmetične operacije na seznamih
Knjižnica numpy_ ponuja širok nabor različnih operacij, ki jih lahko izvajamo na seznamih. Najbolj pogosto se uporabljajo naslednje aritmetične operacije:
Elementarna operacija |
Operator |
Funkcija |
Seštevanje |
|
|
Odštevanje |
|
|
Množenje |
|
|
Deljenje |
|
|
Potenciranje |
|
|
Modulus |
|
|
Vse gornje funkcije oziroma operatorji delujejo po podobnem principu, in sicer lahko za vsako operacijo uporabimo ali povezani operator ali funkcijo. Primer uporabe si bomo pogledali na primeru seštevanja, kjer si za podatke izberemo naslednje spremenljivke:
seznam_1 = np.array([1, 2, 3, 4]) seznam_2 = np.array([5, 6, 7, 8]) skalar = 3
seznam_1 in seznam_2 lahko seštejemo med seboj, kar pomeni, da se bo izvedlo seštevanje po elementih, in sicer se med seboj seštejeta prva elementa (1 + 5 = 6), druga elementa (2 + 6 = 8), itd. To lahko storimo ali z uporabo operatorja +:
rezultat_1 = seznam_1 + seznam_2
ali s funkcijo np.add():
rezultat_2 = np.add(seznam_1, seznam_2)
kjer v obeh primerih dobimo rezultat:
[6, 8, 10, 12]
|
Seštevamo lahko le sezname, ki so enakih dimenzij. V kolikor se dimenzije seznamov ne ujemajo, nam Python vrne napako. |
Poleg seštevanja dveh seznamov je možno tudi seštevanje med seznamom in skalarjem:
rezultat_3 = seznam_1 + skalar
kjer se vsakemu elementu v seznamu seznam_1 prišteje vrednost skalar in dobimo rezultat:
[4, 5, 6, 7]
3.1.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Aritmetične operacije na seznamih. Rešitve nalog najdete v razdelku Rešitve.
-
pripravi seznam
seznam_1, ki je oblike [1, 2, 3, 4], seznamseznam_2, ki je oblike [5, 6, 7, 8] in sklarskalar = 3. -
Z uporabo operatorja ter z uporabo funkcije seštej seznam
seznam_1in seznamseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije seštej seznam
seznam_1in skalarskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije od seznama
seznam_1odštejseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije od seznama
seznam_1odštejskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije zmnoži seznama
seznam_1inseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije zmnoži seznam
seznam_1in skalarskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije seznam
seznam_1deli sseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije seznam
seznam_1deli s skalarjemskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije skalar
skalardeli sseznam_1ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije elemente seznama
seznam_1potenciraj z elementi seznamaseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije elemente seznama
seznam_1potenciraj s skalarjemskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije skalar
skalarpotenciraj z elementi seznamaseznam_1ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije določi ostanek (modulus), če elemente seznama
seznam_1deliš z elementi seznamaseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije določi ostanek (modulus), če elemente seznama
seznam_1deliš s skalarjemskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije določi ostanek (modulus), če skalar
skalardeliš z elementi seznamaseznam_1ter izpiši rezultate. -
pripravi seznam
seznam_1, ki je oblike [[1, 2, 3, 4],[5, 6, 7, 8]], seznamseznam_2, ki je oblike [[1, 2, 1, 2],[3, 4, 3, 4]] in sklarskalar = 3. -
Z uporabo operatorja ter z uporabo funkcije seštej seznam
seznam_1in seznamseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije seštej seznam
seznam_1in skalarskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije od seznama
seznam_1odštejseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije od seznama
seznam_1odštejskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije zmnoži seznama
seznam_1inseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije zmnoži seznam
seznam_1in skalarskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije seznam
seznam_1deli sseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije seznam
seznam_1deli s skalarjemskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije skalar
skalardeli sseznam_1ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije elemente seznama
seznam_1potenciraj z elementi seznamaseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije elemente seznama
seznam_1potenciraj s skalarjemskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije skalar
skalarpotenciraj z elementi seznamaseznam_1ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije določi ostanek (modulus), če elemente seznama
seznam_1deliš z elementi seznamaseznam_2ter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije določi ostanek (modulus), če elemente seznama
seznam_1deliš s skalarjemskalarter izpiši rezultate. -
Z uporabo operatorja ter z uporabo funkcije določi ostanek (modulus), če skalar
skalardeliš z elementi seznamaseznam_1ter izpiši rezultate.
3.1.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
import numpy as np
############
# 1D seznami
############
print("#"*10)
print("1D seznami")
print("#"*10)
seznam_1 = np.array([1, 2, 3, 4])
seznam_2 = np.array([5, 6, 7, 8])
skalar = 3
print("seznam_1\n", seznam_1)
print("seznam_2\n", seznam_2)
print("skalar\n", skalar)
# seštevanje dveh seznamov
rez_seštevanje_1 = seznam_1 + seznam_2
rez_seštevanje_2 = np.add(seznam_1, seznam_2)
print("seštevanje dveh seznamov s + in z np.add():\n", rez_seštevanje_1,"\n", rez_seštevanje_2)
# seštevanje seznama s skalarjem
rez_seštevanje_3 = seznam_1 + skalar
rez_seštevanje_4 = np.add(seznam_1, skalar)
print("seštevanje seznama s skalarjem s + in z np.add():\n", rez_seštevanje_3,"\n", rez_seštevanje_4)
# odštevanje dveh seznamov
rez_odštevanje_1 = seznam_1 - seznam_2
rez_odštevanje_2 = np.subtract(seznam_1, seznam_2)
print("odštevanje dveh seznamov z - in z np.subtract():\n", rez_odštevanje_1,"\n", rez_odštevanje_2)
# odštevanje seznama s skalarjem
rez_odštevanje_3 = seznam_1 - skalar
rez_odštevanje_4 = np.subtract(seznam_1, skalar)
print("odštevanje seznama s skalarjem z - in z np.subtract():\n", rez_odštevanje_3,"\n", rez_odštevanje_4)
# množenje dveh seznamov
rez_množenje_1 = seznam_1 * seznam_2
rez_množenje_2 = np.multiply(seznam_1, seznam_2)
print("množenje dveh seznamov z * in z np.multiply():\n", rez_množenje_1,"\n", rez_množenje_2)
# množenje seznama s skalarjem
rez_množenje_3 = seznam_1 * skalar
rez_množenje_4 = np.multiply(seznam_1, skalar)
print("množenje seznama s skalarjem z * in z np.multiply():\n", rez_množenje_3,"\n", rez_množenje_4)
# deljenje dveh seznamov
rez_deljenje_1 = seznam_1 / seznam_2
rez_deljenje_2 = np.divide(seznam_1, seznam_2)
print("deljenje dveh seznamov z / in z np.divide():\n", rez_deljenje_1,"\n", rez_deljenje_2)
# deljenje seznama s skalarjem
rez_deljenje_3 = seznam_1 / skalar
rez_deljenje_4 = np.divide(seznam_1, skalar)
print("deljenje seznama s skalarjem z / in z np.divide():\n", rez_deljenje_3,"\n", rez_deljenje_4)
# deljenje skalarja s seznamom
rez_deljenje_5 = skalar / seznam_1
rez_deljenje_6 = np.divide(skalar, seznam_1)
print("deljenje skalarja s seznamom z / in z np.divide():\n", rez_deljenje_5,"\n", rez_deljenje_6)
# potenciranje dveh seznamov
rez_potenciranje_1 = seznam_1 ** seznam_2
rez_potenciranje_2 = np.power(seznam_1, seznam_2)
print("potenciranje dveh seznamov z ** in z np.power():\n", rez_potenciranje_1,"\n", rez_potenciranje_2)
# potenciranje seznama s skalarjem
rez_potenciranje_3 = seznam_1 ** skalar
rez_potenciranje_4 = np.power(seznam_1, skalar)
print("potenciranje seznama s skalarjem z ** in z np.power():\n", rez_potenciranje_3,"\n", rez_potenciranje_4)
# potenciranje skalarja s seznamom
rez_potenciranje_5 = skalar ** seznam_1
rez_potenciranje_6 = np.power(skalar, seznam_1)
print("potenciranje skalarja s seznamom z ** in z np.power():\n", rez_potenciranje_5,"\n", rez_potenciranje_6)
# modulus dveh seznamov
rez_modulus_1 = seznam_1 % seznam_2
rez_modulus_2 = np.mod(seznam_1, seznam_2)
print("modulus dveh seznamov z % in z np.mod():\n", rez_modulus_1,"\n", rez_modulus_2)
# modulus seznama s skalarjem
rez_modulus_3 = seznam_1 % skalar
rez_modulus_4 = np.mod(seznam_1, skalar)
print("modulus seznama s skalarjem z % in z np.mod():\n", rez_modulus_3,"\n", rez_modulus_4)
# modulus skalarja s seznamom
rez_modulus_5 = skalar % seznam_1
rez_modulus_6 = np.mod(skalar, seznam_1)
print("modulus skalarja s seznamom z % in z np.mod():\n", rez_modulus_5,"\n", rez_modulus_6)
############
# 2D seznami
############
print("#"*10)
print("2D seznami")
print("#"*10)
seznam_1 = np.array([[1, 2, 3, 4],[5, 6, 7, 8]])
seznam_2 = np.array([[1, 2, 1, 2],[3, 4, 3, 4]])
skalar = 3
print("seznam_1\n", seznam_1)
print("seznam_2\n", seznam_2)
print("skalar\n", skalar)
# seštevanje dveh seznamov
rez_seštevanje_1 = seznam_1 + seznam_2
rez_seštevanje_2 = np.add(seznam_1, seznam_2)
print("seštevanje dveh seznamov s + in z np.add():\n", rez_seštevanje_1,"\n", rez_seštevanje_2)
# seštevanje seznama s skalarjem
rez_seštevanje_3 = seznam_1 + skalar
rez_seštevanje_4 = np.add(seznam_1, skalar)
print("seštevanje seznama s skalarjem s + in z np.add():\n", rez_seštevanje_3,"\n", rez_seštevanje_4)
# odštevanje dveh seznamov
rez_odštevanje_1 = seznam_1 - seznam_2
rez_odštevanje_2 = np.subtract(seznam_1, seznam_2)
print("odštevanje dveh seznamov z - in z np.subtract():\n", rez_odštevanje_1,"\n", rez_odštevanje_2)
# odštevanje seznama s skalarjem
rez_odštevanje_3 = seznam_1 - skalar
rez_odštevanje_4 = np.subtract(seznam_1, skalar)
print("odštevanje seznama s skalarjem z - in z np.subtract():\n", rez_odštevanje_3,"\n", rez_odštevanje_4)
# množenje dveh seznamov
rez_množenje_1 = seznam_1 * seznam_2
rez_množenje_2 = np.multiply(seznam_1, seznam_2)
print("množenje dveh seznamov z * in z np.multiply():\n", rez_množenje_1,"\n", rez_množenje_2)
# množenje seznama s skalarjem
rez_množenje_3 = seznam_1 * skalar
rez_množenje_4 = np.multiply(seznam_1, skalar)
print("množenje seznama s skalarjem z * in z np.multiply():\n", rez_množenje_3,"\n", rez_množenje_4)
# deljenje dveh seznamov
rez_deljenje_1 = seznam_1 / seznam_2
rez_deljenje_2 = np.divide(seznam_1, seznam_2)
print("deljenje dveh seznamov z / in z np.divide():\n", rez_deljenje_1,"\n", rez_deljenje_2)
# deljenje seznama s skalarjem
rez_deljenje_3 = seznam_1 / skalar
rez_deljenje_4 = np.divide(seznam_1, skalar)
print("deljenje seznama s skalarjem z / in z np.divide():\n", rez_deljenje_3,"\n", rez_deljenje_4)
# deljenje skalarja s seznamom
rez_deljenje_5 = skalar / seznam_1
rez_deljenje_6 = np.divide(skalar, seznam_1)
print("deljenje skalarja s seznamom z / in z np.divide():\n", rez_deljenje_5,"\n", rez_deljenje_6)
# potenciranje dveh seznamov
rez_potenciranje_1 = seznam_1 ** seznam_2
rez_potenciranje_2 = np.power(seznam_1, seznam_2)
print("potenciranje dveh seznamov z ** in z np.power():\n", rez_potenciranje_1,"\n", rez_potenciranje_2)
# potenciranje seznama s skalarjem
rez_potenciranje_3 = seznam_1 ** skalar
rez_potenciranje_4 = np.power(seznam_1, skalar)
print("potenciranje seznama s skalarjem z ** in z np.power():\n", rez_potenciranje_3,"\n", rez_potenciranje_4)
# potenciranje skalarja s seznamom
rez_potenciranje_5 = skalar ** seznam_1
rez_potenciranje_6 = np.power(skalar, seznam_1)
print("potenciranje skalarja s seznamom z ** in z np.power():\n", rez_potenciranje_5,"\n", rez_potenciranje_6)
# modulus dveh seznamov
rez_modulus_1 = seznam_1 % seznam_2
rez_modulus_2 = np.mod(seznam_1, seznam_2)
print("modulus dveh seznamov z % in z np.mod():\n", rez_modulus_1,"\n", rez_modulus_2)
# modulus seznama s skalarjem
rez_modulus_3 = seznam_1 % skalar
rez_modulus_4 = np.mod(seznam_1, skalar)
print("modulus seznama s skalarjem z % in z np.mod():\n", rez_modulus_3,"\n", rez_modulus_4)
# modulus skalarja s seznamom
rez_modulus_5 = skalar % seznam_1
rez_modulus_6 = np.mod(skalar, seznam_1)
print("modulus skalarja s seznamom z % in z np.mod():\n", rez_modulus_5,"\n", rez_modulus_6)
########## 1D seznami ########## seznam_1 [1 2 3 4] seznam_2 [5 6 7 8] skalar 3 seštevanje dveh seznamov s + in z np.add(): [ 6 8 10 12] [ 6 8 10 12] seštevanje seznama s skalarjem s + in z np.add(): [4 5 6 7] [4 5 6 7] odštevanje dveh seznamov z - in z np.subtract(): [-4 -4 -4 -4] [-4 -4 -4 -4] odštevanje seznama s skalarjem z - in z np.subtract(): [-2 -1 0 1] [-2 -1 0 1] množenje dveh seznamov z * in z np.multiply(): [ 5 12 21 32] [ 5 12 21 32] množenje seznama s skalarjem z * in z np.multiply(): [ 3 6 9 12] [ 3 6 9 12] deljenje dveh seznamov z / in z np.divide(): [0.2 0.33333333 0.42857143 0.5 ] [0.2 0.33333333 0.42857143 0.5 ] deljenje seznama s skalarjem z / in z np.divide(): [0.33333333 0.66666667 1. 1.33333333] [0.33333333 0.66666667 1. 1.33333333] deljenje skalarja s seznamom z / in z np.divide(): [3. 1.5 1. 0.75] [3. 1.5 1. 0.75] potenciranje dveh seznamov z ** in z np.power(): [ 1 64 2187 65536] [ 1 64 2187 65536] potenciranje seznama s skalarjem z ** in z np.power(): [ 1 8 27 64] [ 1 8 27 64] potenciranje skalarja s seznamom z ** in z np.power(): [ 3 9 27 81] [ 3 9 27 81] modulus dveh seznamov z % in z np.mod(): [1 2 3 4] [1 2 3 4] modulus seznama s skalarjem z % in z np.mod(): [1 2 0 1] [1 2 0 1] modulus skalarja s seznamom z % in z np.mod(): [0 1 0 3] [0 1 0 3] ########## 2D seznami ########## seznam_1 [[1 2 3 4] [5 6 7 8]] seznam_2 [[1 2 1 2] [3 4 3 4]] skalar 3 seštevanje dveh seznamov s + in z np.add(): [[ 2 4 4 6] [ 8 10 10 12]] [[ 2 4 4 6] [ 8 10 10 12]] seštevanje seznama s skalarjem s + in z np.add(): [[ 4 5 6 7] [ 8 9 10 11]] [[ 4 5 6 7] [ 8 9 10 11]] odštevanje dveh seznamov z - in z np.subtract(): [[0 0 2 2] [2 2 4 4]] [[0 0 2 2] [2 2 4 4]] odštevanje seznama s skalarjem z - in z np.subtract(): [[-2 -1 0 1] [ 2 3 4 5]] [[-2 -1 0 1] [ 2 3 4 5]] množenje dveh seznamov z * in z np.multiply(): [[ 1 4 3 8] [15 24 21 32]] [[ 1 4 3 8] [15 24 21 32]] množenje seznama s skalarjem z * in z np.multiply(): [[ 3 6 9 12] [15 18 21 24]] [[ 3 6 9 12] [15 18 21 24]] deljenje dveh seznamov z / in z np.divide(): [[1. 1. 3. 2. ] [1.66666667 1.5 2.33333333 2. ]] [[1. 1. 3. 2. ] [1.66666667 1.5 2.33333333 2. ]] deljenje seznama s skalarjem z / in z np.divide(): [[0.33333333 0.66666667 1. 1.33333333] [1.66666667 2. 2.33333333 2.66666667]] [[0.33333333 0.66666667 1. 1.33333333] [1.66666667 2. 2.33333333 2.66666667]] deljenje skalarja s seznamom z / in z np.divide(): [[3. 1.5 1. 0.75 ] [0.6 0.5 0.42857143 0.375 ]] [[3. 1.5 1. 0.75 ] [0.6 0.5 0.42857143 0.375 ]] potenciranje dveh seznamov z ** in z np.power(): [[ 1 4 3 16] [ 125 1296 343 4096]] [[ 1 4 3 16] [ 125 1296 343 4096]] potenciranje seznama s skalarjem z ** in z np.power(): [[ 1 8 27 64] [125 216 343 512]] [[ 1 8 27 64] [125 216 343 512]] potenciranje skalarja s seznamom z ** in z np.power(): [[ 3 9 27 81] [ 243 729 2187 6561]] [[ 3 9 27 81] [ 243 729 2187 6561]] modulus dveh seznamov z % in z np.mod(): [[0 0 0 0] [2 2 1 0]] [[0 0 0 0] [2 2 1 0]] modulus seznama s skalarjem z % in z np.mod(): [[1 2 0 1] [2 0 1 2]] [[1 2 0 1] [2 0 1 2]] modulus skalarja s seznamom z % in z np.mod(): [[0 1 0 3] [3 3 3 3]] [[0 1 0 3] [3 3 3 3]]
3.2. Kotne funkcije
V spodnji tabeli so navedene najbolj pogosto uporabljene kotne funkcije v knjižnici numpy.
Kotne funkcije |
Opis |
|
Izračuna sinus kota podanega v radianih. |
|
Izračuna kosinus kota podanega v radianih. |
|
Izračuna tangens kota podanega v radianih. |
|
Izračuna inverz sinusa. |
|
Izračuna inverz kosinusa. |
|
Izračuna inverz tangensa. |
|
Pretvori kot iz radianov v stopinje. |
|
Pretvori kot iz stopinj v radiane. |
Podobno kot ostale funkcije v knjižnici, tudi kotne funkcije delujejo na celotnem seznamu. Na primer kosinuse za seznam izračunamo kot:
koti = np.array([0, 1, 2]) kosinusi = np.cos(koti) print(kosinusi) # izpis: [1. 0.54030231 -0.41614684]
kjer je potrebno paziti, da kote podajamo v radianih.
|
Pri kotnih funkcijah |
Če bi radi iz vrednosti kosinusov dobili vrednosti kotov, to naredimo z inverzno funkcijo np.arccos():
vrednosti_kotov = np.arccos(kosinusi) print(vrednosti_kotov) # izpis: [0. 1. 2.]
V pomoč pri pretvorbi med radiani in stopinjami je funkcija np.degrees(), ki pretvori vrednost kotov iz radianov v stopinje:
koti_stopinje = np.degrees(koti) print(koti_stopinje) # izpis: [0. 57.29577951 114.59155903]
V obratni smeri lahko uporabimo funkcijo np.radians(), ki pretvori vrednosti kotov iz stopinj v radiane:
koti_radiani = np.radians(koti_stopinje) print(koti_radiani) # izpis: [0. 1. 2.]
3.2.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Kotne funkcije. Rešitve nalog najdete v razdelku Rešitve.
-
Definiraj seznam kotov v stopinjah z naslednjimi vrednostmi: 0, 15, 30, 45, 60, 90, 270, 360.
-
Pretvori kote v radiane.
-
pretvori kote nazaj v stopinje.
-
Določi sinuse kotov.
-
Določi inverze sinusov.
-
Določi kosinuse kotov.
-
Določi inverze kosinusov.
-
Preveri, če za poljuben kot \(a\) velja \(sin(a)^2 + cos(a)^2 = 1\).
-
Določi tangense kotov.
-
Določi inverze tangensov.
3.2.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
# seznam kotov v stopinjah
koti_stopinje = np.array([0, 15, 30, 45, 60, 90, 270, 360])
print("koti_stopinje\n", koti_stopinje)
# pretvorba kotov v radiane
koti_radiani = np.radians(koti_stopinje)
print("koti_radiani\n", koti_radiani)
#pretvorba iz radianov v stopinje
koti_stopinje2 = np.degrees(koti_radiani)
print("koti_stopinje2\n", koti_stopinje2)
# izračun sinusov
vrednosti_sin = np.sin(koti_radiani)
print("sinusi\n", vrednosti_sin)
#izračun arcsin
vrednosti_arcsin = np.arcsin(vrednosti_sin)
print("vrednosti_arcsin\n", vrednosti_arcsin)
# izračun kosinusov
vrednosti_cos = np.cos(koti_radiani)
print("sinusi\n", vrednosti_cos)
#izračun arccos
vrednosti_arccos = np.arccos(vrednosti_cos)
print("vrednosti_arccos\n", vrednosti_arccos)
# preverimo če velja sin(alfa) ** 2 + cos(alfa) ** 2 = 1
vsota_kvadratov = vrednosti_cos ** 2 + vrednosti_sin ** 2
print("vsota_kvadratov\n", vsota_kvadratov)
# izračun tangensov
vrednosti_tan = np.tan(koti_radiani)
print("vrednosti_tan\n", vrednosti_tan)
#izračun arctan
vrednosti_arctan = np.arctan(vrednosti_tan)
print("vrednosti_arctan\n", vrednosti_arctan)
koti_stopinje [ 0 15 30 45 60 90 270 360] koti_radiani [0. 0.26179939 0.52359878 0.78539816 1.04719755 1.57079633 4.71238898 6.28318531] koti_stopinje2 [ 0. 15. 30. 45. 60. 90. 270. 360.] sinusi [ 0.00000000e+00 2.58819045e-01 5.00000000e-01 7.07106781e-01 8.66025404e-01 1.00000000e+00 -1.00000000e+00 -2.44929360e-16] vrednosti_arcsin [ 0.00000000e+00 2.61799388e-01 5.23598776e-01 7.85398163e-01 1.04719755e+00 1.57079633e+00 -1.57079633e+00 -2.44929360e-16] sinusi [ 1.00000000e+00 9.65925826e-01 8.66025404e-01 7.07106781e-01 5.00000000e-01 6.12323400e-17 -1.83697020e-16 1.00000000e+00] vrednosti_arccos [0. 0.26179939 0.52359878 0.78539816 1.04719755 1.57079633 1.57079633 0. ] vsota_kvadratov [1. 1. 1. 1. 1. 1. 1. 1.] vrednosti_tan [ 0.00000000e+00 2.67949192e-01 5.77350269e-01 1.00000000e+00 1.73205081e+00 1.63312394e+16 5.44374645e+15 -2.44929360e-16] vrednosti_arctan [ 0.00000000e+00 2.61799388e-01 5.23598776e-01 7.85398163e-01 1.04719755e+00 1.57079633e+00 1.57079633e+00 -2.44929360e-16]
3.3. Ostale matematične funkcije
V spodnji tabeli so navedene preostale pogosto uporabljene matematične funkcije v knjižnici numpy.
Funkcije |
Opis |
|
Izračuna produkt vseh elementov v seznamu. |
|
Izračuna vsoto vseh elementov v seznamu. |
|
Izračuna naravno eksponentno funkcijo za vsak element. |
|
Izračuna naravna logaritem za vsak element. |
|
Izračuna logaritem z osnovo 10 za vsak element. |
|
Izračuna logaritem z osnovo 2 za vsak element. |
|
Izračuna kvadratni koren za vsak element. |
|
Izračuna kubični koren za vsak element. |
|
Izračuna absolutno vrednost za vsak element. |
|
Izračuna predznak za vsak element. |
Večina zornjih funkcije deluje na posameznem elementu v seznamu. Drugače delujeta le funkciji np.prod() in np.sum(), ki vrneta eno vrednost za celoten seznam. Na primer:
seznam = np.array([0, 1, 2]) vsota = np.sum(seznam) print(vsota) # izpis: 3
izračuna vsoto vseh elementov v seznamu.
Vse preostale funkcije izračunajo vrednost za vsak element posebej. Na primer:
seznam = np.array([0, 1, 2]) koreni = np.sqrt(seznam) print(koreni) # izpis: [0. 1. 1.41421356]
izračuna kvadratni koren za vsak element posebej.
3.3.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljeni v razdelku Ostale matematične funkcije. Rešitve nalog najdete v razdelku Rešitve.
-
Pripravi seznam
seznam_1D, ki vsebuje 5 naključnih števil. -
Pripravi seznam
seznam_2D, ki ima 2 vrstici in 3 stolpce in vsebuje poljubna števila določena z normalno porazdelitvijo. -
Določi produkt vseh elementov seznama
seznam_1D. -
Določi vsoto vseh elementov seznama
seznam_2D. -
Izračunaj vrednosti eksponentne funkcije za elemente seznama
seznam_1D. -
Izračunaj naravni logaritem za elemente seznama
seznam_2D. -
Izračunaj logaritem z osnovo 10 za elemente seznama
seznam_1D. -
Izračunaj logaritem z osnovo 2 za elemente seznama
seznam_1D. -
Izračunaj kvadratni koren za elemente seznama
seznam_1D. -
izračunaj kubični koren za elemente seznama
seznam_2D. -
Izračunaj absolutne vrednosti elementov seznama
seznam_2D. -
Izračunaj predznake elementov seznama
seznam_1D.
3.3.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import numpy as np
# definicija seznamov
seznam_1D = np.random.rand(5)
print("seznam_1D", seznam_1D)
seznam_2D = np.random.randn(2,3)
print("seznam_2D", seznam_2D)
# produkt vseh elementov
rezultat_prod = np.prod(seznam_1D)
print("rezultat_prod",rezultat_prod)
# vsota vseh elementov
rezultat_sum = np.sum(seznam_2D)
print("rezultat_sum",rezultat_sum)
# naravna eksponentna funkcija po elementih
rezultat_exp = np.exp(seznam_1D)
print("rezultat_exp",rezultat_exp)
# naravna logaritem po elementih
rezultat_log = np.log(seznam_1D)
print("rezultat_log",rezultat_log)
# logaritem z osnovo 10 po elementih
rezultat_log10 = np.log10(seznam_1D)
print("rezultat_log10",rezultat_log10)
# logaritem z osnovo 2 po elementih
rezultat_log2 = np.log2(seznam_1D)
print("rezultat_log2",rezultat_log2)
# kvadratni koren po elementih
rezultat_sqrt = np.sqrt(seznam_1D)
print("rezultat_sqrt",rezultat_sqrt)
# kubični koren po elementih
rezultat_cbrt = np.cbrt(seznam_2D)
print("rezultat_cbrt",rezultat_cbrt)
# absolutna vrednost po elementih
rezultat_absolute = np.absolute(seznam_2D)
print("rezultat_absolute",rezultat_absolute)
# predznak po elementih
rezultat_sign = np.sign(seznam_1D)
print("rezultat_sign",rezultat_sign)
seznam_1D [0.15045323 0.46157697 0.54943333 0.50234396 0.09848053] seznam_2D [[-0.54018629 -0.94752376 1.18359164] [-0.20011211 0.77969094 -0.6332221 ]] rezultat_prod 0.0018876097941248652 rezultat_sum -0.357761661515104 rezultat_exp [1.16236094 1.58657399 1.73227112 1.65259033 1.10349292] rezultat_log [-1.89410302 -0.77310646 -0.59886783 -0.68847022 -2.31789637] rezultat_log10 [-0.82259849 -0.33575587 -0.260085 -0.29899882 -1.0066496 ] rezultat_log2 [-2.73261303 -1.11535686 -0.86398365 -0.99325258 -3.3440176 ] rezultat_sqrt [0.38788301 0.67939456 0.7412377 0.70876227 0.31381608] rezultat_cbrt [[-0.81441891 -0.9821927 1.05779286] [-0.58491279 0.92039481 -0.85872087]] rezultat_absolute [[0.54018629 0.94752376 1.18359164] [0.20011211 0.77969094 0.6332221 ]] rezultat_sign [1. 1. 1. 1. 1.]
3.4. Matrične operacije
3.4.1. Matrični in vektorski produkti
Knjižnica numpy ponuja vrsto različnih matričnih in vektorskih operacij. Najpomembnejše, iz inženirskega stališča, so navedene v spodnji tabeli.
Funkcija |
Opis |
|
Produkt dveh matrik. |
|
Produkt dveh ali več matrik. |
|
Skalarni produkt dveh vektorjev. |
|
Izračuna inverz (obrnljive) matrike. |
Za produkt spodnjih dveh matrik:
matrika_1 = np.array([[1, 2], [3, 4]]) matrika_2 = np.array([[5, 6], [7, 8]])
lahko uporabimo funkciji np.dot():
rezultat_dot = np.dot(matrika_1, matrika_2)
ki nam vrne seznam oblike:
[[19 22] [43 50]]
V kolikor bi radi izvrednotili produkt večih matrik, lahko večkrat uporabimo funkcijo np.dot(), ali pa uporabimo funkcijo np.linalg.multi_dot(), ki z enim ukazom izvrednoti večkratno operacijo. Na primer:
rezultat_multi_dot = np.linalg.multi_dot((matrika_1,matrika_2,matrika_1))
vrne naslednjo matriko:
[[ 85 126] [193 286]]
V primeru dveh vektorjev:
vektor_1 = np.array([1, 2, 3, 4]) vektor_2 = np.array([5, 6, 7, 8])
lahko za skalarni produkt uporabimo funkcijo np.dot() ali pa funkcijo np.vdot():
rezultat_dot = np.vdot(vektor_1, vektor_2) rezultat_vdot = np.vdot(vektor_1, vektor_2)
kjer za zgornji primer obe funkciji vrneta vrednost 70.
Inverze matrik določimo s funkcijo np.linalg.inv(). Na primer matriko matrika_1 lahko obrnemo z naslednjo programsko kodo:
inverz_marika_1 = np.linalg.inv(matrika_1)
kjer je rezultat oblike:
[[-2. 1.] [1.5 -0.5]]
3.4.2. Norme in druge lastnosti matrik
V spodnji tabeli so povzete funkcije, s katerimi določimo najpomembnejše lastnosti matrik.
Funkcija |
Opis |
|
Izračun matrične ali vektorske norme. |
|
Izračun determinante matrike. |
|
Izračun ranga matrike. |
|
Izračun sledi matrike. |
Spodnji matriki:
matrika = np.array([[1, 2], [3, 4]])
lahko določimo matrično normo:
norma_matrike = np.linalg.norm(matrika) print(norma_matrike) # izpis: 5.477225575051661
njeno determinanto:
determinanta_matrike = np.linalg.det(matrika) print(determinanta_matrike) # izpis: -2.0000000000000004
rang matrike:
rang_matrike = np.linalg.matrix_rank(matrika) print(rang_matrike) # izpis: 2
in sled matrike:
sled_matrike = np.trace(matrika) print(sled_matrike) # izpis: 5
3.4.3. Lastne vrednosti matrik
Za določitev lastnih vrednosti in lastnih vektorjev matrik se uporabljata naslednji funkciji.
Funkcija |
Opis |
|
Izračun lastnih vrednosti in lastnih vektorjev kvadratne matrike. |
|
Izračun lastnih vrednosti matrike. |
Funkcija np.linalg.eig() vrne tako lastne vrednosti kakor tudi lastne vektorje matrike. Na primer:
matrika = np.array([[1, 2], [3, 4]]) rezultat_eig = np.linalg.eig(matrika)
kjer je rezultat naslednje oblike:
(array([-0.37228132, 5.37228132]),
array([[-0.82456484, -0.41597356],
[ 0.56576746, -0.90937671]]))
Funkcija np.linalg.eigvals() pa vrne le lastne vrednosti:
rezultat_eigvals = np.linalg.eigvals(matrika) print(rezultat_eigvals) # izpis: [-0.37228132 5.37228132]
3.4.4. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Matrične operacije. Rešitve nalog najdete v razdelku Rešitve.
-
Definiraj seznam
napetosti, v katerega shraniš napetostni tenzor [[1, 0, 0], [0, 3, -1], [0, -1, 3]]. -
Določi in izpiši normo napetostnega tenzorja
norma. -
Določi in izpiši determinanto napetostnega tenzorja
determinanta. -
Določi in izpiši rang napetostnega tenzorja
rang. -
Določi in izpiši sled napetostnega tenzorja
sled. -
Določi in izpiši lastne vrednosti in lastne vektorje napetostnega tenzorja, vrednosti shrani v seznam
vrednosti, vektorje pa v seznamvektorji. -
S funkcijo
np.diag()definiraj in izpiši matrikonapetosti_glavne, ki po diagonali vsebuje lastne vrednosti napetostnega tenzorja. -
Določi matriko
napetosti_glavne_2, ki jo izračunaš kot(vektorji^(-1)).napetost.vektorjiin preveri, ali je enaka kot matrikanapetosti_glavne.
3.4.5. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
# tenzor napetosti
napetost = np.array([[1, 0, 0], [0, 3, -1], [0, -1, 3]])
# norma
norma = np.linalg.norm(napetost)
print("norma:", norma)
# determinanta
determinanta = np.linalg.det(napetost)
print("determinanta:", determinanta)
# rang
rang = np.linalg.matrix_rank(napetost)
print("rang:", rang)
# sled
sled = np.trace(napetost)
print("sled:", sled)
#lastne vrednosti in vektorji
vrednosti, vektorji = np.linalg.eig(napetost)
print("lastne vrednosti:", vrednosti)
print("lastni vektorji:\n", vektorji)
#diagonalna matrika
napetosti_glavne = np.diag(vrednosti)
print("napetosti_glavne:\n", napetosti_glavne)
#diagonalno matrika s transofrmacijo
napetosti_glavne_2 = np.linalg.multi_dot((np.linalg.inv(vektorji), napetost, vektorji))
print("napetosti_glavne_2:\n", napetosti_glavne_2)
norma: 4.58257569495584 determinanta: 8.000000000000002 rang: 3 sled: 7 lastne vrednosti: [4. 2. 1.] lastni vektorji: [[ 0. 0. 1. ] [-0.70710678 0.70710678 0. ] [ 0.70710678 0.70710678 0. ]] napetosti_glavne: [[4. 0. 0.] [0. 2. 0.] [0. 0. 1.]] napetosti_glavne_2: [[ 4.00000000e+00 -2.02930727e-17 0.00000000e+00] [-4.05861454e-17 2.00000000e+00 0.00000000e+00] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
Poglavje 4. Dodatne funkcionalnosti
4.1. Reševanje enačb
Pri reševanju sistemov linarnih enačb si lahko pomagamo s spodnjimi funkcijami.
Funkcija |
Opis |
|
Poišče vektor x za linearni sistem enačb |
|
Izračuna inverz (obrnljive) matrike. |
|
Poišče vektor x, ki po metodi najmanjših kvadratov najbolj ustreza sistemu enačb |
Sistemu linearnih enačb, ki je določen z matriko A = np.array[[1, 2], [3, 4]] in vektorjem desnih strani b = np.array([5, 6]) lahko najdemo rešitev z uporabo funkcije np.linalg.solve():
x = np.linalg.solve(A,b) print(x) # izpis: [-4. 4.5]
Zgornji sistem lahko rešimo tudi posredno z uporabo inverzne matrike z uporabo funkcije np.linalg.inv():
invA = np.linalg.inv(A) print(invA) # izpis: [[-2. 1. ] [ 1.5 -0.5]] x2 = np.dot(invA,b) print(x2) # izpis: [-4. 4.5]
Pri predoločenih sistemih enačb oziroma v primerih, ko bi radi skozi izbrane točke priredili linearno funkcijo, uporabimo funkcijo np.linalg.lstsq(), ki najde rešitev po metodi najmanjših kvadatov. Na primer:
A = np.array([[1, 2], [3, 4], [5, 6]]) b = np.array([7, 8, 9]) x = np.linalg.lstsq(A, b, rcond=None)[0] # izpis: [-6. 6.5] print(x)
4.1.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Reševanje enačb. Rešitve nalog najdete v razdelku Rešitve.
-
Zapiši dani sistem enačb \(x + y + z = 1, 4x + 2y = 6, x + 4y + z = 2\) v obliki \(A.X=b\), kjer je
Amatrika koeficientov,Xje vektor neznank,bpa vektor desnih strani. -
Določi vektor neznank
Xz uporabo inverzne matrike. -
Določi vektor neznank
Xneposredno z uporabo funkcije np.linalg.solve(). -
Za dani sistem enačb \(x + 2y + z = −1, x + 3y + 2z = 2, 2x + 5y + 3z = 0, 2x + z = 1, 3x + y + z = −2\) najdi rešitev po metodi najmanjših kvadratov.
|
Naloge so povzete iz Domače vaje iz LINEARNE ALGEBRE, Marjeta Kramar Fijavž, Fakulteta za gradbeništvo in geodezijo Univerze v Ljubljani, 2007/08, kjer lahko najdete še več podobnih nalog. |
4.1.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
# matrika koeficientov
A = np.array([[1, 1, 1], [4, 2, 0], [1, 4, 1]])
print("A\n", A)
# desne strani
b = np.array([1, 6, 2])
print("b\n", b)
#inverz A
invA = np.linalg.inv(A)
print("invA\n", invA)
# rešitev z inverzom
X = np.dot(invA,b)
print("rešitev X z inverzom", X)
# rešitev neposredno
X = np.linalg.solve(A,b)
print("rešitev neposredno", X)
# matrika koeficientov
A1 = np.array([[1, 2, 1], [1, 3, 2], [2, 5, 3], [2, 0, 1], [3, 1, 1]])
print("A1\n", A1)
# desne strani
b1 = np.array([-1, 2, 0, 1, -2])
print("b1\n", b1)
# rešitev po metodi najmanjših kvadratov
X1 = np.linalg.lstsq(A1, b1, rcond=None)[0]
print("rešitev X1 po metodi najmanjših kvadratov", X1)
A [[1 1 1] [4 2 0] [1 4 1]] b [1 6 2] invA [[ 0.16666667 0.25 -0.16666667] [-0.33333333 0. 0.33333333] [ 1.16666667 -0.25 -0.16666667]] rešitev X z inverzom [ 1.33333333 0.33333333 -0.66666667] rešitev neposredno [ 1.33333333 0.33333333 -0.66666667] A1 [[1 2 1] [1 3 2] [2 5 3] [2 0 1] [3 1 1]] b1 [-1 2 0 1 -2] rešitev X1 po metodi najmanjših kvadratov [-1.53333333 -1.86666667 4.26666667]
4.2. Zaokroževanje
Funkcije zaokroževanja uporabljamo za zaokroževanje elementov v seznamih na določeno natančnost oziroma na določeno število decimalnih mest.
V spodnji tabeli so navedene najpogosteje uporabljene zaokrožitvene funkcije.
| Funkcija | Opis |
|---|---|
|
Za vsak element v seznamu vrne vrednost zaokroženo na željeno natančnost (decimalno mesto). |
|
Za vsak element v seznamu vrne najbližje celo število, ki je manjše od vrednosti elementa. |
|
Za vsak element v seznamu vrne najbližje celo število, ki je večje od vrednosti elementa. |
S funkcijo np.round() lahko zaokrožimo elemente seznama na željeno natančnost. Na primer spodnja programska koda:
stevila = np.array([1.1111, 2.2222, 3.3333, 4.4444]) stevila_1 = np.round(stevila, 1) print(stevila_1) # izpis: [1.1 2.2 3.3 4.4]
zaokroži vrednosti na 1 decimalno mesto.
S fukncijo np.floor() zaokrožujemo navzdol:
stevila_dol = np.floor(stevila) print(stevila_dol) # izpis: [1. 2. 3. 4.]
ter s funkcijo np.ceil() zaokrožujemo navzgor:
stevila_gor = np.ceil(stevila) print(stevila_gor) # izpis: [2. 3. 4. 5.]
4.2.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Zaokroževanje. Rešitve nalog najdete v razdelku Rešitve.
-
Pripravi seznam, ki vsebuje naslednje vrednosti 1.111, 2.222, 3.333, 4.444, 5.555, 6.666.
-
Zaokroži vrednosti elementov seznama na cela števila in izpiši seznam.
-
Zaokroži vrednosti elementov seznama na 2 decimalni mesti in izpiši seznam.
-
Zaokroži vrednosti elementov seznama na 1 decimalno mesto in izpiši seznam.
-
Zaokroži vrednosti elementov seznama navzdol in izpiši seznam.
-
Zaokroži vrednosti elementov seznama navzgor in izpiši seznam.
4.2.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
seznam = np.array([1.111, 2.222, 3.333, 4.444, 5.555, 6.666])
# zaokrožitev na cela števila
seznam_round = np.round(seznam)
print("seznam_round\n", seznam_round)
seznam_round0 = np.round(seznam, 0)
print("seznam_round0\n", seznam_round0)
# zaokrožitev na 2 decimalni mesti
seznam_round2 = np.round(seznam, 2)
print("seznam_round2\n", seznam_round2)
# zaokrožitev na 1 decimalno mesto
seznam_round1 = np.round(seznam, 1)
print("seznam_round1\n", seznam_round1)
# zaokrožitev navzdol
seznam_floor = np.floor(seznam)
print("seznam_floor\n", seznam_floor)
# zaokrožitev navzgor
seznam_ceil = np.ceil(seznam)
print("seznam_ceil\n", seznam_ceil)
original 1D [1 2 3 4] transponiran 1D [1 2 3 4] original 2D [[1 2] [3 4]] transponiran 2D [[1 3] [2 4]] original 3D [[[1 2] [3 4]] [[5 6] [7 8]]] transponiran 3D [[[1 3] [5 7]] [[2 4] [6 8]]]
4.3. Statistika
V spodnji tabeli je navedenih nekaj najpomembnejših statističnih funkcij, ki jih lahko uporabimo pri delu s seznami.
Funkcije |
Opis |
|
Določi mediano (srednjo vrednost) seznama. |
|
Izračuna povprečno vrednost seznama. |
|
Izračuna standarni odklon (standardna deviacija) seznama. |
|
Izračuna željeni percentil seznama. |
|
Določi najmanjšo vrednost v seznamu. |
|
Določi največjo vrednost v seznamu. |
Z uporabo knjižnice numpy lahko za dani seznam vrednosti:
seznam = np.array([0, 0, 1, 1, 3, 5, 6, 8, 9, 9, 3])
določimo mediano oz. srednjo vrednost:
srednja_vrednost = np.median(seznam) print(srednja_vrednost) # izpis: 4.0
povprečje:
povprecje = np.mean(seznam) print(povprecje) # izpis: 4.2
standardni odklon:
std_odklon = np.std(seznam) print(std_odklon) # izpis: 3.4871191548325386
poljuben percentil, npr. v spodnjem primeru 60-it percentil:
percentil_60 = np.percentile(seznam, 60) print(percentil_60) # izpis: 5.3999999999999995
najmanjšo vrednost:
minimum = np.min(seznam) print(minimum) # izpis: 0
ter največjo vrednost:
maksimum = np.max(seznam) print(maksimum) # izpis: 9
Podobno lahko storimo tudi v primeru seznamov višjih dimenzij, kjer imamo še dodatno možnost, da iščemo statistične karkateristike za celoten seznam ali pa za posamezne osi (v primeru 2D seznamov za posamezne stolpce in vrstice). Naslednjemu seznamu:
seznam_2D = np.array([[0, 1, 1, 3, 5], [6, 8, 9, 9, 3]])
lahko določimo npr. standardni odklon z upoštevanjem vseh elementov:
std_odklon = np.std(seznam_2D) print(std_odklon) # izpis: 3.4871191548325386
Z vrednostjo parameta axis=0 povemo, da želimo izračun standardnega odklona v smeri vrstic, kar pomeni, da se izračunajo vrednosti standardnih odklonov za vsak stolpec posebej:
std_odklon_0 = np.std(seznam_2D, axis=0) print(std_odklon_0) # izpis: [3. 3.5 4. 3. 1. ]
Podobno določimo z vrednostjo parametra axis=1 standardne odklone za vsako vrstico posebej:
std_odklon_1 = np.std(seznam_2D, axis=1) print(std_odklon_1) # izpis: [1.78885438 2.28035085]
|
Pri 2D seznamih lahko določimo tudi v kateri smeri naj se izvrši izračun statističnih karkateristik seznama, in sicer:
V kolikor parametra |
4.3.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Statistika. Rešitve nalog najdete v razdelku Rešitve.
-
Pripravi seznam 50-ih naključnih vrednosti porazdeljenih z normalno porazdelitvijo, ki ima srednjo vrednost 50 in standardni odklon 10.
-
Izračunaj in izpiši srednjo vrednost seznama.
-
Izračunaj in izpiši standardni odklon seznama.
-
Izračunaj in izpiši mediano seznama.
-
Izračunaj in izpiši mediano seznama, ki jo določiš z uporabo funkcije ` np.percentile()`.
-
Izračunaj in izpiši 25. percentil seznama.
-
Določi in izpiši najmanjši element seznama.
-
Določi in izpiši največji element seznama.
-
Pripravi seznam, ki je oblike [[1.1, 1.2, 1.3], [3.1, 3.2, 3.3], [7.1, 7.2, 7.3]].
-
Izračunaj in izpiši srednje vrednosti po stolpcih.
-
Izračunaj in izpiši srednje vrednosti po vrsticah.
-
Izračunaj in izpiši srednjo vrednost celotnega seznama.
-
Določi najmanjši element po stolpcih.
-
Določi najmanjši element po vrsticah.
-
Določi najmanjši element celotnega seznama.
4.3.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import numpy as np
# zgeneriramo seznam naključnih vrednosti porazdeljenih z normalno porazdelitvijo
srednja_vrednost = 50
standarni_odklon = 10
seznam = standarni_odklon * np.random.randn(50) + srednja_vrednost
print("seznam\n", seznam)
# izračun srednje vrednosti
seznam_mean = np.mean(seznam)
print("seznam_mean\n", seznam_mean)
# izračun standardnega odklona
seznam_std = np.std(seznam)
print("seznam_std\n", seznam_std)
# izračun mediane
seznam_median = np.median(seznam)
print("seznam_median\n", seznam_median)
# izračun mediane s funcijo percentile()
seznam_median2 = np.percentile(seznam, 50)
print("seznam_median2\n", seznam_median2)
# izračun 25. percentila
seznam_percentile25 = np.percentile(seznam,25)
print("seznam_percentile25\n", seznam_percentile25)
# najmanjši element
seznam_min = np.min(seznam)
print("seznam_min\n", seznam_min)
# največji element
seznam_max = np.max(seznam)
print("seznam_max\n", seznam_max)
# 2d seznam
seznam_2D = np.array([[1.1, 1.2, 1.3],
[3.1, 3.2, 3.3],
[7.1, 7.2, 7.3]])
# izračun srednje vrednosti po stolpcih
seznam_2D_mean0 = np.mean(seznam_2D, axis=0)
print("seznam_2D_mean0\n", seznam_2D_mean0)
# izračun srednje vrednosti po vrsticah
seznam_2D_mean1 = np.mean(seznam_2D, axis=1)
print("seznam_2D_mean1\n", seznam_2D_mean1)
# izračun srednje vrednosti celotnega seznama
seznam_2D_mean = np.mean(seznam_2D)
print("seznam_2D_mean\n", seznam_2D_mean)
# najmanjši element po stolpcih
seznam_2D_min0 = np.min(seznam_2D, axis=0)
print("seznam_2D_min0\n", seznam_2D_min0)
# najmanjši element po vrsticah
seznam_2D_min1 = np.min(seznam_2D, axis=1)
print("seznam_2D_min1\n", seznam_2D_min1)
# najmanjši element celotnega seznama
seznam_2D_min = np.min(seznam_2D)
print("seznam_2D_min\n", seznam_2D_min)
seznam [59.2800862 49.30684234 41.62470762 56.97682666 53.13979494 58.85456065 64.2747638 44.59592954 49.29705586 53.33265949 66.3533084 54.83978799 53.5509975 38.75255501 49.52273936 71.54802576 33.82713275 50.01982414 56.5588116 72.74523797 53.15754208 48.85619429 74.12762058 49.07758449 49.42776782 55.13289532 50.68007113 48.88408253 45.81108793 54.40892332 51.36377012 34.44399323 57.15889533 52.44000641 63.45206393 57.68874462 41.32500471 51.10733731 54.4328317 55.60553245 37.29038252 33.03698385 40.31407382 50.34881937 60.12421208 41.25793222 46.47404492 36.86199348 52.66445084 42.46406997] seznam_mean 51.35641119920799 seznam_std 9.446792237383098 seznam_median 51.23555371494673 seznam_median2 51.23555371494673 seznam_percentile25 45.97682717788532 seznam_min 33.036983849492955 seznam_max 74.12762057542108 seznam_2D_mean0 [3.76666667 3.86666667 3.96666667] seznam_2D_mean1 [1.2 3.2 7.2] seznam_2D_mean 3.8666666666666663 seznam_2D_min0 [1.1 1.2 1.3] seznam_2D_min1 [1.1 3.1 7.1] seznam_2D_min 1.1
4.4. Primerjalni in logični operatorji
Podobno kot v programskem jeziku Python lahko tudi v knjižnici numpy uporabljamo primerjalne in logične operatorje. Edina razlika je v tem, da ponavadi v Python-u primerjamo dve vrednosti medtem ko v numpy primerjamo po dva elementa iz različnih seznamov.
4.4.1. Primerjalni operatorji
S primerjalnimi operatorji primerjamo vrednosti elementov dveh seznamov, kjer je rezultat primerjave nov seznam z logičnimi vrednostmi (True ali False), ki je enakih dimenzij kot seznama, ki ju primerjamo.
V spodnji tabeli so navedeni primerjalni operatorji oziroma primerjalne funkcije v knjižnici numpy.
| Funkcija | Operator | Opis |
|---|---|---|
|
|
Po elementih vrne |
|
|
Po elementih vrne |
|
|
Po elementih vrne |
|
|
Po elementih vrne |
|
|
Po elementih vrne |
|
|
Po elementih vrne |
S primerjalnimi operatorji oziroma primerjalnimi funkcijami lahko primerjamo vrednosti dveh različnih seznamov, kjer pa moramo paziti, da sta oba seznama enakih dimenzij. Če želimo preveriti, kateri elementi v seznamu :
seznam_1 = np.array([1, 2, 3, 4, 5])
so večji ali enaki od elementov v seznamu:
seznam_2 = np.array([5, 4, 3, 2, 1])
lahko to naredimo ali z uporabo operatorja >=:
rezultat_operator = seznam_1 >= seznam_2 print(rezultat_operator) # izpis: [False False True True True]
ali pa z uporabo funkcije np.greater_equal():
rezultat_funkcija = np.greater_equal(seznam_1, seznam_2) print(rezultat_funkcija) # izpis: [False False True True True]
V obeh primerih vidimo, da so 3., 4. in 5. element v seznamu seznam_1 večji od elementov v seznam_2.
Na enak način lahko primerjamo tudi vrednosti med elementi v seznamu in skalarjem:
rezultat_skalar_operator = seznam_1 == 2 print(rezultat_skalar_operator) # izpis: [False True False False False]
kjer smo preverili, kateri elementi v seznamu_1 imajo vrednost 2.
Obnašanje je povsem enako, če uporabimo funkcijo np.equal():
rezultat_skalar_funkcija = np.equal(seznam_1, 2) print(rezultat_skalar_funkcija) # izpis: [False True False False False]
4.4.2. Logične operacije
Logične operacije se izvajajo po elementih, kjer se združuje logične izraze iz dveh seznamov. Rezultat logične operacije je nov seznam z logičnimi vrednostmi, ki je enakih dimenzij kot vhodna seznama.
V spodnji tabeli so navedene logične operacije v knjižnici numpy.
Funkcija |
Opis |
|
Po elementih določi vrednost logične in ( |
|
Po elementih določi vrednost logične ali ( |
|
Po elementih negira ( |
Za dana seznama:
seznam_1 = np.array([False, True, False, True]) seznam_2 = np.array([False, False, True, True])
s funkcijo np.logical_and() izvrednostimo logično in (AND) operacijo po elementih:
rezultat_and = np.logical_and(seznam_1, seznam_2) print(rezultat_and) # Izraz: [False False False True]
kjer se vrednost True v seznamu rezultat_and pojavi le na mestu, kjer imata oba elementa v seznamih seznam_1 in seznam_2 vrednost True.
Podobno lahko s funkcijo np.logical_or() izvrednotimo logično ali (OR) operacijo po elementih:
rezultat_or = np.logical_or(seznam_1, seznam_2) print(rezultat_or) # Izraz: [False True True True]
kjer se vrednost True v seznamu rezultat_or pojavi na mestih, kjer ima vsaj eden od elementov v seznamih seznam_1 in seznam_2 vrednost True.
Logične operacije s funkcijama np.logical_and() in np.logical_or() lahko izvedemo tudi v kombinaciji seznama in posamezne logične vrednosti. Na primer:
rezultat_and_skalar = np.logical_and(seznam_1, True) print(rezultat_and_skalar) # Izraz: [False True False True]
Zadnja logična operacija je negacija (NOT) s funkcijo np.logical_not():
rezultat_not = np.logical_not(seznam_1) print(rezultat_not) # Izraz: [ True False True False]
kjer vidimo, da ima razultat ravno obratne vrednosti kot vhodni seznam.
4.4.3. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Primerjalni in logični operatorji. Rešitve nalog najdete v razdelku Rešitve.
-
Definiraj seznam
seznam_1, ki vsebuje števila od 1 do 50. -
Definiraj seznam
seznam_1, ki vsebuje števila od 76 do 25. -
Določi in izpiši seznam
rezultat_1, ki preveri, ali so elementi vseznam_1večji od elementov vseznam_2. -
Določi in izpiši seznam
rezultat_2, ki preveri, ali so elementi vseznam_1večji ali enaki elementom vseznam_2. -
Izpiši seznam, ki preveri, ali so elementi v
seznam_1manjši od elementov vseznam_2. -
Izpiši seznam, ki preveri, ali so elementi v
seznam_1manjši ali enaki elementom vseznam_2. -
Izpiši seznam, ki preveri, ali so elementi v
seznam_1enaki elementom vseznam_2. -
Izpiši seznam, ki preveri, ali elementi v
seznam_1niso enaki elementom vseznam_2. -
Izpiši seznam, ki po elementih določi logično in (
AND) operacijo za seznamarezultat_1inrezultat_2. -
Izpiši seznam, ki po elementih določi logično ali (
OR) operacijo za seznamarezultat_1inrezultat_2. -
Izpiši seznam, ki negira (
NOT) elemente seznamarezultat_1. -
Definiraj seznam
seznam_3, ki je oblike [[1, 2, …, 10], [11, 12, …, 20], [21, 22, …, 30], [31, 32, …, 40], [41, 42, …, 50]]. -
Definiraj seznam
seznam_4, ki je oblike [[76, 75, …, 67], [66, 65, …, 57], [56, 55, …, 47], [46, 45, …, 37], [36, 35, …, 27]]. -
Določi in izpiši seznam
rezultat_3, ki preveri, ali so elementi vseznam_3večji od elementov vseznam_4. -
Določi in izpiši seznam
rezultat_4, ki preveri, ali so elementi vseznam_3večji ali enaki elementom vseznam_4. -
Izpiši seznam, ki preveri, ali so elementi v
seznam_3manjši od elementov vseznam_4. -
Izpiši seznam, ki preveri, ali so elementi v
seznam_3manjši ali enaki elementom vseznam_4. -
Izpiši seznam, ki preveri, ali so elementi v
seznam_3enaki elementom vseznam_4. -
Izpiši seznam, ki preveri, ali elementi v
seznam_3niso enaki elementom vseznam_4. -
Izpiši seznam, ki po elementih določi logično in (
AND) operacijo za seznamarezultat_3inrezultat_4. -
Izpiši seznam, ki po elementih določi logično ali (
OR) operacijo za seznamarezultat_3inrezultat_4. -
Izpiši seznam, ki negira (
NOT) elemente seznamarezultat_3.
4.4.4. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import numpy as np
# definicija seznamov
seznam_1 = np.arange(1,51)
seznam_2 = np.arange(76,26,-1)
# seznam_1 > seznam_2
rezultat_1 = np.greater(seznam_1, seznam_2)
print("seznam_1 > seznam_2\n", rezultat_1)
# seznam_1 >= seznam_2
rezultat_2 = np.greater_equal(seznam_1, seznam_2)
print("seznam_1 >= seznam_2\n", rezultat_2)
# seznam_1 < seznam_2
print("seznam_1 < seznam_2\n", np.less(seznam_1, seznam_2))
# seznam_1 <= seznam_2
print("seznam_1 <= seznam_2\n", np.less_equal(seznam_1, seznam_2))
# seznam_1 == seznam_2
print("seznam_1 == seznam_2\n", np.equal(seznam_1, seznam_2))
# seznam_1 != seznam_2
print("seznam_1 != seznam_2\n", np.not_equal(seznam_1, seznam_2))
# rezultat_1 AND rezultat_2
print("rezultat_1 AND rezultat_2\n", np.logical_and(rezultat_1, rezultat_2))
# rezultat_1 OR rezultat_2
print("rezultat_1 OR rezultat_2\n", np.logical_or(rezultat_1, rezultat_2))
# NOT rezultat_1
print("rezultat_1 OR rezultat_2\n", np.logical_not(rezultat_1))
# definicija seznamov
seznam_3 = np.array([np.arange(1,11),np.arange(11,21),np.arange(21,31),np.arange(31,41),np.arange(41,51)])
seznam_4 = np.array([np.arange(76,66,-1),np.arange(66,56,-1),np.arange(56,46,-1),np.arange(46,36,-1),np.arange(36,26,-1)])
# seznam_3 > seznam_4
rezultat_3 = seznam_3 > seznam_4
print("seznam_3 > seznam_4\n", seznam_3 > seznam_4)
# seznam_3 >= seznam_4
rezultat_4 = seznam_3 >= seznam_4
print("seznam_3 >= seznam_4\n", seznam_3 >= seznam_4)
# seznam_3 < seznam_4
print("seznam_3 < seznam_4\n", seznam_3 < seznam_4)
# seznam_3 <= seznam_4
print("seznam_3 <= seznam_4\n", seznam_3 <= seznam_4)
# seznam_3 == seznam_4
print("seznam_3 == seznam_4\n", seznam_3 == seznam_4)
# seznam_3 != seznam_4
print("seznam_3 != seznam_4\n", seznam_3 != seznam_4)
# rezultat_3 AND rezultat_4
print("rezultat_3 AND rezultat_4\n", np.logical_and(rezultat_3, rezultat_4))
# rezultat_3 OR rezultat_4
print("rezultat_3 OR rezultat_4\n", np.logical_or(rezultat_3, rezultat_4))
# NOT rezultat_3
print("rezultat_3 OR rezultat_4\n", np.logical_not(rezultat_3))
seznam_1 > seznam_2 [False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False True True True True True True True True True True True True] seznam_1 >= seznam_2 [False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False True True True True True True True True True True True True] seznam_1 < seznam_2 [ True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True False False False False False False False False False False False False] seznam_1 <= seznam_2 [ True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True False False False False False False False False False False False False] seznam_1 == seznam_2 [False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] seznam_1 != seznam_2 [ True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True] rezultat_1 AND rezultat_2 [False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False True True True True True True True True True True True True] rezultat_1 OR rezultat_2 [False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False True True True True True True True True True True True True] rezultat_1 OR rezultat_2 [ True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True True False False False False False False False False False False False False] seznam_3 > seznam_4 [[False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False True True] [ True True True True True True True True True True]] seznam_3 >= seznam_4 [[False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False True True] [ True True True True True True True True True True]] seznam_3 < seznam_4 [[ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True False False] [False False False False False False False False False False]] seznam_3 <= seznam_4 [[ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True False False] [False False False False False False False False False False]] seznam_3 == seznam_4 [[False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False False False]] seznam_3 != seznam_4 [[ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True True True]] rezultat_3 AND rezultat_4 [[False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False True True] [ True True True True True True True True True True]] rezultat_3 OR rezultat_4 [[False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False False False] [False False False False False False False False True True] [ True True True True True True True True True True]] rezultat_3 OR rezultat_4 [[ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True True True] [ True True True True True True True True False False] [False False False False False False False False False False]]
4.5. Logično indeksiranje
Poleg indeksiranja, ki je bilo predstavljeno v razdelku Indeksiranje numpy seznamov, knjižnica numpy omogoča tudi tako imenovano logično indeksiranje.
Poglejmo si, kako deluje logično indeksiranje na seznamu:
seznam = np.array([1, 2, 3, 4, 5, 6, 7, 8])
Recimo, da bi radi iz seznama pobrali le tiste vrednosti, ki so večje od 5. Kot smo pogledali v razdelku Primerjalni in logični operatorji, lahko dobimo sezname z logičnimi vrednostmi True/False z naslednjo programsko kodo:
logicni_indeksi = seznam > 5 print(logicni_indeksi) # izpis: [False False False False False True True True]
Sedaj pa lahko seznam logicni_indeksi uporabimo, da z logičnim indeksiranjem iz seznama seznam dobimo željene vrednosti:
izbrane_vrednosti = seznam[logicni_indeksi] print(izbrane_vrednosti) # izpis: [6 7 8]
Seveda bi lahko to storili tudi neposredno brez uporabe vmesne spremenljivke:
izbrane_vrednosti_neposredno = seznam[seznam > 5] print(izbrane_vrednosti_neposredno) # izpis: [6 7 8]
Logično indeksiranje se lahko uporabi tudi za urejanje seznama:
seznam[logicni_indeksi] = 15 print(seznam) # izpis: [1 2 3 4 5 15 15 15]
V zgornji kodi smo namreč vsem elementom, ki so večji od 5, priredili novo vrednost 15.
Logično indeksiranje deluje tudi v primeru dvo in več dimenzionalnih seznamov.
Sintaksa za določitev logičnih indeksov pri več dimenzionalnih seznamih, npr.:
seznam_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
je povsem identična, kot pri 1D seznamih:
logicni_indeksi_2d = seznam_2d > 5 print(logicni_indeksi_2d) # izpis: [[False False False False] [False True True True] [ True True True True]]
Do razlike pa pride pri rezultatih logičnega indeksiranja. Vsi rezultati, ne glede na dimenzijo vhodnega seznama, so vedno enodimenzionalni.
Tako je tudi v primeru logičnega indeksiranja seznama seznam_2d:
izbrane_vrednosti_2d = seznam_2d[logicni_indeksi_2d] print(izbrane_vrednosti_2d) # izpis: [6 7 8 9 10 11 12]
kjer se določi seznam izbrane_vrednosti_2d, ki je enodimenzionalen.
4.5.1. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Logično indeksiranje. Rešitve nalog najdete v razdelku Rešitve.
-
Določi seznam
seznam, ki vsebuje vrednosti od -10 do 9. -
Določi seznam
lihi_indeksi, ki je enako velik kotseznamin vsebujeTruelogično vrednost na elementih z lihim indeksom. -
Iz seznama
seznamizpiši le elemente, ki so na lihih indeksih. -
Določi seznam
sodi_indeksi, ki je enako velik kotseznamin vsebujeTruelogično vrednost na elementih s sodim indeksom. -
Iz seznama
seznamizpiši le elemente, ki so na sodih indeksih. -
V seznamu
seznamelementom na lihih indeksih popravi vrednost, in sicer v njihove kvadrate. -
Izpiši popravljen seznam
seznam.
4.5.2. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
# definicija seznama
seznam = np.arange(-10,10)
# lihi indeksi
lihi_indeksi = np.arange(0,len(seznam)) % 2 == 1
print("lihi_indeksi\n", lihi_indeksi)
print("vrednosti na lihih indeksih\n", seznam[lihi_indeksi])
#sodi indeksi
sodi_indeksi = np.arange(0,len(seznam)) % 2 == 0
print("sodi_indeksi\n", sodi_indeksi)
print("vrednosti na sodih indeksih\n", seznam[sodi_indeksi])
# kvadriranje elementov na lihih indeksih
seznam[lihi_indeksi] = seznam[lihi_indeksi] ** 2
# popravljen seznam
print("popravljen seznam\n", seznam)
lihi_indeksi [False True False True False True False True False True False True False True False True False True False True] vrednosti na lihih indeksih [-9 -7 -5 -3 -1 1 3 5 7 9] sodi_indeksi [ True False True False True False True False True False True False True False True False True False True False] vrednosti na sodih indeksih [-10 -8 -6 -4 -2 0 2 4 6 8] popravljen seznam [-10 81 -8 49 -6 25 -4 9 -2 1 0 1 2 9 4 25 6 49 8 81]
4.6. Vektorizacija
Vektorizacija s knjižnico numpy omogoča izvedbo matematičnih operacij na celotnem seznamu. Iteriranje po seznamu oziroma uporaba zank je zato odveč.
4.6.1. Primerjava s Python-om
Do sedaj smo se že večkrat srečali z vektorizacijo. Na primer že preposto seštevanje s knjižnico numpy vključuje vektorizacijo:
import numpy as np seznam = np.array([0, 1, 2, 3]) resultat = seznam + 3 print(resultat) # izpis: [3 4 5 6]
kjer se je prištevanje števila 3 izvedlo za vsak element posebej, brez uporabe zanke po elementih.
Poglejmo si, kako bi podoben izračun izgledal v čistem Python-u:
seznam_py = [0, 1, 2, 3]
rezultat_py = []
for element in seznam_py:
rezultat_py.append(element + 3)
print(rezultat_py) # izpis: [3, 4, 5, 6]
V zgornjem primeru vidimo, da je poleg same operacije seštevanja, ki se izvaja za vsak element posebej, potrebno izvesti tudi zanko po vseh elementih. V zgornjem primeru smo za ta namen uporabili zanko for.
|
Omeniti je potrebno, da je pri manjših primerih hitrost čistega Python-a primerljiva s knjižnico numpy. Prednost knjižnice numpy se pokaže v primerih, ko imamo opravka z velikimi seznami, ki vsebujejo nekaj tisoč in več elementov. |
4.6.2. funkcija np.vectorize()
Praktično vse matematične operacije, ki so navedene v tej knjigi, so avtomatsko vektorizirane in dodatno delo s strani uporabnika ni potrebno.
Včasih pa se soočimo s situacijo, ko so potrebni dodatni koraki, da se lahko izvrednotijo vrednosti za vsak element posebej.
Poglejmo si primer, ko bi radi pozitivnim številom v seznamu:
seznam = np.array([-5, -3, -1, 1, 3, 5])
določili kvadratni koren, za vsa ostala števila pa bi radi vrnili vrednost -1, saj korenjenje ni mogoče (če ne vključimo kompleksnih števil).
Za ta primer lahko definiramo funkcijo:
def kvadratni_koren(x):
if x < 0:
return -1
else:
return np.sqrt(x)
Če bi radi določili vrednosti gornje funkcije za vsak element posebej, imamo dve možnosti.
Možnost brez uporabe vektorizacije je, da uporabimo zanko for:
rezultat = []
for element in seznam:
rezultat.append(kvadratni_koren(element))
print(rezultat) # izpis: [-1, -1, -1, 1.0488088481701516, 1.7888543819998317, 3.0]
Druga, v večini primerov hitrejša, možnost pa je uporaba funkcije np.vectorize():
kvadratni_koren_vektoriziran = np.vectorize(kvadratni_koren, otypes=[float]) rezultat = kvadratni_koren_vektoriziran(seznam) print(rezultat) # izpis: [-1. -1. -1. 1.04880885 1.78885438 3.]
s pomočjo katere smo definirali novo funkcijo kvadratni_koren_vektoriziran, ki je vektoriziranega tipa in omogoča izvednotenje za vsak element posebej.
|
Pri zgornji uporabi funkcije |
|
Zgornji problem bi lahko izračunali tudi brez uporabe rezultat_2 = seznam.copy() rezultat_2[seznam < 0] = -1 rezultat_2[seznam >= 0] = np.sqrt(seznam[seznam>=0]) print(rezultat_2) # izpis: [-1. -1. -1. 1.04880885 1.78885438 3.] kjer smo si pomagali z logičnim indeksiranjem predstavljenim v razdelku Logično indeksiranje. |
4.6.3. Naloge
Spodaj so navedene naloge, s katerimi utrjujemo funkcionalnosti predstavljene v razdelku Vektorizacija. Rešitve nalog najdete v razdelku Rešitve.
-
Določi seznam točk
X, ki med vrednostima -10 in 10 vsebuje 30 ekvidistantnih točk. -
Definiraj funkcijo
f_x(x), ki za negativni \(x\) vrne vrednost \(-x\), za pozitivni \(x\) pa \(x^2\). -
Vektoriziraj funkcijo
f_xin jo shrani kotf_X. -
Izvrednoti
f_X(X)in rezultat shrani v seznamY_1. -
Za vse vrednosti v seznamu
Xbrez vektorizacije izvedi enako matematično operacijo, kot jo naredif_x(x)in rezultat shrani vY_2. -
Nariši grafa obeh rešitev.
4.6.4. Rešitve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import matplotlib.pyplot as plt
# seznam x-ov
X = np.linspace(-10,10,30)
# definicija funkcije
def f_x(x):
if x < 0:
return -x
else:
return x ** 2
# vektorizacija funkcije
f_X = np.vectorize(f_x, otypes=[float])
Y_1 = f_X(X)
print("Y_1\n", Y_1)
# izračun z logičnimi indeksi
Y_2 = X ** 2
Y_2[X<0] = -X[X<0]
print("Y_2\n", Y_2)
# risanje grafov s knjižnico matplotlib
fig, axs = plt.subplots(2, 1, sharex=True)
axs[0].plot(X, Y_1)
axs[0].set_ylabel('Y_1', fontsize=12)
axs[1].plot(X, Y_2)
axs[1].set_ylabel('Y_2', fontsize=12)
axs[1].set_xlabel('Koordinata x', fontsize=12)
plt.show()
Y_1 [ 10. 9.31034483 8.62068966 7.93103448 7.24137931 6.55172414 5.86206897 5.17241379 4.48275862 3.79310345 3.10344828 2.4137931 1.72413793 1.03448276 0.34482759 0.11890606 1.07015458 2.97265161 5.82639715 9.6313912 14.38763377 20.09512485 26.75386445 34.36385256 42.92508918 52.43757432 62.90130797 74.31629013 86.68252081 100. ] Y_2 [ 10. 9.31034483 8.62068966 7.93103448 7.24137931 6.55172414 5.86206897 5.17241379 4.48275862 3.79310345 3.10344828 2.4137931 1.72413793 1.03448276 0.34482759 0.11890606 1.07015458 2.97265161 5.82639715 9.6313912 14.38763377 20.09512485 26.75386445 34.36385256 42.92508918 52.43757432 62.90130797 74.31629013 86.68252081 100. ]
Poglavje 5. Inženirski primeri
5.1. Naloga nosilec
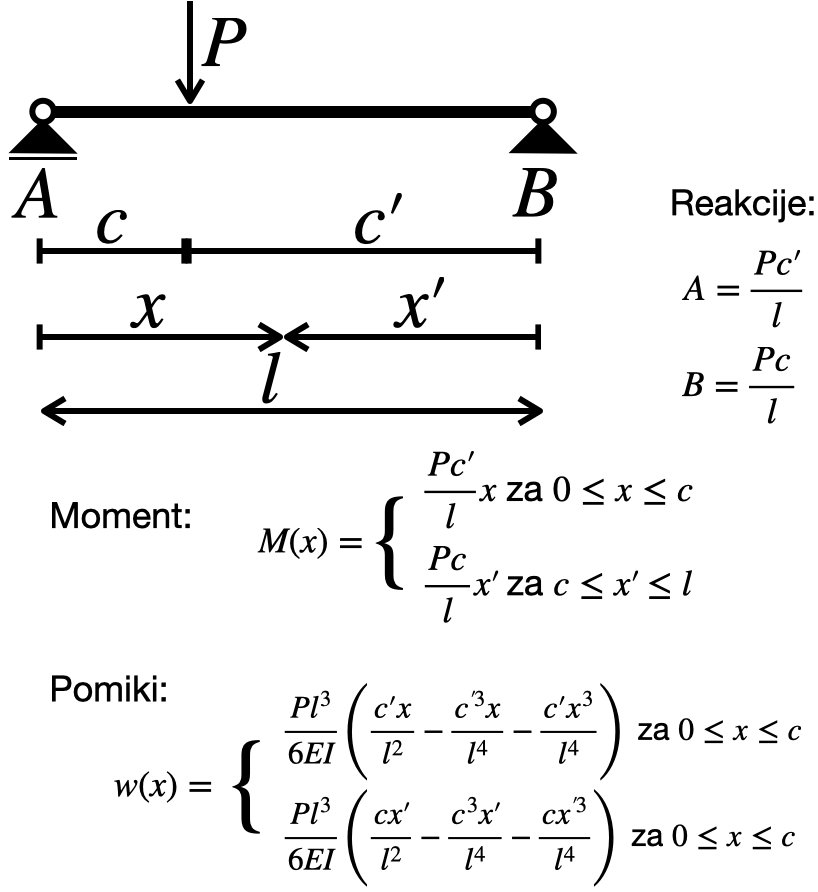
S pomočjo knjižnice numpy je potrebno v skladu s spodnjimi navodili pripraviti kodo, ki izračuna notranje količine za nosilec na sliki Prostoležeč nosilec s silo. Rešitev najdete v razdelku Rešitev.
-
Definiraj spremenljivke, v katere se shranijo podatki o nosilcu (dolžina nosilca, elastični modul, vztrajnostni moment, pozicija obtežbe, velikost obtežbe in število notranjih točk za izvrednotenje notranjih količin) in jih izpiši.
-
Določi seznam
Xv katerega shraniš pozicije notranjih točk vzdolž nosilca za izračun notranjih količin. -
Izračunaj reakciji
AinB. -
Definiraj funkcijo za izračun upogibnega momenta
m_x(x). -
Definiraj funkcijo za izračun vertikalnega pomika
w_x(x). -
Vektoriziraj funkcijo
m_x(x)in jo shrani vM_x. -
Vektoriziraj funkcijo
w_x(x)in jo shrani vW_x. -
Izvrednoti momente vzdolž nosilca in vrednosti shrani v spremenljivko
momenti. -
Izvrednoti vertikalne pomike vzdolž nosilca in vrednosti shrani v spremenljivko
pomiki. -
Za vsako točko vzdolž nosilca izpiši pozicijo, vrednost momenta in vrednost pomika.
-
Določi največje in najmanjše vrednosti upogibnega momenta in vertikalnega pomika.
-
nariši graf upogibnega momenta vzdolž nosilca, kjer upoštevaš, da so pozitivni momenti rišejo na natezno stran nosilca.
-
Nariši graf prečnega pomika vzdolž nosilca, kjer upoštevaš, da so pozitivni pomiki v smeri navzdol in jih tako tudi nariši.
5.1.1. Rešitev
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
import numpy as np
import matplotlib.pyplot as plt
print("PODATKI O NOSILCU")
# dolžina nosilca
l = 10.
print("Dolžina nosilca:", l)
# elastični modul
E = 3000.
print("Elastični modul:", E)
# Vztrajnostni moment
I = 1000.
print("Vztrajnostni moment:", I)
# pozicija obtežbe
c = 3.
c_ = l - c
print("Pozicija obtežbe:", c)
# velikost obtežbe
P = 13.
print("Obtežba P:", P)
print("\nPODATKI ZA IZRAČUN NOSILCU")
# izbrano število točk za izračun notranih sil in pomikov
st_tock = 31
print("Število točka za ozračun:", st_tock)
# pozicije točk za izračun
X = np.linspace(0,l,st_tock)
print("Pozicije točk vzdolž nosilca:\n", X)
print("\nREZULTATI")
# izračun reakcij
A = P * c_ / l
print("Reakcija A:", A)
B = P * c / l
print("Reakcija B:", B, "\n")
# funkcija za izračun upogibnega momenta v odvisnosti od x
def m_x(x):
if x < c:
return P * c_ * x / l
else:
x_ = l - x
return P * c * x_ / l
# funkcija za izračun vertikalnega pomika v odvisnosti od x
def w_x(x):
if x < c:
return P * l**3 / 6 / E / I * (c_ * x / l**2 - c_**3 * x / l**4 - c_ * x**3 / l**4)
else:
x_ = l - x
return P * l**3 / 6 / E / I * (c * x_ / l**2 - c**3 * x_ / l**4 - c * x_**3 / l**4)
# vektorizacija funkcije m_x, da lahko izračunamo za celoten seznam pozicij
M_x = np.vectorize(m_x)
# vektorizacija funkcije w_x, da lahko izračunamo za celoten seznam pozicij
W_x = np.vectorize(w_x)
# izračun momentov
momenti = M_x(X)
# izračun pomikov
pomiki = W_x(X)
print("Pozicija | Upogibni | Pomik")
for c1, c2, c3 in zip(X, momenti, pomiki):
print("%2f | %2f | %s" % (c1, c2, c3))
# izračun maksimalnih in minimalnih vrednosti
min_m = np.min(momenti)
print("Najmanjši moment:", min_m)
max_m = np.max(momenti)
print("Največji moment:", max_m)
min_w = np.min(pomiki)
print("Najmanjši pomik:", min_w)
max_w = np.max(pomiki)
print("Največji pomik:", max_w)
# risanje grafov s knjižnico matplotlib
fig, axs = plt.subplots(2, 1, sharex=True)
# graf pomikov
axs[0].plot(X, pomiki)
axs[0].set_ylabel('Pomik w', fontsize=12)
axs[0].invert_yaxis()
# graf momentov
axs[1].plot(X, momenti, label="Upogibni momenti (M)")
axs[1].set_ylabel('Moment M', fontsize=12)
axs[1].set_xlabel('Koordinata x', fontsize=12)
axs[1].invert_yaxis()
plt.show()
| vrstica | komentar |
|---|---|
1 |
Uvozimo |
2 |
Uvozimo |
4-24 |
Določimo podatke o nosilcu, vrednosti shranimo v spremenljivke |
26-29 |
Definiramo spremenljivko |
31-33 |
S funkcijo |
37-41 |
Izračunamo reakciji v levi podpori (vrednost |
43-49 |
Definiramo funkcijo |
51-57 |
Definiramo funkcijo |
60 |
Vektoriziramo funkcijo |
63 |
Vektoriziramo funkcijo |
67 |
Izvrednotimo vrednosti momentov vzdolž nosilca in jih shranimo v seznam |
70 |
Izvrednotimo vrednosti pomikov vzdolž nosilca in jih shranimo v seznam |
72-74 |
Za vse točke znotraj elementa izpišemo vrednost pozicije (koordinate), vrednost momenta in vrednost pomikov. |
76-84 |
Določimo največje in najmanjše vrednosti upogibnih momentov in vertikalnih pomikov. Vrednosti s funkcijo |
88 |
Pripravimo spremenljivke za risanje grafov, in sicer pripravimo mrežo slik, ki ima 2 vrstici in 1 stolpec. |
90-93 |
Pripravimo graf pomikov, določimo tekst na y osi ter obrnemo y os. |
95-99 |
Pripravimo graf momentov, določimo tekst na y osi ter obrnemo y os. |
101 |
Grafe prikažemo. |
PODATKI O NOSILCU Dolžina nosilca: 10.0 Elastični modul: 3000.0 Vztrajnostni moment: 1000.0 Pozicija obtežbe: 3.0 Obtežba P: 13.0 PODATKI ZA IZRAČUN NOSILCU Število točka za ozračun: 31 Pozicije točk vzdolž nosilca: [ 0. 0.33333333 0.66666667 1. 1.33333333 1.66666667 2. 2.33333333 2.66666667 3. 3.33333333 3.66666667 4. 4.33333333 4.66666667 5. 5.33333333 5.66666667 6. 6.33333333 6.66666667 7. 7.33333333 7.66666667 8. 8.33333333 8.66666667 9. 9.33333333 9.66666667 10. ] REZULTATI Reakcija A: 9.1 Reakcija B: 3.9 Pozicija | Upogibni | Pomik 0.000000 | 0.000000 | 0.0 0.333333 | 3.033333 | 8.575720164609052e-06 0.666667 | 6.066667 | 1.7039094650205758e-05 1.000000 | 9.100000 | 2.5277777777777783e-05 1.333333 | 12.133333 | 3.317942386831275e-05 1.666667 | 15.166667 | 4.0631687242798346e-05 2.000000 | 18.200000 | 4.7522222222222235e-05 2.333333 | 21.233333 | 5.373868312757201e-05 2.666667 | 24.266667 | 5.916872427983537e-05 3.000000 | 27.300000 | 6.369999999999999e-05 3.333333 | 26.000000 | 6.724691358024691e-05 3.666667 | 24.700000 | 6.983086419753084e-05 4.000000 | 23.400000 | 7.15e-05 4.333333 | 22.100000 | 7.230246913580247e-05 4.666667 | 20.800000 | 7.228641975308641e-05 5.000000 | 19.500000 | 7.149999999999998e-05 5.333333 | 18.200000 | 6.999135802469136e-05 5.666667 | 16.900000 | 6.780864197530863e-05 6.000000 | 15.600000 | 6.5e-05 6.333333 | 14.300000 | 6.161358024691357e-05 6.666667 | 13.000000 | 5.7697530864197545e-05 7.000000 | 11.700000 | 5.33e-05 7.333333 | 10.400000 | 4.846913580246913e-05 7.666667 | 9.100000 | 4.3253086419753095e-05 8.000000 | 7.800000 | 3.7699999999999995e-05 8.333333 | 6.500000 | 3.185802469135805e-05 8.666667 | 5.200000 | 2.5775308641975316e-05 9.000000 | 3.900000 | 1.9499999999999996e-05 9.333333 | 2.600000 | 1.308024691358027e-05 9.666667 | 1.300000 | 6.564197530864209e-06 10.000000 | 0.000000 | 0.0 Najmanjši moment: 0.0 Največji moment: 27.3 Najmanjši pomik: 0.0 Največji pomik: 7.230246913580247e-05
5.2. Naloga paličje
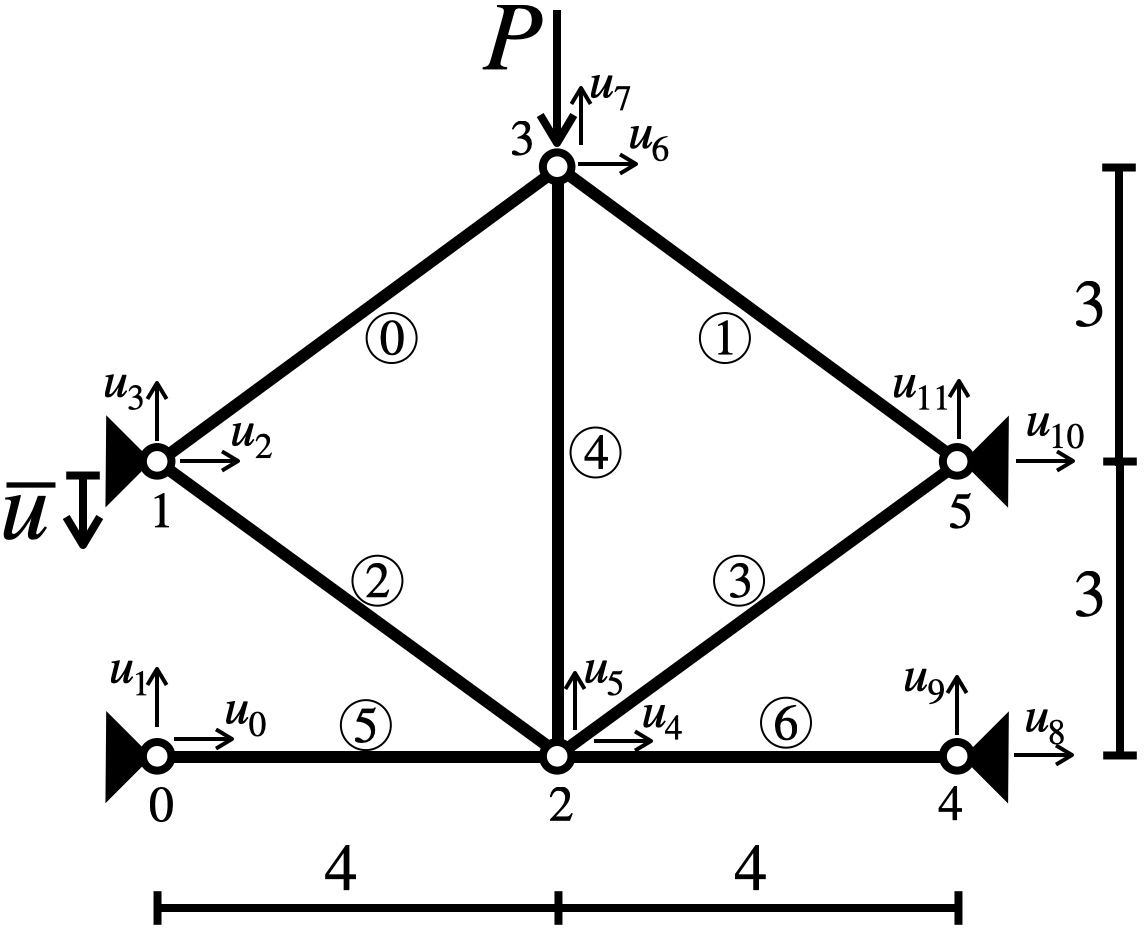
S pomočjo knjižnice numpy je potrebno v skladu s spodnjimi navodili pripraviti programsko kodo, ki izračuna pomike vozlišč za paličje na sliki Ravninsko paličje. Rešitev najdete v razdelku Rešitev.
-
Pripravi seznam koordinat vozlišč ([x0, y0], [x1, y1], … [x5, y5]) in ga shrani v spremenljivko
vozlisca. -
Izpiši indekse in koordinate vozlišč.
-
Pripravi seznam elementov ([indeks 1. vozlišča, indeks 2. vozlišča], …) in ga shrani v spremenljivko
povezave. -
Pripravi sezname:
Xi- x koordinat 1. vozlišča elementa,Yi- y koordinat 1. vozlišča elementa,Xj- x koordinat 2. vozlišča elementa,Yj- y koordinat 2. vozlišča elementa. -
Pripravi seznam dolžin elementov
Sij. -
Pripravi seznam kosinusov elementov
LinM. -
Za vse elemente izpiši indeks elementa, indeksa obeh vozlišč, dolžino elementa ter kosinuse elementa.
-
Pripravi seznam
EAi, kamor shraniš zmnožek elastičnega modula in ploščine prečnega preza. -
Pripravi seznam
Ki, kamor shraniš togostne matrike elementa zapisane v globalnem koordinatnem sistemu. -
Za vse elemente izpiši togostne matrike zapisane v globalnem koordinatnem sistemu.
-
Sestavi globalno matriko konstrukcije
K. -
Določi pomike vozlišč za primer 1, ko v vozlišču 3 deluje sila z vrednostjo 10 navzdol.
-
Določi pomike vozlišč za primer 2, ko se vozlišče 1 premakne za 3cm navzdol.
-
Manjkajoče izraze za zgornje količine lahko najdete na tej povezavi Statika linijskih konstrukcij, Zgledi za račun linijskih konstrukcij po metodi končnih elementov, 1.1 Ravninsko paličje, Janez Duhovnik, Fakulteta za gradbeništvo in geodezijo Univerze v Ljubljani, 1998.
|
Naloga je povzeta iz Statika linijskih konstrukcij, Zgledi za račun linijskih konstrukcij po metodi končnih elementov, 1.1 Ravninsko paličje, Janez Duhovnik, Fakulteta za gradbeništvo in geodezijo Univerze v Ljubljani, 1998, kjer je navedena tudi podrobna rešitev brez uporabe računalnika. |
5.2.1. Rešitev
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
import numpy as np
# primer 1.1 povzet iz https://www.klancek.si/sites/default/files/datoteke/files/mke-duhovnik.pdf
# koordinate vozlišč
vozlisca = np.array([[0,0],[0,3],[4,0],[4,6],[8,0],[8,3]])
print("Vozlišče | koordinata")
for i, v in enumerate(vozlisca):
print(f" {i} | {v}")
# Seznam povezav za vse elemente [zacetno_vozlisce, koncno_vozlisce]
povezave = np.array([[1, 3], [3, 5], [1, 2], [2, 5], [2, 3], [0, 2], [2, 4]])
# koordinate vozlišč za vse elemente
XYij = vozlisca[povezave]
# X koordinate 1. vozlišča
Xi = XYij[:,0,0]
# Y koordinate 1. vozlišča
Yi = XYij[:,0,1]
# X koordinate 2. vozlišča
Xj = XYij[:,1,0]
# Y koordinate 2. vozlišča
Yj = XYij[:,1,1]
# dolžine elementov
Sij = np.sqrt((Xj-Xi)**2+(Yj-Yi)**2)
# kosinusi elementov
L = (Xj - Xi) / Sij
M = (Yj - Yi) / Sij
# izpis podatkov o elementih
print("Elem. | i-j | sij | l | m")
for i, (v, sij, l, m) in enumerate(zip(povezave, Sij, L, M)):
print(f" {i} | {v[0]}-{v[1]} | {sij} | {l} | {m}")
# seznam EA za vse elemente, upošteva, da so vse togosti enake Ei * Ai / si = a
EAi = Sij
# Togostne matrike elementov v glavnem KS
Ki = np.zeros((len(L), 4, 4))
Ki[:,0,0] = EAi / Sij * L**2
Ki[:,0,1] = EAi / Sij * L*M
Ki[:,0,2] = EAi / Sij * -L**2
Ki[:,0,3] = EAi / Sij * -L*M
Ki[:,1,0] = EAi / Sij * L*M
Ki[:,1,1] = EAi / Sij * M**2
Ki[:,1,2] = EAi / Sij * -L*M
Ki[:,1,3] = EAi / Sij * -M**2
Ki[:,2,0] = EAi / Sij * -L**2
Ki[:,2,1] = EAi / Sij * -L*M
Ki[:,2,2] = EAi / Sij * L**2
Ki[:,2,3] = EAi / Sij * L*M
Ki[:,3,0] = EAi / Sij * -L*M
Ki[:,3,1] = EAi / Sij * -M**2
Ki[:,3,2] = EAi / Sij * L*M
Ki[:,3,3] = EAi / Sij * M**2
for el, ki in enumerate(Ki):
print("Togostna matrika elementa", el)
print(ki)
# Togostna matrika konstrukcije
K = np.zeros((len(vozlisca)*2,len(vozlisca)*2))
# Sestavljanje togostne matrike iz prispevkov posameznih elementov
for voz, ki in zip(povezave, Ki):
# indeksi vozlišč elementa
i, j = voz
# vsako vozlišč ima po 2 prostostni stopnji
# dodajanje podmatrik elemnta po delih v matriko konstrukcije
K[2*i:2*i+2,2*i:2*i+2] += ki[0:2,0:2]
K[2*j:2*j+2,2*j:2*j+2] += ki[2:4,2:4]
K[2*i:2*i+2,2*j:2*j+2] += ki[0:2,2:4]
K[2*j:2*j+2,2*i:2*i+2] += ki[2:4,0:2]
print("Globalna togostna matrika\n",K)
###################
# Primer 1, sila
###################
# Vektor obtežbe na konstrukcij za primer 1, sila 10 navzdol v vozlišču 3
F1 = np.zeros((len(vozlisca)*2))
F1[3*2+1] = -10
# Reducirana togostna matrika, samo prosti pomiki 4, 5, 6, 7
Kmm1 = K[4:8,4:8]
print("Reducirana togostna matrika primer 1:\n", Kmm1)
# Reduciran obtežni vektor
Fm1 = F1[4:8]
print("Reduciran obtežni vektor primer 1:\n", Fm1)
# Izračun neznanih pomikov za 1. primer
x1 = np.linalg.solve(Kmm1, Fm1)
print("Pomiki v prostih vozliščih primer 1:\n", x1)
###################
# Primer 2, pomik
###################
# predpisan pomik 3 za 3 cm navzdol
u2 = np.zeros((len(vozlisca)*2))
u2[3] = -0.03
# novi položaji vrstic/stolpcev, da so togosti povezane z neznanimi pomiki spodaj desno.
# 4 -> 8, 5 -> 9, 6->10, 7->11
nov_polozaj = np.array([0, 1, 2, 3, 8, 9, 10, 11, 4, 5, 6, 7])
# preurejena togostna matrika, najprej zamenjamo vrstice, nato še stolpce
K2 = K[nov_polozaj]
K2 = K2 [:, nov_polozaj]
# Reducirana togostna matrika, neznani pomiki na zadnjih 4 mestih
Kmm2 = K2[8:,8:]
print("Reducirana togostna matrika primer 2:\n", Kmm2)
# Izračun obtežnega vektorja zaradi vsiljenih pomikov
Kmr2 = K2[8:,:8]
ur2 = u2[nov_polozaj][:8]
F2 = -np.dot(Kmr2,ur2)
print("Reduciran obtežni vektor primer 2:\n", F2)
# Izračun neznanih pomikov za 2. primer
x2 = np.linalg.solve(Kmm2, F2)
print("Pomiki v prostih vozliščih primer 2:\n", x2)
| vrstica | komentar |
|---|---|
1 |
Uvozimo |
6-10 |
V spremenljivko |
13 |
Definiramo seznam elementov oziroma povezav med vozlišči in shranimo v spremenljivko |
15-24 |
Določimo koordinate prvega in drugega vozlišča za vsak element posebej in shranimo v seznam |
27 |
Določimo dolžine vseh elementov in jih shranimo v seznam |
29-31 |
Določimo kosinuse elementov in jih shranimo v seznama |
33-36 |
Za vse elemente s funkcijo |
38 |
Definiramo seznam |
41-61 |
Določimo togostne matrike za vse elemente in jih shranimo v seznam |
63-65 |
Izpišemo vrednosti togostnih matrik vseh elementov. |
68 |
Definiramo seznam |
70-82 |
Z zanko po vseh elementih sestavljamo togostno matriko konstrukcije. Dodajanje matrike posameznega elementa je razdeljeno na 4 podmatrike. Matriko |
87-89 |
Pripravimo seznam |
91-93 |
Pripravimo in izpišemo reducirano togostno matriko |
95-97 |
Pripravimo in izpišemo reduciran obtežni vektor |
99-101 |
Neznane vrednosti pomikov izračunamo, shranimo v seznam |
108-110 |
Pripravimo seznam |
114 |
Določimo nove položaje vrstic oziroma stolpcev z namenom, da so togosti povezane z neznanimi pomiki spodaj in desno v togostni matriki. |
116-118 |
Preuredimo togostno matriko in jo shranimo v spremenljivko |
120-122 |
Pripravimo in izpišemo reducirano togostno matriko |
124-128 |
Pripravimo in izpišemo reduciran obtežni vektor |
130-132 |
Neznane vrednosti pomikov izračunamo, shranimo v seznam |
Vozlišče | koordinata 0 | [0 0] 1 | [0 3] 2 | [4 0] 3 | [4 6] 4 | [8 0] 5 | [8 3] Elem. | i-j | sij | l | m 0 | 1-3 | 5.0 | 0.8 | 0.6 1 | 3-5 | 5.0 | 0.8 | -0.6 2 | 1-2 | 5.0 | 0.8 | -0.6 3 | 2-5 | 5.0 | 0.8 | 0.6 4 | 2-3 | 6.0 | 0.0 | 1.0 5 | 0-2 | 4.0 | 1.0 | 0.0 6 | 2-4 | 4.0 | 1.0 | 0.0 Togostna matrika elementa 0 [[ 0.64 0.48 -0.64 -0.48] [ 0.48 0.36 -0.48 -0.36] [-0.64 -0.48 0.64 0.48] [-0.48 -0.36 0.48 0.36]] Togostna matrika elementa 1 [[ 0.64 -0.48 -0.64 0.48] [-0.48 0.36 0.48 -0.36] [-0.64 0.48 0.64 -0.48] [ 0.48 -0.36 -0.48 0.36]] Togostna matrika elementa 2 [[ 0.64 -0.48 -0.64 0.48] [-0.48 0.36 0.48 -0.36] [-0.64 0.48 0.64 -0.48] [ 0.48 -0.36 -0.48 0.36]] Togostna matrika elementa 3 [[ 0.64 0.48 -0.64 -0.48] [ 0.48 0.36 -0.48 -0.36] [-0.64 -0.48 0.64 0.48] [-0.48 -0.36 0.48 0.36]] Togostna matrika elementa 4 [[ 0. 0. -0. -0.] [ 0. 1. -0. -1.] [-0. -0. 0. 0.] [-0. -1. 0. 1.]] Togostna matrika elementa 5 [[ 1. 0. -1. -0.] [ 0. 0. -0. -0.] [-1. -0. 1. 0.] [-0. -0. 0. 0.]] Togostna matrika elementa 6 [[ 1. 0. -1. -0.] [ 0. 0. -0. -0.] [-1. -0. 1. 0.] [-0. -0. 0. 0.]] Globalna togostna matrika [[ 1. 0. 0. 0. -1. 0. 0. 0. 0. 0. 0. 0. ] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [ 0. 0. 1.28 0. -0.64 0.48 -0.64 -0.48 0. 0. 0. 0. ] [ 0. 0. 0. 0.72 0.48 -0.36 -0.48 -0.36 0. 0. 0. 0. ] [-1. 0. -0.64 0.48 3.28 0. 0. 0. -1. 0. -0.64 -0.48] [ 0. 0. 0.48 -0.36 0. 1.72 0. -1. 0. 0. -0.48 -0.36] [ 0. 0. -0.64 -0.48 0. 0. 1.28 0. 0. 0. -0.64 0.48] [ 0. 0. -0.48 -0.36 0. -1. 0. 1.72 0. 0. 0.48 -0.36] [ 0. 0. 0. 0. -1. 0. 0. 0. 1. 0. 0. 0. ] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [ 0. 0. 0. 0. -0.64 -0.48 -0.64 0.48 0. 0. 1.28 0. ] [ 0. 0. 0. 0. -0.48 -0.36 0.48 -0.36 0. 0. 0. 0.72]] Reducirana togostna matrika primer 1: [[ 3.28 0. 0. 0. ] [ 0. 1.72 0. -1. ] [ 0. 0. 1.28 0. ] [ 0. -1. 0. 1.72]] Reduciran obtežni vektor primer 1: [ 0. 0. 0. -10.] Pomiki v prostih vozliščih primer 1: [ 0. -5.10620915 0. -8.78267974] Reducirana togostna matrika primer 2: [[ 3.28 0. 0. 0. ] [ 0. 1.72 0. -1. ] [ 0. 0. 1.28 0. ] [ 0. -1. 0. 1.72]] Reduciran obtežni vektor primer 2: [ 0.0144 -0.0108 -0.0144 -0.0108] Pomiki v prostih vozliščih primer 2: [ 0.00439024 -0.015 -0.01125 -0.015 ]
Poglavje 6. Dodatni viri
Pri pripravi dokumenta so bile v pomoč naslednje spletne strani in pripadajoče vaje (angl. tutorial):