ESDEP WG 17
SEISMIC DESIGN
To give an overview of the methods used for the analysis of structures under seismic actions.
Basic knowledge of structural analysis and structural dynamics
Lecture 17.2: Introduction to Seismic Design - Seismic Hazard and Seismic Risk
Lecture 17.3: The Cyclic Behaviour of Steel Elements and Connections
The lecture briefly presents the methods stipulated by modern design codes for the analysis of structures under seismic actions. Time-domain methods are briefly described and the scope of their application is specified. Emphasis is given to the response spectrum method as the standard procedure proposed by, for example, Eurocode 8 [1]. In addition, a simplified response spectrum method for regular buildings is presented. Finally inelastic behaviour and its role in design under seismic actions is discussed.
Several methods are available for the structural analysis of buildings and other civil engineering works under seismic actions. The differences between the methods lie (a) in the way they incorporate the seismic input and (b) in the idealization of the structure. All methods of analysis must serve the current design philosophy for seismic actions which requires that a structure must not collapse and must retain its structural integrity under the so-called "strong" earthquake. The structure also must be protected against damage and limitations of use under the so-called "moderate" earthquake. To avoid collapse, the structure is allowed to develop plastic zones in which seismic energy is dissipated.
Details of the basic requirements of seismic behaviour of structures, and the criteria needed for ensuring compliance with these requirements, can be found in all modern seismic design codes, e.g. Eurocode 8 [1].
Due to the dynamic nature of seismic excitation, the actual displacements and stresses developed in a structure are time dependent, i.e. they are functions of time (t). To analyze a structure under dynamic loads, efficient methods have been developed that discretize and solve the model of the structure on the basis of the Finite Element Method. Within this framework there exist methods that can perform a linear or non-linear analysis, i.e. elastic, small deformation, or inelastic, large deformation analysis for a given seismic excitation, expressed in the form of an accelerogram a(t). The cost of such analysis is generally high, while the results correspond to a particular excitation and, as such do not offer a reliable basis for design. To increase the reliability of the method, a set of artificial accelerograms that represent the seismicity of a particular region is usually generated. This procedure, however, renders the method very expensive.
Eurocode 8 [1] considers the use of time domain dynamic analysis, i.e. a direct dynamic analysis performed by numerical integration of the differential equations of motion. It stipulates conditions for the use of artificially generated accelerograms and discusses the overall reliability of the method. The reliability must be at least the same as that obtained by the standard procedure of the Code which is the response spectrum method. Although the direct dynamic methods can perform a close-to-reality analysis, this approach is justified and can be employed effectively only for large and complex structures. It is used where no previous experience of the structural behaviour exists, or for detailed evaluation of the response of existing structures under specific earthquakes.
The cost of an analysis based on the finite element method can be kept reasonable by using only line elements and by avoiding the use of surface elements. The mass of the structure of buildings is mainly concentrated at the floor levels. This distribution permits the treatment of all the masses of the structure as lumped at the floor levels in dynamic analysis. The dynamic degrees of freedom for which inertia forces are developed can then be reduced to a reasonable number. All the remaining kinematical degrees of freedom control the statics of the structure, and can then be expressed in terms of the dynamic degrees of freedom. In this way the number of differential equations that express the dynamic response of the system can be reduced to a small number, leading to reasonable and acceptable solutions.
The time dependent solutions discussed above express the dynamic response of the structure due to a particular earthquake given in the form of an accelerogram. They do not offer the required information for design however, because one particular earthquake cannot be representative of the seismicity of the area under consideration.
In order to define an envelope of different earthquakes and also to eliminate the factor of time, the concept of the response spectrum was developed. The response spectrum provides the required information for design purposes and, at the same time, simplifies the analysis by reducing the problem to a static problem of the estimated maximum responses. The response spectrum is defined, on a single degree of freedom system of varying frequency excited by a specific earthquake, as the maximum response of the system, ignoring the particular time of its occurrence. If the response is the displacement of the system then the displacement spectrum is formed. If the response is the velocity or the acceleration, the velocity or acceleration spectra are developed. The acceleration response spectrum is of primary interest in earthquake engineering. More details about earthquake response spectra are given in Lecture 17.2.
The response spectrum method of analysis is the standard design procedure of modern seismic design codes, e.g. Eurocode 8. It aims to give directly the maximum effects of the earthquake in the various elements of the structure.
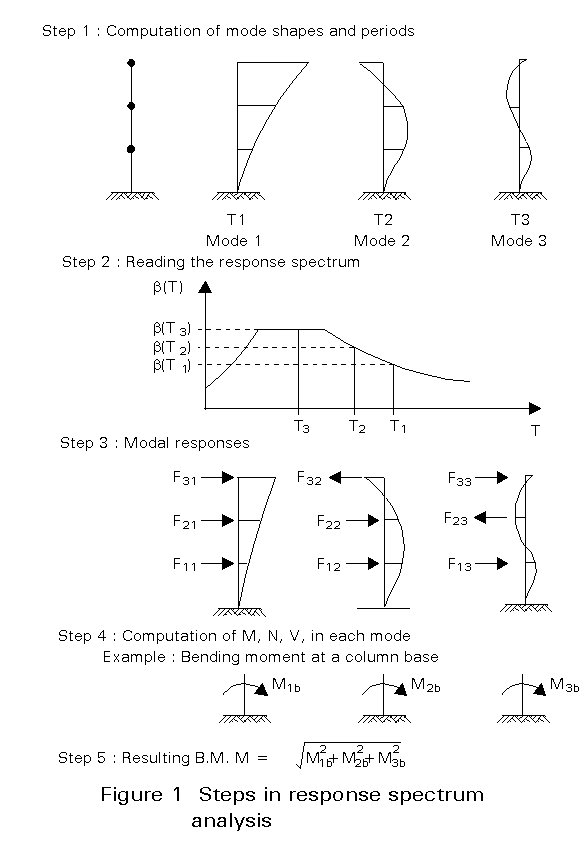
The general method, called also the multi-modal method, consists of computing the various modes of vibration of the structure and the magnitude of the maximum response in each mode with reference to a response spectrum. A rule is then used to combine the responses of the different modes. For this reason the method is also known as the superposition of modal responses method, although the same name is used for linear dynamic analysis where the mode shapes are used to decouple the differential equations of motion and convert the n-degree of freedom coupled system to n-single degree of freedom systems. The combination rule will generally be a square root of the sum of squares (SRSS) of the various modal responses. This combination rule must be applied to all computed quantities, i.e. bending moments, shear forces, normal forces and displacements. As a consequence, the resulting internal forces do not represent an equilibrated set. Where the frequencies of a structure do not differ by more than 10%, different combination rules need to be employed. In Figure 1 the steps of such an analysis by means of the response spectrum are briefly summarised.

The response spectrum method is valid only for linear behaviour of a structure, i.e. only for an elastic analysis with small deformations. For this reason the term elastic response spectrum is generally used. However an equivalent method can be developed which results from comparative linear and non-linear analyses. It uses a modified response spectrum such that the output internal forces from a linear analysis will be correlated with the non-linear ones. This modified spectrum is referred to as the design response spectrum. It is derived from the elastic spectrum modified by factors that take into account the influence of the non-linearity of the structural material, the soil and other damping characteristics. In Figure 2 the design response spectra to be used in the analysis of structures, as given in Eurocode 8 [1], are shown schematically.
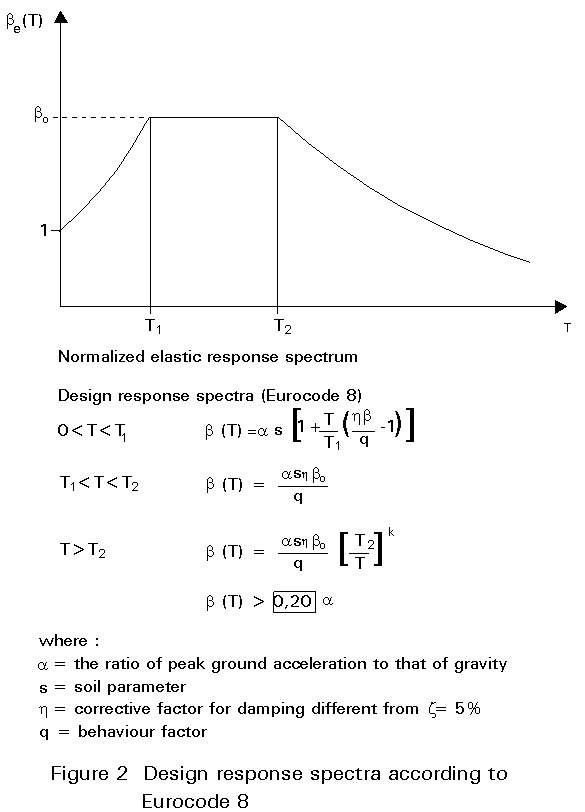
The main advantage of using the design response spectrum is that the analysis is linear while the results represent the non-linear response of the structure.
A more simplified procedure than the multi-modal method, is the so-called equivalent static force analysis, sometimes also called, e.g. in Eurocode 8 [1], the simplified dynamic analysis. This method is a particular application of the design response spectrum method where one particular mode of vibration is predominant as compared to others. This is the case for regular buildings (regular stiffness and mass distribution over the height of the building according to Eurocode rules, see Lecture 17.5). The system is accurately modelled by a single degree of freedom system. In essence the design spectrum method is reduced to one mode of vibration to express the dynamic behaviour of the system. Usually the first flexural mode shape is considered as a primary mode of vibration which can be simplified further into a simple line. The equivalent static forces are computed as shown in Figure 3. A classical static analysis can then be performed under the action of these equivalent static forces. The only prerequisite of the method is the fundamental period of vibration T of the structure. It needs to be calculated in order to find the appropriate design spectrum value b(T), necessary to compute the base shear V. Alternatively, if an accurate value of the period T is not available, the value of the fundamental period can be calculated approximately by using one of the recommended formulae.
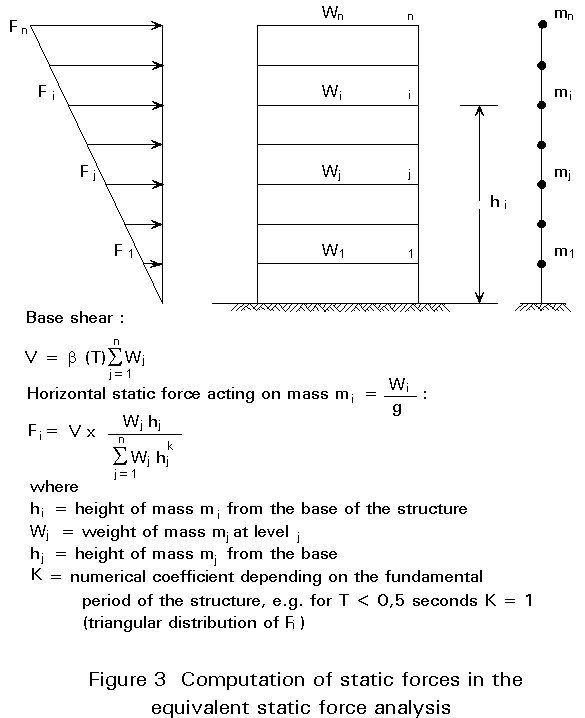
The equivalent static force method is an approximate method which is adequate for certain types of structures and for the preliminary design of other structures. There may be cases where this method is not conservative because the contribution from higher modes of vibration may be significant. For these cases a complete dynamic response spectrum analysis is advisable for the final design stage.
In Table 1 a summary of the possible methods of structural analysis under seismic actions is presented. Moreover the following remarks can be made:
It is clear from the above discussion that the design of an earthquake resistant structure is a complex task which requires engineering judgement. It must be performed by experienced engineers. The blind use of computer software as blackboxes may result in inadequate design.
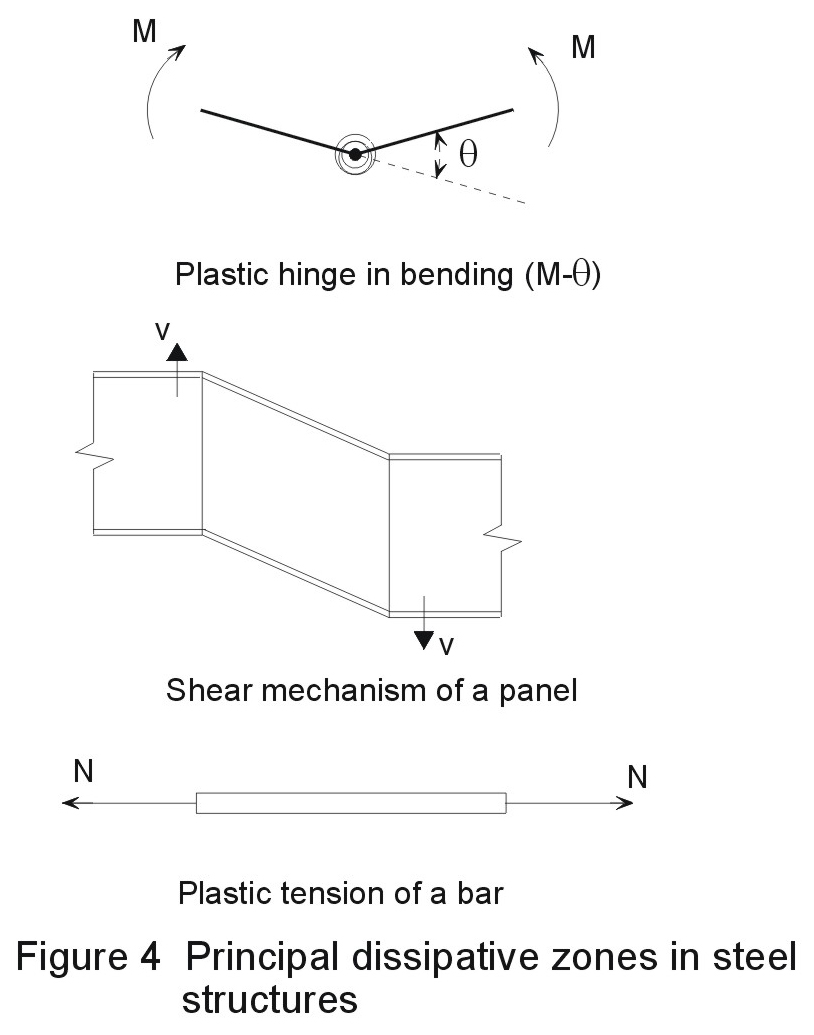
The elastic design of an earthquake resistant structure leads to very expensive structures. Moreover it is not consistent with the current design philosophy which seeks to establish controlled dissipative zones in the structure where seismic energy can be dissipated by means of ductile hysteretic behaviour. The principal dissipative zones in steel structures are plastic hinges (in bending), sheared web panels and members under plastic tension (Figure 4).
In Figure 5 the difference in energy dissipation between the elastic and inelastic concept is presented. The energy input Ei of an earthquake is counterbalanced inside the structure by the following sum of terms:
Ei = Ee + Ed + Eye + Ekin
where
Ee is the energy of elastic strain
Ed is the energy dissipated in a viscoelastic way
Eye is the energy dissipated by yielding
Ekin is the kinetic energy.

To obtain a stable earthquake resistant structure, either the energy input is minimized by means of special techniques, such as base isolation of the building, or the dissipative terms in the right hand side of the equation are increased. The term Eye must be increased as much as possible. It should be noted that by taking into account elastoplastic energy dissipation, a considerable weight reduction of the structure is achieved. In Figure 6 the moment rotation diagram of two equivalent beam elements is considered from the point of view of energy dissipation. The resisting moment M1 required to resist an earthquake elastically, is 3 times greater than the resisting moment M2 of the elastoplastic element with a ductility of 2. Expressed in terms of weight, beam 2 is only equivalent to 0,6 of beam 1. Thus the ductile behaviour allows for substantial economy in the size of the elements of a structure. This economy is even more substantial since the local ductility can be higher than 2. In steel structures the value of local ductility can be as high as 10.

In order to design structures with dissipative behaviour by employing an elastic analysis which is easy for the design office, certain rules have to be followed. They assure the safe formation of as many as possible local dissipative zones, avoiding local failure mechanisms.
To approximate the results of a non-linear dynamic analysis by performing an elastic analysis, the conventional response spectrum method is modified by reducing the spectrum in some way to account for the inelastic energy dissipation of the real structure under the earthquake action.
This reduction is accomplished by using the structural behaviour factor q. It can generally be defined as the ratio between the maximum accelerogram that a structure can withstand without failure and the accelerogram for which yielding appears somewhere in the structure. The definition is general and can be applied to different quantities of interest. In steel structures, one way to establish the correlation between a conventional elastic analysis and the real inelastic behaviour is as follows:
For a given structure under a specific earthquake action a(t), a series of computations of the non-linear dynamic response is performed by applying actions l(t), where l is a multiplier. By increasing the value of l the following successive situations emerge (Figure 7) [2, 3]:
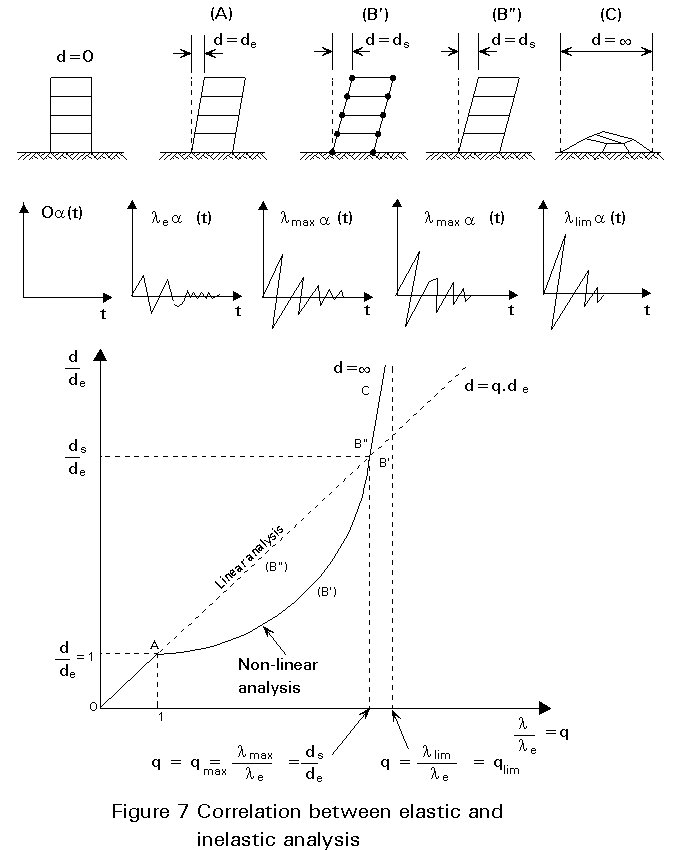
The behaviour factor q, is then defined as:
q = lmax /le
Thus the existence of a meeting point between the two forms of behaviour, allows a direct link between the linear and non-linear computations. The equivalence states that, for a given accelerogram a(t) and a known value of q, the usual linear analysis under the action a(t)/q and the usual checks on stresses, give the same safety level as the dynamic non-linear calculations under the action of a(t). This equivalent is due to the counteraction of the yielding effect which reduces the displacements, and the P-D effect on the structure which increases the displacements.
The real displacements of the structure ds are given as q times the elastic displacements de calculated by using the reduced forces, i.e.
ds = q de
The values of the factor q for various types of steel buildings are given in Lecture 17.5. All recent design codes use a similar approach with slightly different values for the q factor. These discrepancies are justified by the fact that q factors are not only functions of the shape of the structure, but they depend also on the accelerograms a(t) considered. The accelerograms differ from one part of the world to the other. Other points of difference may be due to the selected parameter characterizing the behaviour, which may be the equal energy dissipation rather than the displacements, and due to the safety factors used for the elastic analysis, which usually are higher than those used for the inelastic analysis. Thus the appropriate q factors involve a theoretical approach but also an engineering judgement.
It should be noted also that the analysis using a q reduction factor for an earthquake action is conventional. Safety in the various structural elements is assured by requiring the computed comparison stresses to be less than or equal to the yield stress. For the design of connections, under a real earthquake, the real comparison stresses are equal to fy in dissipative zones. It is for this reason that connections close to dissipative zones must be designed to transmit the plastic design resistance of elements and not the elastic internal forces computed on the basis of an elastic analysis using a q reduction factor.
[1] Eurocode 8: "Structures in Seismic Regions - Design", CEN, (in preparation).
[2] Ballio, G. (1985) ECCS Approach for the Design of Steel Structures to Resist Earthquakes. Symposium on Steel in Buildings, Luxembourg. IASE-AIPC-IVBH Report Volume 48 pp 313-380.
[3] Ballio, G. (1990) European Approach to Design of Steel Structures. 1990, Proc of Hong Kong Fourth World Congress - Tall Buildings: 2000 and Beyond, pp 935-946.
Table 1: Methods of analysis for structures under seismic actions
|
Data needed |
Type of analysis |
Use - Design Codes |
|
DIRECT DYNAMIC ANALYSIS (Time domain) × Accelerogram a(t)(real or artificial) × Characteristics of the structure, elastic & inelastic (e.g. M-q curves for connections) |
× Linear or non-linear× Direct Integration |
× procedure permitted by Codes but not for design× Use only for large and complex structures× Use for evaluation of response of existing structures under a specific earthquake |
|
RESPONSE SPECTRUM ANALYSIS × Design Response Spectrum× Characteristics of the structure, elastic only |
× Modal analysis (linear)× Mode shape superposition |
× Standard design procedure in Seismic Codes× No limitations of use |
|
EQUIVALENT STATIC FORCE ANALYSIS × Design Response Spectrum× Characteristics of the structure, elastic only |
× Static analysis× First vibration mode is predominant |
× Procedure permitted by Codes for buildings with specific limitations of regularity |