Example 2.1: discrete system
l
º PAB, BC and CD are rigid bars The system has two degrees
connected by rotational springs of freedom: q1, q2
of stiffness K1, K2
Assuming that q1 and q2 are small (sin q1 » q1, sin q2 » q2, cos q1 » 1, cosq2» 1) the equilibrium equations
![]()
![]()
lead to the following system of equations, written in matrix form
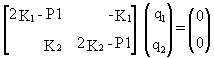
The corresponding iteration scheme is
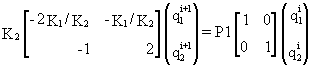
where the R.H.S. represents the internal forces (bending moments in B and C). After each iteration, by equating {q}i+1 to {q}i it is possible to obtain a lower bound, an upper bound and an estimate of Pcr. We consider now two cases:
(i) K1 = K2 = K
|
i |
{q}i |
Int.forces (x P1) |
{q}i+1 (x P1/3K) |
{q}i+1/{q}i (x P1/3K) |
L.Bound (x K/1) |
U.Bound (x K/1) |
Estimate (x K/1) |
|
1 |
|
|
|
|
0 |
1.5 |
- |
|
2 |
|
|
|
|
0.75 |
1.2 |
0.923 |
|
3 |
|
|
|
|
0.923 |
1.071 |
0.992 |
\
0.923{q}I » ![]()
Exact results: Pcr = 1 ![]() {q}I =
{q}I = ![]()
(ii) K1 = 2K2 = K
|
i |
{q}i |
Int.forces (x P1) |
{q}i+1 (x P1/3K) |
{q}i+1/{q}i (x P1/3K) |
L.Bound (x K/1) |
U.Bound (x K/1) |
Estimate (x K/1) |
|
1 |
|
|
|
|
0 |
1.5 |
- |
|
2 |
|
|
|
|
0.5 |
1 |
0.667 |
|
3 |
|
|
|
|
0.6 |
1.75 |
0.667 |
\
0.6Exact results: Pcr = 0.634 ![]() {q}I =
{q}I = ![]()
NOTE: The estimates of the critical load ![]() were obtained by averaging the values of {q}i+1/{1}i.
were obtained by averaging the values of {q}i+1/{1}i.
Example 2.2: continuous sytems
The critical buckling load of an axially loaded column with arbitrary boundary conditions is the lowest eigenvalue of the following eigenvalue-eigenfunction problem:
![]() (1)
(1)
where the axial force N is assumed to depend on a single load parameter l . Here we will be concerned only with problems in which N is piecewise constant, which means that equation (1) becomes:
![]() (2)
(2)
One observes that equation (2) is equivalent to:
![]() (3)
(3)
where the bending moment M (x, l ) has the form
M (x, l ) = N (l ) y (x) + A (l ) . x + B (l ) (4)
and the values of A (l ) and B (l ) may be determined from the boundary conditions. It should be noticed that the application of Vianello's method requires the calculation of M (x,l ) in each iteration (step (ii)) which, particularly in the case of statically indeterminate columns, may involve considerable effort. Here, only the very simple case of a simple supported column under uniform compression will be considered in order to illustrate the application of the method to a continuous system.
Since, in this case, A (l ) = B (l ) = 0, the differential equation of equilibrium is given by
![]() and leads to the iteration scheme
and leads to the iteration scheme ![]()
i = 1
Assume the initial estimate of the deflected configuration of the column as y1 (x)=![]() (L - x), noticing that it must satisfy the kinematic boundary conditions y1 (0) = y1 = 0. Then, multiplying by P to obtain the corresponding bending moment, integrating twice and imposing the boundary conditions one is led to:
(L - x), noticing that it must satisfy the kinematic boundary conditions y1 (0) = y1 = 0. Then, multiplying by P to obtain the corresponding bending moment, integrating twice and imposing the boundary conditions one is led to:
![]()
Now define
![]()
and obtain an upper bound and a lower bound of Pcr by equating [Q1(x)]max and [Q1(x)]min to the unity:
![]()
![]()
To calculate estimates of the critical load it is necessary to define criteria of similarity between y1(x) and y2(x). Two possible criteria are:
(a) To equate the average values
(y1)av = ![]()
![]()
(y2)av = ![]()
(b) To equate y1 (L/2) and y2 (L/2)
![]()
i = 2
Repeating the procredure with the initial estimate
y2(x) = x ![]()
(same shape as the result of interation 1)
one obtains
y3(x) = ![]()
Q2 (x) = ![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
(a) (y2)av = (y3)av Þ ![]() = 9.882
= 9.882 ![]()
(b) y2 (L/2) = y3 (L/2) Þ ![]() = 9.836
= 9.836 ![]()
Estimate of buckling mode: y1(x) » ![]()
Exact results: Pcr = p 2 ![]() yI(x) = sen
yI(x) = sen ![]()
Consider the beam represented in Figure 2, which is divided into 6 equal segments of length 1.
FIGURE 2
i) Distributed loads (q)
0 -1 -2 0 0 0 0 ![]()
ii) Equivalent concentrated loads (qdisc)
Linear disc. -1 -6 -5/0 0 0 0 0 ![]()
(-5)
iii) Concentrated Loads (Q)
0 0 0 0 -6 0 -3 ![]()
iv) Total concentrated loads (Fdisc)
-1 -6 -5 0 -6 0 -3 ![]()
v) Uncorrected average shears (V¢ )
The calculation starts from the right, so that the average shears are known on the basis of only one arbitrary value, which is RE = 0
20 14 9 9 3 3 ![]()
vi) Uncorrected bending moments (M¢ )
Same direction as in V¢ . Influence of RE missing. Includes a jump in pointC due to the concentrated moment.
-64 -44 -30 -21/-15 -6 -3 0 ![]()
vii) Bending moment correction (Mcorr)
The correction is due to RE and is based on the fact that MB = 0. It is linear between E and A.
50 40 30 20 10 0 0 ![]()
viii) Average shear correction (Vcorr)
It is the value of RE, i.e. the slope of Mcorr
-10 -10 -10 -10 -10 0 ![]()
ix) Average shears (V) v) + viii)
10 4 -1 -1 -7 3 ![]()
x) Bending moments (M) vi) + viii)
-14 -4 0 -1/5 4 -3 0 ![]()
xi) Curvatures (c )
-7 -2 0 -0.5/5 4 -3 0 ![]()
xii) Equivalent concentrated curvatures (c disc)
In point C, due to the jump in curvature the formula for end stations must be used twice.
Parab.disc. -61 -54 -5 -1.5/62 84 -52 -22 ![]()
(60.5)
xiii) Uncorrected average slopes (q ¢ )
The calculation starts from the left, so that the average slopes are known on the basis of only one arbitrary value, which is the discontinuity in slope in point B.
-61 -115 -120 -59.5 24.5 -27.5 ![]()
xiv) Uncorrected deflections (y¢ )
Same directions as in q ¢ . Influence of _q B missing.
0 -61 -176 -296 -355.5 -331 -358.5 ![]()
xv) Deflection correction (ycorr)
The correction is due to _q B and is based on the fact that yE = 0. It is linear between B and F.
0 0 0 110.33 220.67 331 441.33 ![]()
xvi) Average slope correction (q corr)
It is the value of _q B, i.e. the slop of ycorr
0 0 110.33 110.33 110.33 110.33 ![]()
xvii) Average slopes (q ) xiv) + xv)
-61 -115 -9.67 50.83 134.83 82.83 ![]()
xviii) Deflections (y) xiv) + xv)
0 -61 -176 -185.67 -134.83 0 82.83 ![]()
Example 4.1: Simply-supported column
i = 1
-1 -1 1 1 _y
-1 -1 1 1 P _M
-4 -24 -44 -24 -4 ![]() c disc
c disc
-4 -28 -72 -96 ![]() q ¢
q ¢
Now it is necessary to equate y1 to y0:
- 46 34 46 0 ![]() y1/y0
y1/y0
Considering the smallest and largest values of y1/y0 one obtains an upper bound and a lower bound of Pcr:
![]()
![]()
By considering the average of the values of y1/y0 one obtains and estimate of Pcr:
![]()
i = 2
-1 -0.478 0.478 1 _y
-1 -0.478 0.478 1 P _M
-4.522 -22.956 -33.56 -22.956 -4.522 ![]() c disc
c disc
-4.522 -27.478 -61.038 -83.994 -4.522 ![]() q ¢
q ¢
- 39.736 38.238 39.736 - ![]() y2/y1
y2/y1
9.664 ![]() £ pcr £ 10.042
£ pcr £ 10.042 ![]()
![]() = 9.787
= 9.787 ![]()
Exact result: Pcr = p 2 ![]() = 9.870
= 9.870 ![]()
Example 4.2
i = 1
-0.5 -0.5 -1 -2 _y
-1.5 -1.5 -1 -2 P _M
-3 2.25 1.5/3 2 0 ![]() c
c
(145.5)
- 66 120 176.25 157.75 ![]() y1/y0
y1/y0
2.179 ![]() £ Pcr £ 5.818
£ Pcr £ 5.818 ![]()
i = 2
-0.28 -0.72 -1.94 -2.32 _y
-0.84 -2.16 -1.94 -2.32 P _M
(71.71)
- 128.71 136.8 105.22 102.05 ![]() y2/y1
y2/y1
2.807 ![]() £ Pcr £ 3.763
£ Pcr £ 3.763 ![]()
![]() = 3.249
= 3.249 ![]()
Exact result: Pcr = 3.217 ![]()
Example 4.3
Since the column is statically indeterminate it is necessary to use the force method. The basis system is defined by suppressing the support at C.
0 0.5 1 0.8 0 y0 initial guess
i) Calculation of the flexibility
0 0 0 0 1 Fdisc
-1 -1 -1 -1 V
4 3 2 1 0 ![]() M
M
4 3 2 1 0 ![]() c
c
Lin.disc. 11 18 12 6 1 ![]() c disc
c disc
11 29 41 47 ![]() q
q
0 11 40 81 128 ![]() yº
yº ![]()
ii) Iteration procedure
i = 1
Basic system:
0 0.5 1 0.8 0 y0
-0.5 -0.5 0.2 0.8 _y
-1 -1 -1/0 0 0 p P
lin.disc. -3 -6 -3/0 0 0 ![]() pdisc
pdisc
(-3)
18 0 0 0 -6 ![]() P
P
15 -6 -3 0 -6 ![]() Fdisc
Fdisc
15 9 6 6 ![]() N
N
-7.5 -4.5 1.2 4.8 ![]() _M
_M
6 -1.5 -6 -4.8 0 ![]() M
M
6 -1.5 -6 -4.8 0 ![]() c
c
39 -30 -132.6 -108 -22.8 ![]() c disc
c disc
39 9 -123.6 -231.6 ![]() q
q
0 39 48 -75.6 -307.2 ![]() y
y
Calculation of Rc:
-307.2 ![]() + 128
+ 128 ![]() Rc = 0 Þ Rc = 01. p
Rc = 0 Þ Rc = 01. p
Calculation of y1:
y1 = y + 0.1 p ![]()
0 65.4 144 118.8 0 ![]() y1
y1
- 130.8 144 148.5 - ![]() y1/y0
y1/y0
62.061 ![]() £ (pl)cr £ 70.459
£ (pl)cr £ 70.459 ![]()
i = 2
Basic system:
0 0.454 1 0.825 0 y1
-0.454 -0.546 0.175 0.825 _y
15 9 9 9 ![]() N
N
-6.81 -4.914 1.05 4.95 ![]() _M
_M
5.724 -1.086 -6 -4.95 0 ![]() M
M
5.724 -1.086 -6 -4.95 0 ![]() c
c
39.55 -22.27 -132.07 -111 -23.7 ![]() c disc
c disc
39.55 17.28 -114.74 -225.74 ![]() q
q
0 39.55 56.83 -57.96 -283.75 ![]() y
y
Rc = 0.09237 p
0 63.93 145.50 121.60 0 ![]() y2
y2
- 140.81 145.50 147.39 - ![]() y2/y1
y2/y1
62.528 ![]() £ (pl)cr £ 65.81
£ (pl)cr £ 65.81 ![]()
![]() = 63.744
= 63.744 ![]()
Exact result: (pl)cr = 59.81 ![]()
One observes that the method converges to a value which is larger than the exact result. This is mainly due to the error introduced by the discretisation of p and c . In fact, solving this problem with 8 segments and an initial guess of
after 3 iterations, to 59.80 ![]() £ (pl)cr £ 60.28
£ (pl)cr £ 60.28 ![]()
Example 5.1
P = 5 ![]() = 0.507Pcr
= 0.507Pcr
q = ![]() =
= ![]()
i) Problem I
-1 -1 -1 -1 -1 ![]() q
q
-1 -2 -2 -2 -1 ![]() qdisc º Fdisc
qdisc º Fdisc
-1 -3 -5 -7 ![]() V¢
V¢
0 -1 -4 -9 -16 ![]() M¢
M¢
0 4 8 12 16 ![]() Mcorr
Mcorr
0 3 4 3 0 ![]() M
M
0 3 4 3 0 ![]() c
c
7 34 46 34 7 ![]() c disc
c disc
7 41 87 121 ![]() q ¢
q ¢
0 7 48 135 256 ![]() y¢
y¢
0 -64 -128 -192 -256 ![]() ycorr
ycorr
0 -57 -80 -57 0 ![]() y º yI
y º yI
ii) Iteration procedure
i = 1
Using the first iteration in example 4.1, which corresponds to the solution of Problem II, one obtains
0 46 68 46 0 ![]() yII
yII
Calculation of _
_ (0 + 1 + 2 + 1 + 0) = ![]() (0 + 46 + 68 + 46 + 0) +
(0 + 46 + 68 + 46 + 0) + ![]() (0 - 57 - 80 - 57 -0)
(0 - 57 - 80 - 57 -0)
\ _ = -0.00824 L
Calculation of y1 (x):
y1 (x) = yI (x) + yII (x) [_ = -0.008324 L]
0 -0.00957 -0.01381 -0.00957 0 L y1
i = 2
Problem II
0 -1 -1.443 -1 0 _ y1
0 1 1.443 1 0 ![]() M
M
0 1 1.443 1 0 ![]() c
c
2.279 11.443 16.43 11.443 2.279 ![]() c disc
c disc
2.279 13.722 30.152 41.595 ![]() q ¢
q ¢
0 2.279 16.001 46.153 87.748 ![]() _ y¢
_ y¢
0 -21.937 -43.874 -65.811 -87.748 ![]() _ ycorr
_ ycorr
0 -19.658 -27.874 -19.658 0 ![]() _ y
_ y
Calculation of _:
_ (-3.443) = ![]() (-67.14) +
(-67.14) + ![]() Þ _ = 0.00932 L
Þ _ = 0.00932 L
Calculation of y2 (x):
0 -0.00941 -0.01328 -0.00941 0 L y2
Exact result: y (L/2) = -0.01326 L
If the initial imperfection consists of an eccentricity e0 of all the applied loads, then yI (x) is the solution of (N piecewise constant):
![]() = - N e0 (x) + Ax + B (9)
= - N e0 (x) + Ax + B (9)
Finally, it should be mentioned that the method will diverge if the axial loading parameter l is larger than the corresponding critical value l cr.
APPENDIX - SOLUTION OF EXAMPLE 2.1 BY AN ENERGEY METHOD
Assuming that q1 and q2 are small (cos q1 = ![]() , cos q2 =
, cos q2 = ![]() and cose (q1-12) =
and cose (q1-12) = ![]() ) the potential energy of the system is given by
) the potential energy of the system is given by
V=U+W =![]() K1(2q1-q2)2 +
K1(2q1-q2)2 + ![]() K2 (2q1 - q1)2-
K2 (2q1 - q1)2-![]()
= (2 K1+![]() -P1)
-P1)![]() +
+![]() -(2 K1+2 K2-P1) q1-q2
-(2 K1+2 K2-P1) q1-q2
the conditions for a stationary potential energy ![]() = 0 and
= 0 and ![]() = 0 lead to the following system of equations, written in matrix form
= 0 lead to the following system of equations, written in matrix form
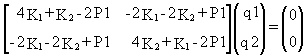
and to the corresponding iteration scheme is
K2 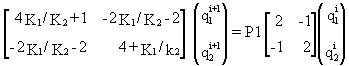
One should notice that this procedure always leads to a symmetric matrix, which was not that case in the previous solution. Obviously, both lead to the same results.